Optimization Toolbox のチュートリアル

ライブスクリプトを開く

このチュートリアルには、2 つの非線形最適化ソルバー (fminunc と fmincon) の使用方法とオプションの設定方法を示す複数の例が含まれています。このチュートリアルで紹介する原理は、fgoalattain、fminimax、lsqnonlin、lsqcurvefit、fsolve などの他の非線形ソルバーにも適用されます。

チュートリアルの例では以下のタスクを取り上げます。

目的関数の最小化
追加のパラメーターを使用した同じ関数の最小化
制約付きの目的関数の最小化
勾配またはヘッシアンを提供するか、オプションを変更することによる、より効率的または正確な解の取得

制約なしの最適化の例

次の関数の最小値を求める問題を考えます。

$x \exp (- (x^{2} + y^{2})) + (x^{2} + y^{2}) / 20 .$

関数をプロットしてそれが最小になる位置を確認します。

f = @(x,y) x.*exp(-x.^2-y.^2)+(x.^2+y.^2)/20;
fsurf(f,[-2,2],'ShowContours','on')

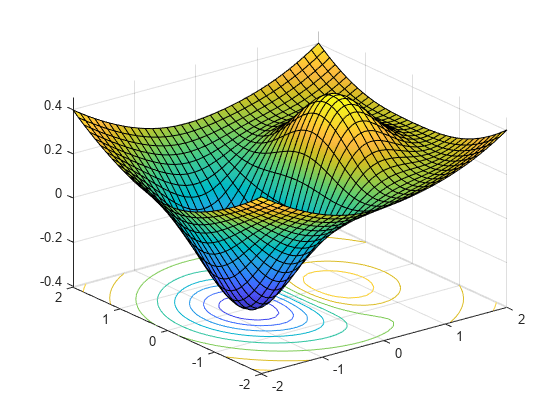
プロットは、最小値が点 (–1/2,0) の近くにあることを示しています。

通常は、目的関数を MATLAB® ファイルとして定義します。この場合は、関数が単純なため無名関数として定義します。

fun = @(x) f(x(1),x(2));

解を求める初期点を設定します。

x0 = [-.5; 0];

fminunc の既定の 'quasi-newton' アルゴリズムを使用するように最適化オプションを設定します。このステップにより、チュートリアルがすべての MATLAB バージョンで必ず同じように動作するようになります。

options = optimoptions('fminunc','Algorithm','quasi-newton');

ソルバーが計算を実行した反復回数を表示します。

options.Display = 'iter';

制約なしの非線形最小化関数 fminunc を呼び出します。

[x, fval, exitflag, output] = fminunc(fun,x0,options);

                                                        First-order 
 Iteration  Func-count       f(x)        Step-size       optimality
     0           3          -0.3769                         0.339
     1           6        -0.379694              1          0.286  
     2           9        -0.405023              1         0.0284  
     3          12        -0.405233              1        0.00386  
     4          15        -0.405237              1       3.17e-05  
     5          18        -0.405237              1       3.35e-08  

Local minimum found.

Optimization completed because the size of the gradient is less than
the value of the optimality tolerance.

ソルバーによって求められた解を表示します。

uncx = x

uncx = 2×1

   -0.6691
    0.0000

この解での関数値を表示します。

uncf = fval

uncf = -0.4052

この例では、関数評価の回数を効率の尺度として使用します。関数評価の合計回数を表示します。

output.funcCount

ans = 18

追加のパラメーターを使用した制約なしの最適化の例

ここでは、まず、MATLAB ファイルを使用して、次に、入れ子関数を使用して、特別なパラメーターを追加引数として目的関数に渡します。

前の例で示した目的関数を考えます。

$f (x, y) = x \exp (- (x^{2} + y^{2})) + (x^{2} + y^{2}) / 20 .$

次のように、(a,b,c) を使用して関数をパラメーター化します。

$f (x, y, a, b, c) = (x - a) \exp (- ((x - a)^{2} + (y - b)^{2})) + ((x - a)^{2} + (y - b)^{2}) / c .$

この関数は、元の目的関数をシフトおよびスケーリングしたバージョンです。

MATLAB ファイル関数

次のように定義された bowlpeakfun という名前の MATLAB ファイル目的関数を考えます。

type bowlpeakfun

function y = bowlpeakfun(x, a, b, c)
%BOWLPEAKFUN Objective function for parameter passing in TUTDEMO.

%   Copyright 2008 The MathWorks, Inc.

y = (x(1)-a).*exp(-((x(1)-a).^2+(x(2)-b).^2))+((x(1)-a).^2+(x(2)-b).^2)/c;

パラメーターを定義します。

a = 2;
b = 3;
c = 10;

MATLAB ファイルに対する無名関数ハンドルを作成します。

f = @(x)bowlpeakfun(x,a,b,c)

f = function_handle with value:
    @(x)bowlpeakfun(x,a,b,c)

fminunc を呼び出して、最小値を見つけます。

x0 = [-.5; 0];
options = optimoptions('fminunc','Algorithm','quasi-newton');
[x, fval] = fminunc(f,x0,options)

Local minimum found.

Optimization completed because the size of the gradient is less than
the value of the optimality tolerance.

fval = -0.3840

入れ子関数

目的を入れ子関数として実装する関数 nestedbowlpeak を考えます。

type nestedbowlpeak

function [x,fval] =  nestedbowlpeak(a,b,c,x0,options)
%NESTEDBOWLPEAK Nested function for parameter passing in TUTDEMO.

%   Copyright 2008 The MathWorks, Inc.

[x,fval] = fminunc(@nestedfun,x0,options);  
    function y = nestedfun(x)
      y = (x(1)-a).*exp(-((x(1)-a).^2+(x(2)-b).^2))+((x(1)-a).^2+(x(2)-b).^2)/c;    
    end
end

パラメーター (a,b,c) は入れ子目的関数 nestedfun に認識されます。外側の関数 nestedbowlpeak は fminunc を呼び出し、目的関数 nestedfun を渡します。

パラメーター、初期推定値、およびオプションを定義します。

a = 2;
b = 3;
c = 10;
x0 = [-.5; 0];
options = optimoptions('fminunc','Algorithm','quasi-newton');

最適化を実行します。

[x,fval] =  nestedbowlpeak(a,b,c,x0,options)

Local minimum found.

Optimization completed because the size of the gradient is less than
the value of the optimality tolerance.

fval = -0.3840

どちらのアプローチでも同じ結果が得られるため、都合の良い方を選択できます。

制約付き最適化の例: 不等式

前の問題を制約付きで考えます。

$minimize x \exp (- (x^{2} + y^{2})) + (x^{2} + y^{2}) / 20,$

$subject to x y / 2 + (x + 2)^{2} + (y - 2)^{2} / 2 \leq 2 .$

この制約は、傾いた楕円の内部です。傾いた楕円と一緒にプロットされた目的関数の等高線を表示します。

f = @(x,y) x.*exp(-x.^2-y.^2)+(x.^2+y.^2)/20;
g = @(x,y) x.*y/2+(x+2).^2+(y-2).^2/2-2;
fimplicit(g)
axis([-6 0 -1 7])
hold on
fcontour(f)
plot(-.9727,.4685,'ro');
legend('constraint','f contours','minimum');
hold off

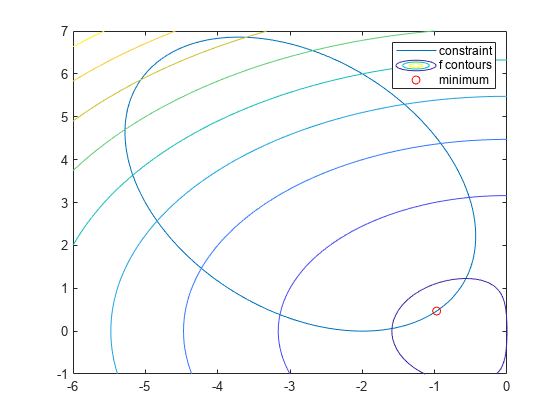
このプロットは、楕円内の目的関数の最小値が楕円の右下付近にあることを示しています。プロットされた最小値を計算する前に、その解を推定します。

x0 = [-2 1];

内点法アルゴリズムを使用して、反復ごとに結果を表示するように、最適化オプションを設定します。

options = optimoptions('fmincon','Algorithm','interior-point','Display','iter');

ソルバーには、非線形制約関数からの 2 つの出力が必要です。第 1 の出力は非線形不等式で、第 2 の出力は非線形等式です。両方の出力を提供するために、関数 deal を使用して制約を記述します。

gfun = @(x) deal(g(x(1),x(2)),[]);

非線形制約付きソルバーを呼び出します。問題に線形の等式、不等式、または範囲は含まれていないため、これらの引数として [ ] を渡します。

[x,fval,exitflag,output] = fmincon(fun,x0,[],[],[],[],[],[],gfun,options);

                                            First-order      Norm of
 Iter F-count            f(x)  Feasibility   optimality         step
    0       3    2.365241e-01    0.000e+00    1.972e-01
    1       6    1.748504e-01    0.000e+00    1.734e-01    2.260e-01
    2      10   -1.570560e-01    0.000e+00    2.608e-01    9.347e-01
    3      14   -6.629160e-02    0.000e+00    1.241e-01    3.103e-01
    4      17   -1.584082e-01    0.000e+00    7.934e-02    1.826e-01
    5      20   -2.349124e-01    0.000e+00    1.912e-02    1.571e-01
    6      23   -2.255299e-01    0.000e+00    1.955e-02    1.993e-02
    7      26   -2.444225e-01    0.000e+00    4.293e-03    3.821e-02
    8      29   -2.446931e-01    0.000e+00    8.100e-04    4.035e-03
    9      32   -2.446933e-01    0.000e+00    1.999e-04    8.126e-04
   10      35   -2.448531e-01    0.000e+00    4.004e-05    3.289e-04
   11      38   -2.448927e-01    0.000e+00    4.036e-07    8.156e-05

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

ソルバーによって求められた解を表示します。

x = 1×2

   -0.9727    0.4686

この解での関数値を表示します。

fval

fval = -0.2449

関数評価の合計回数を表示します。

Fevals = output.funcCount

Fevals = 38

不等式制約は、この解において満たされます。

[c, ceq] = gfun(x)

c = -2.4608e-06

ceq =

     []

c(x) が 0 に近いため、この制約は "アクティブ" です。つまり、解に影響を及ぼします。制約なしの解を再現します。

uncx

uncx = 2×1

   -0.6691
    0.0000

制約なしの目的関数を再現します。

uncf

uncf = -0.4052

制約によってどのくらい解が移動し、目的が増加したかを確認します。

fval-uncf

ans = 0.1603

制約付き最適化の例: 勾配を指定する場合

勾配を指定することによって、最適化問題をより効率的かつ正確に解くことができます。前の例と同様に、この例では、不等式制約付き問題を解きます。

$minimize x \exp (- (x^{2} + y^{2})) + (x^{2} + y^{2}) / 20,$

$subject to x y / 2 + (x + 2)^{2} + (y - 2)^{2} / 2 \leq 2 .$

f(x) の勾配を fmincon に与えるために、目的関数を MATLAB ファイルの形式で記述します。

type onehump

function [f,gf] = onehump(x)
% ONEHUMP Helper function for Tutorial for the Optimization Toolbox demo

%   Copyright 2008-2009 The MathWorks, Inc.

r = x(1)^2 + x(2)^2;
s = exp(-r);
f = x(1)*s+r/20;

if nargout > 1
   gf = [(1-2*x(1)^2)*s+x(1)/10;
       -2*x(1)*x(2)*s+x(2)/10];
end

制約とその勾配は、MATLAB ファイル tiltellipse に含まれています。

type tiltellipse

function [c,ceq,gc,gceq] = tiltellipse(x)
% TILTELLIPSE Helper function for Tutorial for the Optimization Toolbox demo

%   Copyright 2008-2009 The MathWorks, Inc.

c = x(1)*x(2)/2 + (x(1)+2)^2 + (x(2)-2)^2/2 - 2;
ceq = [];

if nargout > 2
   gc = [x(2)/2+2*(x(1)+2);
       x(1)/2+x(2)-2];
   gceq = [];
end

解を求める初期点を設定します。

x0 = [-2; 1];

比較のために前の例と同じアルゴリズムを使用するように最適化オプションを設定します。

options = optimoptions('fmincon','Algorithm','interior-point');

目的関数と制約関数で勾配情報を使用するようにオプションを設定します。メモ: これらのオプションは必ずオンにしてください。そうしないと、勾配情報が無視されます。

options = optimoptions(options,...
    'SpecifyObjectiveGradient',true,...
    'SpecifyConstraintGradient',true);

fmincon は有限差分を使用して勾配を推定する必要がないため、ソルバーの関数カウントが少なくなるはずです。反復ごとに結果を表示するようにオプションを設定します。

options.Display = 'iter';

ソルバーを呼び出します。

[x,fval,exitflag,output] = fmincon(@onehump,x0,[],[],[],[],[],[], ...
                                   @tiltellipse,options);

                                            First-order      Norm of
 Iter F-count            f(x)  Feasibility   optimality         step
    0       1    2.365241e-01    0.000e+00    1.972e-01
    1       2    1.748504e-01    0.000e+00    1.734e-01    2.260e-01
    2       4   -1.570560e-01    0.000e+00    2.608e-01    9.347e-01
    3       6   -6.629161e-02    0.000e+00    1.241e-01    3.103e-01
    4       7   -1.584082e-01    0.000e+00    7.934e-02    1.826e-01
    5       8   -2.349124e-01    0.000e+00    1.912e-02    1.571e-01
    6       9   -2.255299e-01    0.000e+00    1.955e-02    1.993e-02
    7      10   -2.444225e-01    0.000e+00    4.293e-03    3.821e-02
    8      11   -2.446931e-01    0.000e+00    8.100e-04    4.035e-03
    9      12   -2.446933e-01    0.000e+00    1.999e-04    8.126e-04
   10      13   -2.448531e-01    0.000e+00    4.004e-05    3.289e-04
   11      14   -2.448927e-01    0.000e+00    4.036e-07    8.156e-05

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

前の例で fmincon による勾配の推定が成功したため、この例での反復も同様です。

ソルバーによって求められた解を表示します。

xold = x

xold = 2×1

   -0.9727
    0.4686

この解での関数値を表示します。

minfval = fval

minfval = -0.2449

関数評価の合計回数を表示します。

Fgradevals = output.funcCount

Fgradevals = 14

この数字を、勾配を使用しない場合の関数評価回数と比較します。

Fevals

Fevals = 38

制約付き最適化の例: 既定の終了許容誤差の変更

この例では、勾配の使用に進んで、同じ制約付き問題を解きます。

$minimize x \exp (- (x^{2} + y^{2})) + (x^{2} + y^{2}) / 20,$

$subject to x y / 2 + (x + 2)^{2} + (y - 2)^{2} / 2 \leq 2$ .

この場合は、既定の終了基準 (options.StepTolerance と options.OptimalityTolerance) をオーバーライドすることによって、より正確な解を求めます。fmincon 内点法アルゴリズムの既定値は options.StepTolerance = 1e-10 と options.OptimalityTolerance = 1e-6 です。

この 2 つの既定の終了基準をオーバーライドします。

options = optimoptions(options,...
    'StepTolerance',1e-15,...
    'OptimalityTolerance',1e-8);

ソルバーを呼び出します。

[x,fval,exitflag,output] = fmincon(@onehump,x0,[],[],[],[],[],[], ...
                                   @tiltellipse,options);

                                            First-order      Norm of
 Iter F-count            f(x)  Feasibility   optimality         step
    0       1    2.365241e-01    0.000e+00    1.972e-01
    1       2    1.748504e-01    0.000e+00    1.734e-01    2.260e-01
    2       4   -1.570560e-01    0.000e+00    2.608e-01    9.347e-01
    3       6   -6.629161e-02    0.000e+00    1.241e-01    3.103e-01
    4       7   -1.584082e-01    0.000e+00    7.934e-02    1.826e-01
    5       8   -2.349124e-01    0.000e+00    1.912e-02    1.571e-01
    6       9   -2.255299e-01    0.000e+00    1.955e-02    1.993e-02
    7      10   -2.444225e-01    0.000e+00    4.293e-03    3.821e-02
    8      11   -2.446931e-01    0.000e+00    8.100e-04    4.035e-03
    9      12   -2.446933e-01    0.000e+00    1.999e-04    8.126e-04
   10      13   -2.448531e-01    0.000e+00    4.004e-05    3.289e-04
   11      14   -2.448927e-01    0.000e+00    4.036e-07    8.156e-05
   12      15   -2.448931e-01    0.000e+00    4.000e-09    8.230e-07

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

新しい許容誤差によって生じる差をより正確に把握するために、解の小数点以下の桁数を増やします。

format long

ソルバーによって求められた解を表示します。

x = 2×1

  -0.972742227363546
   0.468569289098342

これらの値と前の例の値を比較します。

xold

xold = 2×1

  -0.972742694488360
   0.468569966693330

値の違いを確認します。

x - xold

ans = 2×1
10^-6 ×

   0.467124813385844
  -0.677594988729435

この解での関数値を表示します。

fval

fval = 
  -0.244893137879894

解がどのくらい改善したかを確認します。

fval - minfval

ans = 
    -3.996450220755676e-07

新しい解の方が小さいため、答えは負になります。

関数評価の合計回数を表示します。

output.funcCount

ans = 
    15

この数字を、ユーザー指定の勾配と既定の許容誤差を使用して解いた例の関数評価の回数と比較します。

Fgradevals

Fgradevals = 
    14

制約付き最適化の例: ユーザー指定のヘッシアン

勾配だけでなくヘッシアンも指定すると、ソルバーの精度と効率がさらに向上します。

fmincon 内点法アルゴリズムは、ヘッセ行列を別個の関数 (目的関数の一部ではなく) として取得します。ヘッセ関数 H(x,lambda) は、ラグランジュ関数のヘッシアンを評価します。fmincon の内点法アルゴリズムのヘッシアンを参照してください。

ソルバーが、値の lambda.ineqnonlin と lambda.eqlin を計算します。ヘッセ関数が、これらの値の使用方法をソルバーに指示します。

この例には不等式制約が 1 つしか含まれていないため、ヘッシアンは関数 hessfordemo で指定されたように定義されます。

type hessfordemo

function H = hessfordemo(x,lambda)
% HESSFORDEMO Helper function for Tutorial for the Optimization Toolbox demo

%   Copyright 2008-2009 The MathWorks, Inc.

s = exp(-(x(1)^2+x(2)^2));
H = [2*x(1)*(2*x(1)^2-3)*s+1/10, 2*x(2)*(2*x(1)^2-1)*s;
        2*x(2)*(2*x(1)^2-1)*s, 2*x(1)*(2*x(2)^2-1)*s+1/10];
hessc = [2,1/2;1/2,1];
H = H + lambda.ineqnonlin(1)*hessc;

このヘッシアンを使用するには、オプションを適切に設定しなければなりません。

options = optimoptions('fmincon',...
    'Algorithm','interior-point',...
    'SpecifyConstraintGradient',true,...
    'SpecifyObjectiveGradient',true,...
    'HessianFcn',@hessfordemo);

許容誤差は既定値に設定されるため、関数カウントは減るはずです。反復ごとに結果を表示するようにオプションを設定します。

options.Display = 'iter';

ソルバーを呼び出します。

[x,fval,exitflag,output] = fmincon(@onehump,x0,[],[],[],[],[],[], ...
                                   @tiltellipse,options);

                                            First-order      Norm of
 Iter F-count            f(x)  Feasibility   optimality         step
    0       1    2.365241e-01    0.000e+00    1.972e-01
    1       3    5.821325e-02    0.000e+00    1.443e-01    8.728e-01
    2       5   -1.218829e-01    0.000e+00    1.007e-01    4.927e-01
    3       6   -1.421167e-01    0.000e+00    8.486e-02    5.165e-02
    4       7   -2.261916e-01    0.000e+00    1.989e-02    1.667e-01
    5       8   -2.433609e-01    0.000e+00    1.537e-03    3.486e-02
    6       9   -2.446875e-01    0.000e+00    2.057e-04    2.727e-03
    7      10   -2.448911e-01    0.000e+00    2.068e-06    4.191e-04
    8      11   -2.448931e-01    0.000e+00    2.001e-08    4.218e-06

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

結果は、反復回数が少なくなり、異なる反復が示されます。

ソルバーによって求められた解を表示します。

x = 2×1

  -0.972742246093537
   0.468569316215571

この解での関数値を表示します。

fval

fval = 
  -0.244893121872758

関数評価の合計回数を表示します。

output.funcCount

ans = 
    11

この数字を、既定の許容誤差を同じにし、勾配評価のみを使用して解いた例の関数評価の回数と比較します。

Fgradevals

Fgradevals = 
    14

Optimization Toolbox のチュートリアル

制約なしの最適化の例

追加のパラメーターを使用した制約なしの最適化の例

MATLAB ファイル関数

入れ子関数

制約付き最適化の例: 不等式

制約付き最適化の例: 勾配を指定する場合

制約付き最適化の例: 既定の終了許容誤差の変更

制約付き最適化の例: ユーザー指定のヘッシアン

関連するトピック