fmincon ソルバーを使用した最適化ライブ エディター タスク
この例では、線形と非線形の制約と範囲をもつ二次式を最小化するために、[fmincon] ソルバーと共にソルバーベースの [最適化] ライブ エディター タスクを使用する方法を示します。
以下を解く、[x1, x2] を探す問題を考えてみましょう。
以下の制約に従います。
この問題の開始点 x0 は、x1 = 3 と x2 = 1 です。
最適化ライブ エディター タスクの開始
[ホーム] タブの [ファイル] セクションで [新規ライブ スクリプト] ボタンをクリックして、新しいライブ スクリプトを作成します。

[最適化] ライブ エディター タスクを挿入します。[挿入] タブをクリックしてから、[コード] セクションで、[タスク]、[最適化] を選択します。


この例の場合は、ソルバーベースのタスクを選択します。

後で問題データの入力で使用するために、[挿入]、[セクション区切り] を選択します。新しいセクションがタスクの上と下に表示されます。
問題のデータの入力
タスクの一番上から、問題タイプと制約タイプを入力します。[目的]、[2 次] ボタンと、[制約]、[下限]、[線形不等式]、および [非線形] の各ボタンをクリックします。推奨ソルバーは
fminconであると表示されます。目的関数
目的関数は、十分単純なため、無名関数として表現できます。カーソルをタスクの上のセクションに配置して、次のコードを入力します。
fun = @(x)sum(x.^2);
下限
問題には、下限 x1 ≥ 0.5 が含まれています。この範囲を変数
lbで表します。カーソルを目的関数を定義する行の末尾に配置して、Enter を押し、下限を指定する次のコードを入力します。lb = [0.5 -Inf];
初期点
カーソルを下限を定義する行の末尾に配置して、Enter を押し、初期点を設定する次のコードを入力します。
x0 = [3,1];
線形制約
カーソルを初期点を定義する行の末尾に配置して、Enter を押し、線形制約を設定する次のコードを入力します。
A = [-1,-1]; b = -1;
セクションの実行
これで、一番上のセクションに 5 つのパラメーターが表示されます。
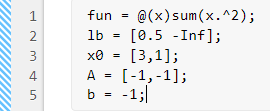
次に、セクションを実行して、パラメーターをワークスペースに変数として配置する必要があります。これを行うには、斜めの縞模様のバーを含む、セクションの左端の領域をクリックします。この領域をクリックすると、バーが無地のバーになり、変数がワークスペースに配置されたことが示されます (メモ:Ctrl+Enter を押して、セクションを実行することもできます)。
問題データの設定
タスクの [問題のデータの選択] セクションに変数を入力します。目的関数を指定するために、[目的関数]、[関数ハンドル] を選択して、[fun] を選択します。
初期点 [x0] を設定します。
[下限]、[From workspace] を選択して、[lb] を選択します。
[線形不等式] 領域で、線形不等式制約変数の
Aとbを設定します。ここで、非線形不等式制約を指定します。[問題のデータの選択] セクションで、[非線形]、[ローカル関数] を選択してから、[新規] ボタンをクリックします。タスクの下側の新しいセクションに関数が表示されます。以下のコメントが解除された行を含むように生成されたコードを編集します。
function [c,ceq] = constraintFcn(x) % You can include commented code lines or not. % Be sure that just these uncommented lines remain: c = [-x(1)^2 - x(2)^2 + 1; -9*x(1)^2 - x(2)^2 + 9; -x(1)^2 + x(2); -x(2)^2 + x(1)]; ceq = []; end
[問題のデータの選択] セクションで、[constraintFcn] を選択します。
進行状況の監視
タスクの [進行状況の表示] セクションで、[テキスト表示]、[各反復] を選択して、ソルバーの進行状況を監視できるようにします。プロットの [目的値] を選択します。
設定は次のようになります。

ソルバーの実行と結果の検証
ソルバーを実行するには、タスク ウィンドウの右上にあるオプション ボタン [⁝] をクリックして、[セクションの実行] を選択します。

別の Figure ウィンドウとタスク出力領域にプロットが表示されます。
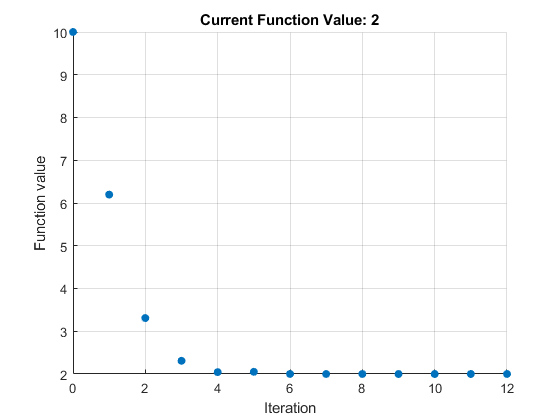
解の変数が返された場所を見つけるには、タスクの一番上を確認します。
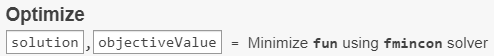
最終点とその関連目的関数値が、ワークスペースの solution 変数と objectiveValue 変数に表示されます。これらの値は、次のコードをタスクの下のライブ エディター セクションに入力することによって表示されます。
solution, objectiveValue
Ctrl+Enter を押して、セクションを実行します。
![solution = [1 1], objectiveValue = 2](optimizelet_fmincon_answer.png)