最良実行可能点の取得
この例では、fmincon で見つかる最良実行可能点の取得方法を示します。
補助関数 bigtoleft は、x(1) 座標が負になるほど急速に負になる 3 次元変数 x 内の 3 次多項式目的関数です。その勾配は 3 要素のベクトルです。補助関数 bigtoleft のコードは、この例の終わりに掲載しています。
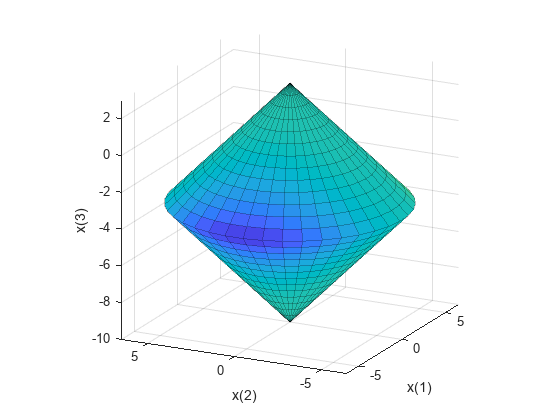
この例の制約集合は 2 つの円錐の内部交差部分です。1 つの円錐は上向きで、もう 1 つの円錐は下向きです。制約関数は各円錐に対して 1 つの要素を含む 2 要素のベクトルです。この例は 3 次元であるため、制約の勾配は 3 行 2 列の行列です。補助関数 twocone のコードは、この例の終わりに掲載しています。
目的関数を使用して関数 plottwoconecons を呼び出すことによって色分けされた制約の Figure を作成します (この例の最後にコードが掲載されています)。
figure1 = plottwoconecons;
導関数を使用するためのオプションの作成
fmincon で目的勾配と制約勾配を使用できるようにするために、適切なオプションを設定します。"sqp" アルゴリズムを選択します。
options = optimoptions("fmincon",Algorithm="sqp",... SpecifyConstraintGradient=true,SpecifyObjectiveGradient=true);
解法プロセスを検証するために、反復表示を返すようにオプションを設定します。
options.Display = "iter";導関数情報を使用した最小化
初期点 x0 = [-1/20,-1/20,-1/20] を設定します。
x0 = -1/20*ones(1,3);
この問題には、線形制約または範囲がありません。これらの引数を [] に設定します。
A = []; b = []; Aeq = []; beq = []; lb = []; ub = [];
問題を解きます。
[x,fval,eflag,output] = fmincon(@bigtoleft,x0,...
A,b,Aeq,beq,lb,ub,@twocone,options); Iter Func-count Fval Feasibility Step Length Norm of First-order
step optimality
0 1 -1.625000e-03 0.000e+00 1.000e+00 0.000e+00 8.250e-02
1 3 -2.490263e-02 0.000e+00 1.000e+00 8.325e-02 5.449e-01
2 5 -2.529919e+02 0.000e+00 1.000e+00 2.802e+00 2.585e+02
3 7 -6.408576e+03 9.472e+00 1.000e+00 1.538e+01 1.771e+03
4 9 -1.743599e+06 5.301e+01 1.000e+00 5.991e+01 9.216e+04
5 11 -5.552305e+09 1.893e+03 1.000e+00 1.900e+03 1.761e+07
6 13 -1.462524e+15 5.632e+04 1.000e+00 5.636e+04 8.284e+10
7 15 -2.573346e+24 1.471e+08 1.000e+00 1.471e+08 1.058e+17
8 17 -1.467510e+41 2.617e+13 1.000e+00 2.617e+13 1.789e+28
9 19 -8.716877e+72 2.210e+24 1.000e+00 2.210e+24 2.387e+49
10 21 -2.426511e+135 8.214e+44 1.000e+00 6.596e+44 1.167e+91
11 23 -4.721413e+258 9.223e+85 1.000e+00 8.703e+85 1.806e+173
Objective function returned NaN; trying a new point...
12 300 -4.721413e+258 9.223e+85 1.766e-43 4.785e+141 1.806e+173
Feasible point with lower objective function value found, but optimality criteria not satisfied. See output.bestfeasible..
Solver stopped prematurely.
fmincon stopped because it exceeded the function evaluation limit,
options.MaxFunctionEvaluations = 3.000000e+02.
解および解法プロセスの検証
解、目的関数値、終了フラグおよび関数評価と反復の回数を調べます。
disp(x)
1.0e+85 * -7.7428 3.9370 0.5363
disp(fval)
-4.7214e+258
disp(eflag)
0
disp(output.constrviolation)
9.2225e+85
目的関数値は、非常に大きな負の値である –1e250 より小さくなります。制約違反は 1e85 を超えています。これは大きな値ですが、それでも目的関数値よりはるかに小さな値です。終了フラグも、返された解が実行不可能であることを示しています。
目的関数値と一緒に、fmincon で見つかる最良実行可能点を回復するために、output.bestfeasible 構造体を表示します。
disp(output.bestfeasible)
x: [-2.9297 -0.1813 -0.1652]
fval: -252.9919
constrviolation: 0
firstorderopt: 258.5032
bestfeasible 点は、次のセクションで確認するように、適切な解ではありません。これは、fmincon の反復で見つかった最良実行可能点にすぎません。この場合、bestfeasible は解ではありませんが、返された実行不可能な解よりは適切な点です。
table([fval;output.bestfeasible.fval],... [output.constrviolation;output.bestfeasible.constrviolation],... VariableNames=["Fval" "Constraint Violation"],... RowNames=["Final Point" "Best Feasible"])
ans=2×2 table
Fval Constraint Violation
____________ ____________________
Final Point -4.7214e+258 9.2225e+85
Best Feasible -252.99 0
output.bestfeasible 構造体には、fmincon の反復が終了するたびに見つかった最良実行可能点が含まれます。まれに、fmincon の中間の計算で、報告よりもさらに低い目的関数値をもつ実行可能点が見つかる可能性があります。
解の改善:範囲の設定
実行可能解を取得する方法は複数あります。1 つは変数で範囲を設定する方法です。
lb = -10*ones(3,1);
ub = -lb;
[xb,fvalb,eflagb,outputb] = fmincon(@bigtoleft,x0,...
A,b,Aeq,beq,lb,ub,@twocone,options); Iter Func-count Fval Feasibility Step Length Norm of First-order
step optimality
0 1 -1.625000e-03 0.000e+00 1.000e+00 0.000e+00 8.250e-02
1 3 -2.490263e-02 0.000e+00 1.000e+00 8.325e-02 5.449e-01
2 5 -2.529919e+02 0.000e+00 1.000e+00 2.802e+00 2.585e+02
3 7 -4.867942e+03 5.782e+00 1.000e+00 1.151e+01 1.525e+03
4 9 -1.035980e+04 3.536e+00 1.000e+00 9.587e+00 1.387e+03
5 12 -5.270030e+03 2.143e+00 7.000e-01 4.865e+00 2.804e+02
6 14 -2.538935e+03 2.855e-02 1.000e+00 2.229e+00 1.715e+03
7 16 -2.703318e+03 2.331e-02 1.000e+00 5.517e-01 2.521e+02
8 19 -2.845097e+03 0.000e+00 1.000e+00 1.752e+00 8.874e+01
9 21 -2.896933e+03 2.149e-03 1.000e+00 1.709e-01 1.608e+01
10 23 -2.894135e+03 7.953e-06 1.000e+00 1.039e-02 2.028e+00
11 25 -2.894126e+03 4.114e-07 1.000e+00 2.313e-03 2.100e-01
12 27 -2.894125e+03 4.618e-09 1.000e+00 2.450e-04 1.470e-04
Feasible point with lower objective function value found, but optimality criteria not satisfied. See output.bestfeasible..
Local minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.
<stopping criteria details>
反復表示は、fmincon が実行可能点 (実行可能性 0) で開始して、数回の実行不可能な反復を消費し、再び 0 実行可能性に戻ってから、残りの反復で小さいものの非ゼロの実行不可能性に到達することを示しています。ソルバーも、最終点 xb 以外の点でより小さい実行可能値を発見したことを再度報告します。最終点と目的関数値、および目的関数値がより低い報告された実行可能点を表示します。
disp(xb)
-6.5000 -0.0000 -3.5000
disp(fvalb)
-2.8941e+03
disp(outputb.bestfeasible)
x: [-6.5000 2.4498e-04 -3.5000]
fval: -2.8941e+03
constrviolation: 4.1139e-07
firstorderopt: 0.2100
bestfeasible 点での制約違反は約 4.113e-7 です。反復表示では、この実行不可能性が反復 11 で発生します。その反復で報告された目的関数値は、-2.894126e3 で、-2.894125e3 の最終値よりわずかに小さいです。最終点は、実行不可能性がより低く、1 次の最適性の尺度です。どちらの点がより適切でしょうか。これらはほぼ同じですが、それぞれに一方の点より優れた点があります。解の詳細を確認するために、表示形式を long に設定します。
format long table([fvalb;outputb.bestfeasible.fval],... [outputb.constrviolation;outputb.bestfeasible.constrviolation],... [outputb.firstorderopt;outputb.bestfeasible.firstorderopt],... VariableNames=["Function Value" "Constraint Violation" "First-Order Optimality"],... RowNames=["Final Point" "Best Feasible"])
ans=2×3 table
Function Value Constraint Violation First-Order Optimality
_________________ ____________________ ______________________
Final Point -2894.12500606352 4.61806859419767e-09 0.000146960595316159
Best Feasible -2894.12553469474 4.11390739252226e-07 0.210026484000832
解の改善:別のアルゴリズムの使用
実行可能解を取得する別の方法は、境界のない "interior-point" アルゴリズムを使用する方法です。
lb = []; ub = []; options.Algorithm = "interior-point"; [xip,fvalip,eflagip,outputip] = fmincon(@bigtoleft,x0,... A,b,Aeq,beq,lb,ub,@twocone,options);
First-order Norm of
Iter F-count f(x) Feasibility optimality step
0 1 -1.625000e-03 0.000e+00 7.807e-02
1 2 -2.374253e-02 0.000e+00 5.222e-01 8.101e-02
2 3 -2.232989e+02 0.000e+00 2.379e+02 2.684e+00
3 4 -3.838433e+02 1.768e-01 3.198e+02 5.573e-01
4 5 -3.115565e+03 1.810e-01 1.028e+03 4.660e+00
5 6 -3.143463e+03 2.013e-01 8.965e+01 5.734e-01
6 7 -2.917730e+03 1.795e-02 6.140e+01 5.231e-01
7 8 -2.894095e+03 0.000e+00 9.206e+00 1.821e-02
8 9 -2.894107e+03 0.000e+00 2.500e+00 3.899e-03
9 10 -2.894142e+03 1.299e-05 2.136e-03 1.371e-02
10 11 -2.894125e+03 3.614e-08 4.070e-03 1.739e-05
11 12 -2.894125e+03 0.000e+00 5.994e-06 5.832e-08
Feasible point with lower objective function value found, but optimality criteria not satisfied. See output.bestfeasible..
Local minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.
<stopping criteria details>
反復表示は、fmincon が解の検索時点で実行不可能な点に到達し、fmincon が目的関数値がより低い実行可能点を発見したというメッセージを再度発行したことを示しています。
disp(xip)
-6.499999996950366 -0.000000032933162 -3.500000000098132
disp(fvalip)
-2.894124995999976e+03
disp(outputip.bestfeasible)
x: [-6.500000035892771 -7.634107877056255e-08 -3.500000000245461]
fval: -2.894125047137579e+03
constrviolation: 3.613823285064655e-08
firstorderopt: 0.004069724066085
ここでも 2 つの解はほぼ同じですが、bestfeasible 解は終了前の反復で出力されます。最終解 xip のほうが 1 次の最適性の尺度と実行可能性が優れていますが、bestfeasible 解のほうが目的関数値がわずかに小さく、実現不可能性はあまり大きくありません。
table([fvalip;outputip.bestfeasible.fval],... [outputip.constrviolation;outputip.bestfeasible.constrviolation],... [outputip.firstorderopt;outputip.bestfeasible.firstorderopt],... VariableNames=["Function Value" "Constraint Violation" "First-Order Optimality"],... RowNames=["Final Point" "Best Feasible"])
ans=2×3 table
Function Value Constraint Violation First-Order Optimality
_________________ ____________________ ______________________
Final Point -2894.12499599998 0 5.99383553128062e-06
Best Feasible -2894.12504713758 3.61382328506465e-08 0.00406972406608475
最後に、形式を既定の short に戻します。
format short補助関数
次のコードは、bigtoleft 補助関数を作成します。
function [f,gradf] = bigtoleft(x) % This is a simple function that grows rapidly negative % as x(1) becomes negative. % f = 10*x(:,1).^3 + x(:,1).*x(:,2).^2 + x(:,3).*(x(:,1).^2 + x(:,2).^2); if nargout > 1 gradf=[30*x(1)^2+x(2)^2+2*x(3)*x(1); 2*x(1)*x(2)+2*x(3)*x(2); (x(1)^2+x(2)^2)]; end end
次のコードは、twocone 補助関数を作成します。
function [ineqnonlin,eqnonlin,gradineqnonlin,gradeqnonlin] = twocone(x) % This constraint is two cones, z > -10 + r % and z < 3 - r. eqnonlin = []; r = sqrt(x(1)^2 + x(2)^2); ineqnonlin = [-10+r-x(3); x(3)-3+r]; if nargout > 2 gradeqnonlin = []; gradineqnonlin = [x(1)/r,x(1)/r; x(2)/r,x(2)/r; -1,1]; end end
このコードは、非線形制約をプロットする関数を作成します。
function figure1 = plottwoconecons % Create figure figure1 = figure; % Create axes axes1 = axes(Parent=figure1); view([-63.5 18]); grid("on"); hold("on"); % Set up polar coordinates and two cones r = linspace(0,6.5,14); th = 2*pi*linspace(0,1,40); x = r'*cos(th); y = r'*sin(th); z = -10+sqrt(x.^2+y.^2); zz = 3-sqrt(x.^2+y.^2); % Evaluate objective function on cone surfaces newxf = reshape(bigtoleft([x(:),y(:),z(:)]),14,40)/3000; newxg = reshape(bigtoleft([x(:),y(:),z(:)]),14,40)/3000; % Create lower surf with color set by objective surf(x,y,z,newxf,Parent=axes1,EdgeAlpha=0.25); % Create upper surf with color set by objective surf(x,y,zz,newxg,Parent=axes1,EdgeAlpha=0.25); axis equal xlabel "x(1)" ylabel "x(2)" zlabel "x(3)" end
