勾配およびヘッセスパースパターンを使った最小化

この例では、明示的な計算の代わりにスパース有限差分で近似された三重対角ヘッセ行列を使用して非線形最小化問題を解く方法を説明します。

この問題は以下を最小化する $x$ を見つけるものです。

$f (x) = \sum_{i = 1}^{n - 1} ({(x_{i}^{2})}^{(x_{i + 1}^{2} + 1)} + {(x_{i + 1}^{2})}^{(x_{i}^{2} + 1)}),$

ここで $n$ = 1000 です。

n = 1000;

fminunc で trust-region メソッドを使用するには、目的関数の勾配を計算しなければなりません。これは quasi-newton メソッドとは異なり、オプションではありません。

補助関数 brownfg (この例の終わりに掲載) が、目的関数と勾配を計算します。

ヘッセ行列 $H (x)$ のスパース有限差分近似の計算を効率的に行うために、 $H$ のスパース構造を事前に決めておかなければなりません。ここでは、スパース行列である構造体 Hstr が、ファイル brownhstr.mat で利用可能とします。spy コマンドを使用すると、Hstr がスパースであること (非ゼロは 2998 個のみ) を確認することができます。

load brownhstr
spy(Hstr)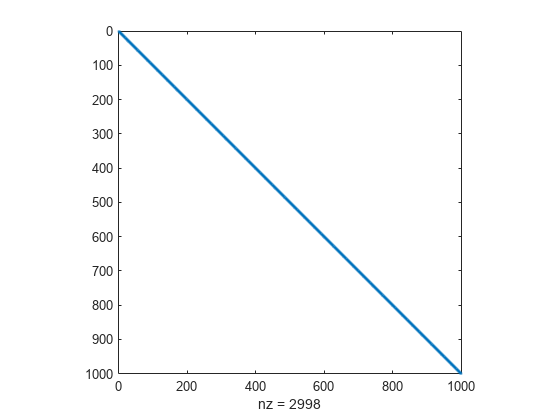

Figure contains an axes object. The axes object contains an object of type line.

optimoptions を使用して HessPattern オプションを Hstr に設定します。このような大きな問題が明らかにスパース構造をもつ場合、HessPattern オプションを設定しないと、fminunc は 100 万の非ゼロ要素をもつ非スパースなヘッセ行列に有限差分を使おうとするため、不必要に膨大なメモリと計算量を使用します。

ヘッセスパースパターンを使用するには、fminunc の trust-region アルゴリズムを使用しなければなりません。このアルゴリズムにおいても optimoptions を使用して、SpecifyObjectiveGradient オプションを true に設定する必要があります。

options = optimoptions(@fminunc,'Algorithm','trust-region',...
    'SpecifyObjectiveGradient',true,'HessPattern',Hstr);

目的関数を @brownfg に設定します。初期点として奇数の $x$ 要素に対して -1 を設定し、偶数の $x$ 要素に対して +1 を設定します。

xstart = -ones(n,1); 
xstart(2:2:n,1) = 1;
fun = @brownfg;

初期点 xstart およびオプション options を使用して fminunc を呼び出し、問題を解きます。

[x,fval,exitflag,output] = fminunc(fun,xstart,options);

Local minimum found.

Optimization completed because the size of the gradient is less than
the value of the optimality tolerance.

解法および解法プロセスを検証します。

disp(fval)

   7.4738e-17

disp(exitflag)

disp(output)

         iterations: 7
          funcCount: 8
           stepsize: 0.0046
       cgiterations: 7
      firstorderopt: 7.9822e-10
          algorithm: 'trust-region'
            message: 'Local minimum found....'
    constrviolation: []

関数 $f (x)$ は、二乗の和であるため、非負となります。解 fval はほぼゼロであるため、最小値であることは明らかです。終了フラグが 1 であることも fminunc が解を見つけたことを示しています。output 構造体は、fminunc がわずか 7 回の反復で解に到達したことを示しています。

解の最大要素と最小要素を表示します。

disp(max(x))

   1.9955e-10

disp(min(x))

  -1.9955e-10

この解は、すべての要素が x = 0 となる点に近いものとなります。

補助関数

次のコードは、補助関数 brownfg を作成します。

function [f,g] = brownfg(x)
% BROWNFG Nonlinear minimization test problem
% 
% Evaluate the function
n=length(x); y=zeros(n,1);
i=1:(n-1);
y(i)=(x(i).^2).^(x(i+1).^2+1) + ...
        (x(i+1).^2).^(x(i).^2+1);
  f=sum(y);
% Evaluate the gradient if nargout > 1
  if nargout > 1
     i=1:(n-1); g = zeros(n,1);
     g(i) = 2*(x(i+1).^2+1).*x(i).* ...
              ((x(i).^2).^(x(i+1).^2))+ ...
              2*x(i).*((x(i+1).^2).^(x(i).^2+1)).* ...
              log(x(i+1).^2);
     g(i+1) = g(i+1) + ...
              2*x(i+1).*((x(i).^2).^(x(i+1).^2+1)).* ...
              log(x(i).^2) + ...
              2*(x(i).^2+1).*x(i+1).* ...
              ((x(i+1).^2).^(x(i).^2));
  end
end

勾配およびヘッセ スパース パターンを使った最小化

補助関数

関連するトピック

勾配およびヘッセスパースパターンを使った最小化