範囲制約および範囲付きの前提条件子を使った最小化

ライブスクリプトを開く

この例では、fmincon trust-region-reflective アルゴリズムを使用して、範囲のある非線形問題を解く方法を説明します。このアルゴリズムは、問題がスパースである場合に効率性を高める効果があり、解析勾配、およびヘッシアンのパターンなどの既知の構造を備えています。

勾配のある目的関数

与えられた $n$ が 4 の倍数である正の数のとき、目的関数は次のようになります。

$f (x) = 1 + \sum_{i = 1}^{n} {| (3 - 2 x_{i}) x_{i} - x_{i - 1} - x_{i + 1} + 1 |}^{p} + \sum_{i = 1}^{n / 2} {| x_{i} + x_{i + n / 2} |}^{p},$

ここで、 $p = 7 / 3$ 、 $x_{0} = 0$ 、および $x_{n + 1} = 0$ です。補助関数 tbroyfg (この例の終わりに掲載) は、その勾配を含む目的関数を実装するものです。

この問題では、すべての $i$ について $- 10 \leq x_{i} \leq 10$ という範囲があります。 $n$ = 800 を使用します。

n = 800;
lb = -10*ones(n,1);
ub = -lb;

ヘッシアンのパターン

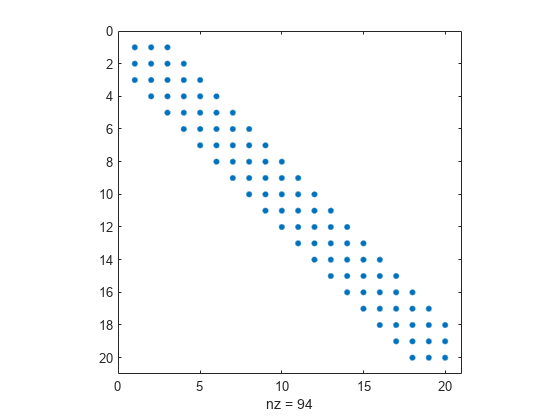
ヘッセ行列のスパースパターンは事前定義され、ファイル tbroyhstr.mat に保存されています。この問題のヘッシアンに関するスパース構造は、次の spy プロットのように縞模様になっています。

load tbroyhstr
spy(Hstr)

Figure contains an axes object. The axes object contains an object of type line.

このプロットでは、中央のストライプは、5 つの縞模様の行列です。以下のプロットは、行列をより明示的に示します。

spy(Hstr(1:20,1:20))

Figure contains an axes object. The axes object contains an object of type line.

問題のオプション

trust-region-reflective アルゴリズムを使用するためのオプションを設定します。このアルゴリズムでは、SpecifyObjectiveGradient オプションを true に設定する必要があります。

また、optimoptions を使用して HessPattern オプションを Hstr に設定してください。このような大きな問題が明らかにスパース構造をもつ場合、このオプションを設定しないと、fmincon は 64 万の非ゼロ要素をもつ非スパースなヘッセ行列に有限差分を使おうとするため、膨大なメモリと計算を使用します。

options = optimoptions('fmincon','SpecifyObjectiveGradient',true,'HessPattern',Hstr,...
    'Algorithm','trust-region-reflective');

問題を解く

初期点として奇数インデックスに対して -1 を設定し、偶数インデックスに対して +1 を設定します。

x0 = -ones(n,1);
x0(2:2:n) = 1;

この問題には線形制約または非線形制約がないため、これらのパラメーターを [] に設定します。

A = [];
b = [];
Aeq = [];
beq = [];
nonlcon = [];

fmincon を呼び出してこの問題を解きます。

[x,fval,exitflag,output] = ... 
   fmincon(@tbroyfg,x0,A,b,Aeq,beq,lb,ub,nonlcon,options);

Local minimum possible.

fmincon stopped because the final change in function value relative to 
its initial value is less than the value of the function tolerance.

解および解法プロセスの検証

終了フラグ、目的関数値、1 次の最適性の尺度、およびソルバーの反復回数を検証します。

disp(exitflag);

disp(fval)

  270.4790

disp(output.firstorderopt)

    0.0163

disp(output.iterations)

fmincon が解に到達するまでの反復回数は、それほど多くはありません。ただし、この解は 1 次の最適性の尺度が比較的高いため、終了フラグは望ましい値である 1 ではありません。

解の改善

既定の対角型の前提条件子の代わりに、5 つの縞模様の前提条件子を使用してみてください。optimoptions を使用し、PrecondBandWidth オプションを 2 に設定して、再度問題を解きます。(帯域幅は、主対角をカウントせず、上または下対角の数です。)

options.PrecondBandWidth = 2;
[x2,fval2,exitflag2,output2] = ... 
   fmincon(@tbroyfg,x0,A,b,Aeq,beq,lb,ub,nonlcon,options);

Local minimum possible.

fmincon stopped because the final change in function value relative to 
its initial value is less than the value of the function tolerance.

disp(exitflag2);

disp(fval2)

  270.4790

disp(output2.firstorderopt)

   7.5340e-05

disp(output2.iterations)

終了フラグと目的関数値に変化は見られません。ただし、反復回数は増加し、1 次の最適性の尺度は大幅に減少します。目的関数値の差を計算します。

disp(fval2 - fval)

  -2.9005e-07

目的関数値は少ししか減少していません。解が主に改善しているのは、目的関数ではなく、1 次の最適性の尺度です。

補助関数

次のコードは、補助関数 tbroyfg を作成します。

function [f,grad] = tbroyfg(x,dummy)
%TBROYFG Objective function and its gradients for nonlinear minimization
% with bound constraints and banded preconditioner.
% Documentation example.

%   Copyright 1990-2008 The MathWorks, Inc.

n = length(x);  % n should be a multiple of 4
p = 7/3;
y=zeros(n,1);
i = 2:(n-1);
y(i) = abs((3-2*x(i)).*x(i) - x(i-1) - x(i+1)+1).^p;
y(n) = abs((3-2*x(n)).*x(n) - x(n-1)+1).^p;
y(1) = abs((3-2*x(1)).*x(1) - x(2)+1).^p;
j = 1:(n/2);
z = zeros(length(j),1);
z(j) = abs(x(j) + x(j+n/2)).^p;
f = 1 + sum(y) + sum(z);
%
% Evaluate the gradient.
if nargout > 1
   g = zeros(n,1);
   t = zeros(n,1);
   i = 2:(n-1);
   t(i) = (3-2*x(i)).*x(i) - x(i-1) - x(i+1) + 1;
   g(i) = p*abs(t(i)).^(p-1).*sign(t(i)).*(3-4*x(i));
   g(i-1) = g(i-1) - p*abs(t(i)).^(p-1).*sign(t(i));
   g(i+1) = g(i+1) - p*abs(t(i)).^(p-1).*sign(t(i));
   tt = (3-2*x(n)).*x(n) - x(n-1) + 1;
   g(n) = g(n) + p*abs(tt).^(p-1).*sign(tt).*(3-4*x(n));
   g(n-1) = g(n-1) - p*abs(tt).^(p-1).*sign(tt);
   tt = (3-2*x(1)).*x(1)-x(2)+1;
   g(1) = g(1) + p*abs(tt).^(p-1).*sign(tt).*(3-4*x(1));
   g(2) = g(2) - p*abs(tt).^(p-1).*sign(tt);
   j = 1:(n/2);
   t(j) = x(j) + x(j+n/2);
   g(j) = g(j) + p*abs(t(j)).^(p-1).*sign(t(j));
   jj = j + (n/2);
   g(jj) = g(jj) + p*abs(t(j)).^(p-1).*sign(t(j));
   grad = g;
end
end