Main Content

パレート フロントの生成とプロット

ライブ スクリプトを開く

この例では、fgoalattain を使用して 2 次元多目的関数のパレート フロントを生成し、プロットする方法を説明します。

この例の 2 つの目的関数は、凸関数 1+x2 をシフトしてスケーリングしたバージョンです。目的関数のコードは、この例の最後に記載された simple_mult 補助関数内に表示されます。

両方の目的関数が、領域 x≤0 で減少し、領域 x≥1 で増加します。0 と 1 の間では、f1(x) が増加し、f2(x) が減少するため、トレードオフ領域が存在します。x から -1/2 までの範囲の 3/2 の 2 つの目的関数をプロットします。

t = linspace(-1/2,3/2);
F = simple_mult(t);
plot(t,F,'LineWidth',2)
hold on
plot([0,0],[0,8],'g--');
plot([1,1],[0,8],'g--');
plot([0,1],[1,6],'k.','MarkerSize',15);
text(-0.25,1.5,'Minimum(f_1(x))')
text(.75,5.5,'Minimum(f_2(x))')
hold off
legend('f_1(x)','f_2(x)')
xlabel({'x';'Tradeoff region between the green lines'})

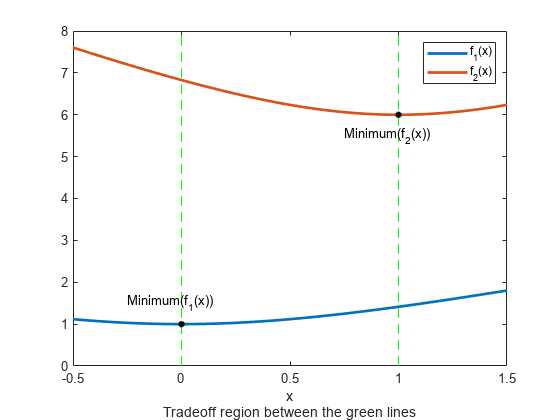
パレート フロントを見つけるには、まず、2 つの目的関数の制約なしの最小値を求めます。この例では、プロットから、f1(x) の最小値が 1 で、f2(x) の最小値が 6 であることがわかりますが、通常は最適化ルーチンを使用して最小値を求める必要があります。

その場合、多目的関数の特定の成分を返す関数を記述するのが一般的です。(この例の最後にある pickindex 補助関数が k 番目の目的関数値を返します)。次に、最適化ソルバーを使って各成分の最小値を求めます。ここでは fminbnd を使用できますが、より高次元の問題では fminunc を使用します。

k = 1;
[min1,minfn1] = fminbnd(@(x)pickindex(x,k),-1,2);
k = 2;
[min2,minfn2] = fminbnd(@(x)pickindex(x,k),-1,2);

各目的関数の制約なしの最適解をゴールに設定します。目的関数が互いに干渉しない、つまり、トレードオフが存在しない場合にのみ、これらのゴールを同時に達成できます。

goal = [minfn1,minfn2];

パレート フロントを計算するには、a が 0 から 1 の重みベクトル [a,1–a] を使用します。この重みをさまざまな値に設定して、ゴール到達問題を解きます。

nf = 2; % Number of objective functions
N = 50; % Number of points for plotting
onen = 1/N;
x = zeros(N+1,1);
f = zeros(N+1,nf);
fun = @simple_mult;
x0 = 0.5;
options = optimoptions('fgoalattain','Display','off');
for r = 0:N
t = onen*r; % 0 through 1
weight = [t,1-t];
[x(r+1,:),f(r+1,:)] = fgoalattain(fun,x0,goal,weight,...
[],[],[],[],[],[],[],options);
end
figure
plot(f(:,1),f(:,2),'ko');
xlabel('f_1')
ylabel('f_2')

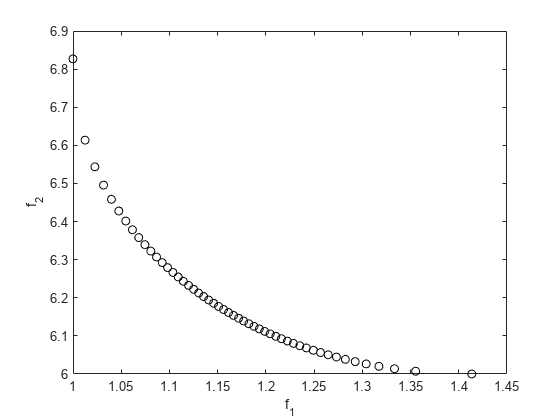
2 つの目的関数間のトレードオフを確認できます。

補助関数

次のコードは関数 simple_multi を作成します。

function f = simple_mult(x)
f(:,1) = sqrt(1+x.^2);
f(:,2) = 4 + 2*sqrt(1+(x-1).^2);
end

次のコードは関数 pickindex を作成します。

function z = pickindex(x,k)
z = simple_mult(x); % evaluate both objectives
z = z(k); % return objective k
end

参考

関連するトピック