このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

方向、位置、および座標の規則

Navigation Toolbox™ を使用して、プラットフォームの方向、位置、姿勢、および軌跡を追跡できます。"プラットフォーム" とは一般に、その状態を追跡する任意のオブジェクトを指します。

方向

"方向" は角変位によって定義されます。方向は、点または座標系の回転の観点から説明できます。点の回転では、座標系は静的であり、点が移動します。座標系の回転では、点は静的であり、座標系が移動します。特定の回転軸と回転角度に対して、点の回転と座標系の回転は同等の角変位を定義しますが、方向は逆です。

Navigation Toolbox の既定は座標系の回転です。

座標系の表現では、方向は、親座標系を子座標系に移動する回転として定義されます。親座標系と子座標系の選択は、解く問題によって異なります。たとえば、プラットフォームへのセンサーの取り付けを操作する場合、プラットフォームのボディ座標系を親座標系として選択し、センサー取り付けの座標系を子座標系として選択できます。プラットフォームのボディ座標系からセンサー取り付けの座標系までの回転により、プラットフォームを基準としたセンサーの方向が定義されます。

Navigation Toolbox は主に NED (北-東-下) 座標系をサポートしています。多くの機能で ENU (東-北-上) 座標系を使用することもできます。

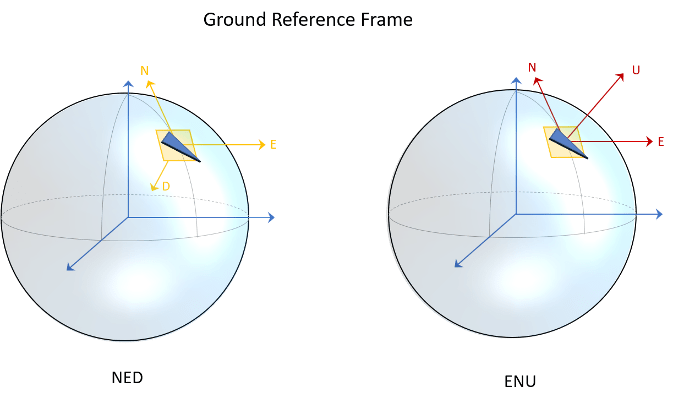
座標系の回転

ある方向を別の方向に関連付けるには、座標系を回転する必要があります。次の表は、z-y-x 回転規則をまとめたものです。z-x-z 回転規則など、他の規則を使用することもできます。これらの規則の詳細については、quaternion の回転シーケンス (RS) 引数を参照してください。

変数	オイラー角	記号	出力区間 (度)
z	ヨー	ψ	−180 ≤ ψ < 180
y	ピッチ	θ	−90 ≤ θ ≤ 90
x	ロール	ϕ	−180 ≤ ϕ < 180

正の回転角度は、原点から軸の正の方向を見たときの、軸を中心とした時計回りの回転に対応します。これは右手系と同等であり、正回転は、親指が回転軸の方向を向いているときに右手の指が曲がる方向によって示されます。

3 次元座標系の回転を定義するには、軸を中心に順番に回転する必要があります。Navigation Toolbox は、内因性 (回転後の座標系を基準とする) 回転を使用します。内因性回転では、各回転の後、次の回転の前に軸が更新されます。たとえば、z-y-x 規則を使用して軸を回転するには、次のようにします。

1. z 軸を中心として親座標系を回転して、新しい軸セット (x',y',z) を得ます。ここで、x 軸と y 軸は x' 軸と y' 軸に変更されており、z 軸は変更されていません。

   $$\left[\begin{array}{c}{x}^{\text{'}}\\ y^{\text{'}}\\ z\end{array}\right]={\text{R}}_z\left(\psi \right)\left[\begin{array}{c}x\\ y\\ z\end{array}\right]$$

2. y' 軸を中心として新しい軸セットを回転して、別の新しい軸セット (x'',y',z') を得ます。

   $$\left[\begin{array}{c}{x}^{\text{'}\text{'}}\\ y^{\text{'}}\\ z^{\text{'}}\end{array}\right]={\text{R}}_y\left(\theta \right)\left[\begin{array}{c}{x}^{\text{'}}\\ y^{\text{'}}\\ z\end{array}\right]$$

3. x'' 軸を中心としてこの新しい軸セットを回転し、目的の子座標系 (x'',y'',z'') に到達します。

   $$\left[\begin{array}{c}{x}^{\text{'}\text{'}}\\ y^{\text{'}\text{'}}\\ z^{\text{'}\text{'}}\end{array}\right]={\text{R}}_x\left(\varphi \right)\left[\begin{array}{c}{x}^{\text{'}\text{'}}\\ y^{\text{'}}\\ z^{\text{'}}\end{array}\right]$$

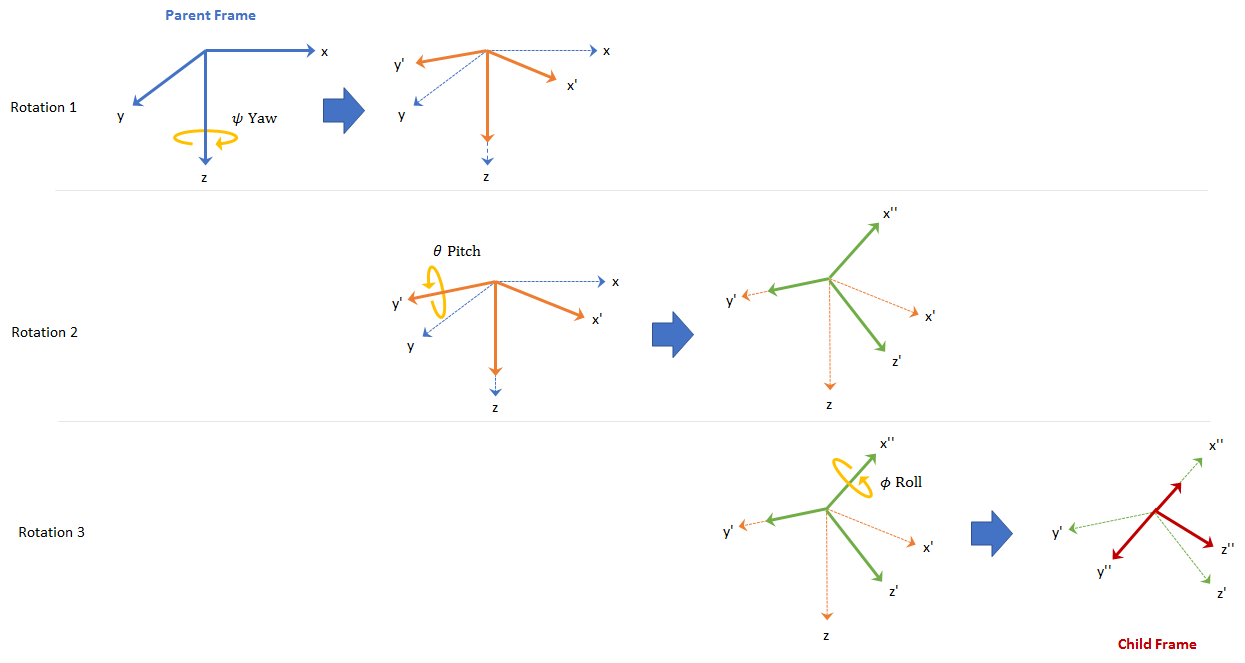
この回転シーケンスは、Rotations, Orientation, and Quaternionsで概説している規則に従っています。特定のヨー、ピッチ、およびロールについて、親座標系のベクトルを子座標系のベクトルに変換するために必要な回転行列は、次のように計算されます。

$$\text{R}\left(\psi ,\theta ,\varphi \right)={\text{R}}_x\left(\varphi \right){\text{R}}_y\left(\theta \right){\text{R}}_z\left(\psi \right)=\left[\begin{array}{ccc}\cos \psi \cos \theta & \sin \psi \cos \theta & -\sin \theta \\ \cos \psi \sin \theta \sin \varphi -\sin \psi \cos \varphi & \sin \psi \sin \theta \sin \varphi +\cos \psi \cos \varphi & \cos \theta \sin \varphi \\ \cos \psi \sin \theta \cos \varphi +\sin \psi \sin \varphi & \sin \psi \sin \theta \cos \varphi -\cos \psi \sin \varphi & \cos \theta \cos \varphi \end{array}\right]$$

座標系ベースの処理をサポートしている機能の場合、Navigation Toolbox は N 行 3 列の行列として座標を提供します。ここで、N は時間内のサンプル数で、3 つの列は x 軸、y 軸、および z 軸に対応しています。次の計算により、親座標系を子座標系に回転します。

$$a_{\text{child}}={\left(\text{R}\left(\psi ,\theta ,\varphi \right)\times {\left(a_{\text{parent}}\right)}^{\text{T}}\right)}^{\text{T}}$$

ここで、a_parent は、親座標系で表現された座標の N 行 3 列の行列を表し、a_child は、結果として得られた、子座標系で表現された座標の N 行 3 列の行列です。

Navigation Toolbox では、quaternion データ型を使用して効率的に方向を計算できます。四元数を使用して回転行列を作成するには、rotmat 関数を使用します。

ボディ座標系における重力ベクトルの表現

NED 座標系では、重力ベクトルは次のように表現できます。

gNED = [0 0 9.8]; % m/s^2

親 NED 座標系からヨー方向に 20 度、ピッチ方向に 5 度、ロール方向に 10 度の連続回転を行って得られるボディ座標系を考えます。

yaw = 20; % degree
pitch = 5; % degree
roll = 10; % degree

ボディ座標系における重力ベクトルの表現を得るには、まず、連続する 3 つのオイラー角に対応する quaternion を取得します。

q = quaternion([yaw pitch roll],"eulerd","zyx","frame");

次に、rotateframe オブジェクト関数を使用して、ボディ座標系における重力ベクトルの座標を次のように得ることができます。

gBody = rotateframe(q,gNED)

gBody = 1×3

   -0.8541    1.6953    9.6144

あるいは、回転行列を使用して座標を得ることもできます。まず、quaternion の rotmat オブジェクト関数を使用して、NED 座標系からボディ座標系に座標を変換する、対応する回転行列を取得します。

R = rotmat(q,"frame");

次に、ボディ座標系における重力ベクトルの座標を次のように得ます。

gBody2 = (R*gNED')'

gBody2 = 1×3

   -0.8541    1.6953    9.6144

位置

"位置" は、親座標系の原点から子座標系の原点までの並進距離として定義されます。たとえば、ローカル NED 座標系を親座標系とします。NED 座標系で、以下のようになります。

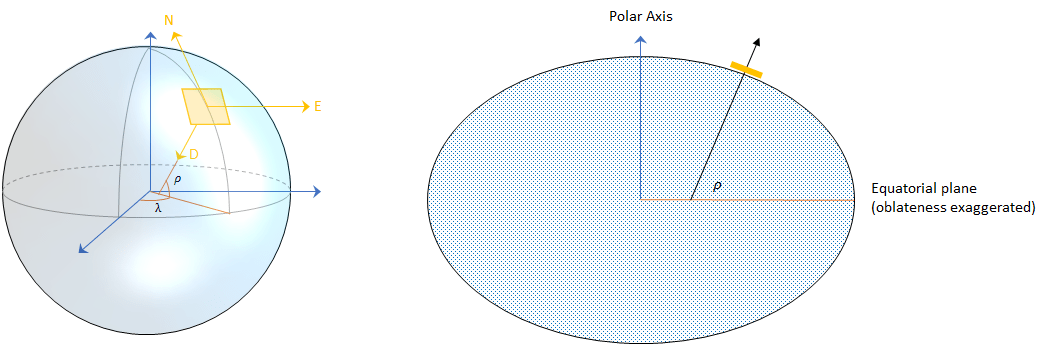
• 原点は、地球の表面上の 1 点に任意に固定されます。これにより、NED 座標系が "ローカル" になります。

• x 軸は楕円体の北を指します。

• y 軸は楕円体の東を指します。

• z 軸は、楕円体の法線方向に沿って下を指します (測地緯度 ρ)。

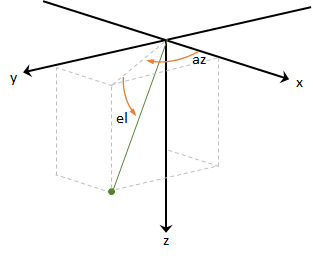
方位角と仰角

R³ のベクトルが与えられたものとします。

• "方位角" は、x 軸から、xy 平面へのベクトルの直交投影までの角度として定義されます。角度は x 軸から y 軸に向かう方向が正です。方位角は [-180, 180) の範囲の度で示されます。

• "仰角" は、xy 平面への投影からベクトルまでの角度として定義されます。角度は、xy 平面から z 軸に向かう方向が正です。仰角は [-90, 90] の範囲の度で示されます。

姿勢と軌跡

3 次元空間内のオブジェクトを完全に指定するには、位置と方向を組み合わせます。"姿勢" は、位置と方向の組み合わせとして定義されます。"軌跡" は、経時的な姿勢の変化を定義します。Navigation Toolbox でグラウンド トゥルース軌跡を生成するには、kinematicTrajectory または waypointTrajectory を使用します。

参考

quaternion | transformMotion | Rotations, Orientation, and Quaternions

参照

[1] IEEE. Standard for Distributed Interactive Simulation – Application Protocols. IEEE P1278.1/D16, Rev 18, May 2012.