磁力計キャリブレーション
磁力計は、センサーの X、Y、および Z 軸に沿って磁場の強さを検出します。正確な磁場測定は、センサー フュージョンと機首方位と方向の判別に不可欠です。
機首方位と方向の計算に役立つように、一般的な低コストの MEMS 磁力計をキャリブレーションして、環境ノイズや製造上の欠陥を補正する必要があります。
理想的な磁力計
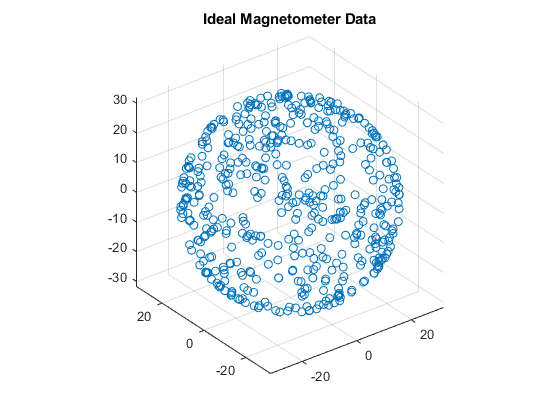
理想的な 3 軸磁力計は、直交する X、Y、および Z 軸に沿って磁場の強さを測定します。磁気干渉がなければ、磁力計の測定値は地球の磁場を測定します。センサーをすべての可能な方向に回転させながら磁力計の測定を行った場合、測定値は球上にあります。球の半径が磁場の強さになります。
磁場サンプルを生成するには、imuSensor オブジェクトを使用します。これらの目的のために、各方向で角速度と加速度がゼロであると仮定するのが安全です。
N = 500; rng(1); acc = zeros(N,3); av = zeros(N,3); q = randrot(N,1); % uniformly distributed random rotations imu = imuSensor('accel-mag'); [~,x] = imu(acc,av,q); scatter3(x(:,1),x(:,2),x(:,3)); axis equal title('Ideal Magnetometer Data');
硬鉄の影響
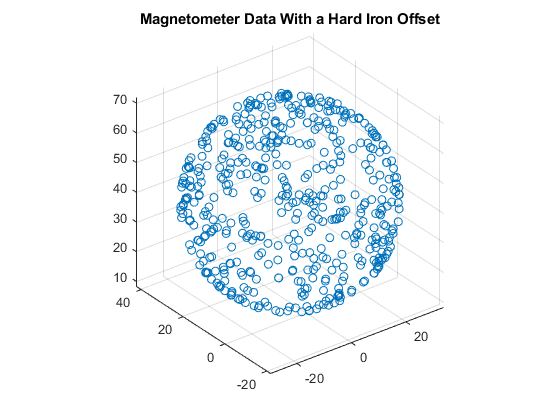
ノイズ源や製造上の欠陥により、磁力計の測定値が劣化します。これらの中で最も顕著なのは、硬鉄の影響です。硬鉄の影響は、固定的な干渉磁気ノイズ源です。多くの場合、磁力計を備えた回路基板上の他の金属物体から発生します。硬鉄の影響により、理想的な球体の原点が変わります。
imu.Magnetometer.ConstantBias = [2 10 40]; [~,x] = imu(acc,av,q); figure; scatter3(x(:,1),x(:,2),x(:,3)); axis equal title('Magnetometer Data With a Hard Iron Offset');
軟鉄の影響
軟鉄の影響は軽微です。これは、周囲の磁場を歪めるセンサー近くの物体から発生します。理想的な測定値の球を引き伸ばしたり傾けたりする効果があります。結果として得られる測定値は楕円体上にあります。
軟鉄磁場の影響は、IMU の地磁気ベクトルをセンサーの座標軸に従って回転させて引き伸ばしてから、グローバル座標系に従って再び回転することによってシミュレーションできます。
nedmf = imu.MagneticField; Rsoft = [2.5 0.3 0.5; 0.3 2 .2; 0.5 0.2 3]; soft = rotateframe(conj(q),rotateframe(q,nedmf)*Rsoft); for ii=1:numel(q) imu.MagneticField = soft(ii,:); [~,x(ii,:)] = imu(acc(ii,:),av(ii,:),q(ii)); end figure; scatter3(x(:,1),x(:,2),x(:,3)); axis equal title('Magnetometer Data With Hard and Soft Iron Effects');

補正手法
magcal 関数を使用して、硬鉄と軟鉄の両方の影響を考慮した磁力計のキャリブレーション パラメーターを決定できます。キャリブレーションされていない磁力計データは、次の方程式を使用して楕円体上にあるものとしてモデル化できます。

この方程式で、"R" は 3 行 3 列の行列、"b" は楕円体の中心を定義する 1 行 3 列のベクトル、"x" はキャリブレーションされていない磁力計測定値の 1 行 3 列のベクトル、 は磁場の強さを示すスカラーです。上の方程式は円錐曲線の一般的な形式です。楕円体の場合、"R" は正定値でなければなりません。
は磁場の強さを示すスカラーです。上の方程式は円錐曲線の一般的な形式です。楕円体の場合、"R" は正定値でなければなりません。magcal 関数は、"R" に関するさまざまな仮定に基づいて、さまざまなソルバーを使用します。magcal 関数では、"R" は単位行列、対角行列、または対称行列であると仮定できます。
magcal 関数は、オフセットの楕円体上にある測定値を取得し、原点を中心とする理想的な球面上にあるように変換する補正係数を生成します。magcal 関数は、3 行 3 列の実数行列 "A" と 1 行 3 列のベクトル "b" を返します。キャリブレーションされていないデータを補正するには、以下を計算します。

ここで、"x" はキャリブレーションされていない磁力計測定値の 1 行 3 列の配列であり、"m" は球上にある補正された磁力計測定値の 1 行 3 列の配列です。行列 "A" の行列式は 1 で、"R" の行列の平方根です。さらに、"A" は "R" と同じ形式、つまり単位行列、対角行列、または対称行列です。これらの種類の行列は回転を与えることができないため、行列 "A" は補正中に磁力計データを回転させません。
magcal 関数は、磁場の強さ  である 3 番目の出力も返します。磁場の強さを使用して、
である 3 番目の出力も返します。磁場の強さを使用して、ahrsfilter の ExpectedMagneticFieldStrength プロパティを設定できます。
magcal 関数の使用
magcal 関数を使用して、ノイズのある磁力計データを補正するキャリブレーション パラメーターを決定します。imuSensor で Magnetometer プロパティの NoiseDensity プロパティを設定して、ノイズのある磁力計データを作成します。変数 soft で回転され引き伸ばされた磁場を使用して、軟鉄の影響をシミュレーションします。
imu.Magnetometer.NoiseDensity = 0.08; for ii=1:numel(q) imu.MagneticField = soft(ii,:); [~,x(ii,:)] = imu(acc(ii,:),av(ii,:),q(ii)); end
キャリブレーションされていない磁力計データを最も適切に補正する A および b パラメーターを見つけるには、次のように関数を呼び出すだけです。
[A,b,expMFS] = magcal(x); xCorrected = (x-b)*A;
元のデータと補正されたデータをプロットします。元のデータに最もよく当てはまる楕円体を表示します。補正されたデータが配置される球を表示します。
de = HelperDrawEllipsoid;
de.plotCalibrated(A,b,expMFS,x,xCorrected,'Auto');

magcal 関数は、残留誤差を最小限に抑えるためにさまざまなソルバーを使用します。残留誤差は、キャリブレーション データと半径 expMFS の球との間の距離の合計です。
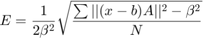
r = sum(xCorrected.^2,2) - expMFS.^2;
E = sqrt(r.'*r./N)./(2*expMFS.^2);
fprintf('Residual error in corrected data : %.2f\n\n',E);
Residual error in corrected data : 0.01
一部の欠陥のみを補正する必要がある場合、またはより単純な補正計算を実行する場合は、個別のソルバーを実行できます。
オフセットのみの計算
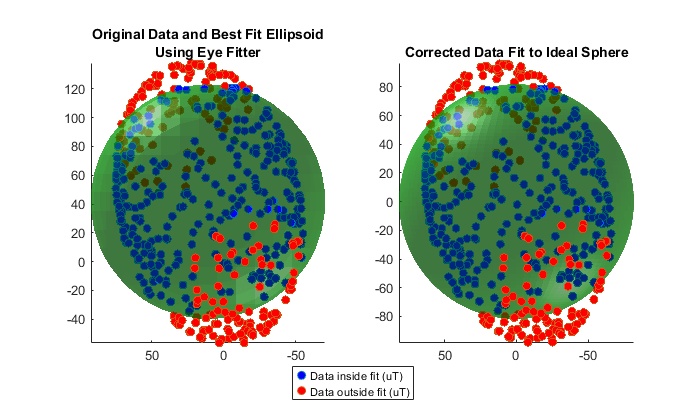
多くの MEMS 磁力計は、センサー内に硬鉄オフセットを補正するために使用できるレジスタを備えています。実際、上記の方程式の (x-b) 部分はセンサー上で発生します。硬鉄オフセット補正のみが必要な場合、A 行列は事実上単位行列になります。硬鉄補正のみを決定するには、magcal 関数を次のように呼び出すことができます。
[Aeye,beye,expMFSeye] = magcal(x,'eye'); xEyeCorrected = (x-beye)*Aeye; [ax1,ax2] = de.plotCalibrated(Aeye,beye,expMFSeye,x,xEyeCorrected,'Eye'); view(ax1,[-1 0 0]); view(ax2,[-1 0 0]);
硬鉄の補正と軸スケーリング計算
多くのアプリケーションでは、楕円体行列を対角行列として扱うだけで十分です。幾何学的には、これは、キャリブレーションされていない磁力計データの楕円体が、その半軸が座標系の軸と整列し、中心が原点からオフセットされているように近似されることを意味します。これは楕円体の実際の特性である可能性は低いですが、補正方程式が軸ごとに 1 回の乗算と 1 回の減算に減ります。
[Adiag,bdiag,expMFSdiag] = magcal(x,'diag'); xDiagCorrected = (x-bdiag)*Adiag; [ax1,ax2] = de.plotCalibrated(Adiag,bdiag,expMFSdiag,x,xDiagCorrected,... 'Diag');

硬鉄および軟鉄の完全な補正
magcal 関数に任意の楕円体を解かせて、高密度の対称 A 行列を生成するには、関数を次のように呼び出します。
[A,b] = magcal(x,'sym');
自動近似
'eye'、'diag'、および 'sym' フラグを慎重に使用し、出力値を検査する必要があります。場合によっては、高次 ('diag' または 'sym') 近似に必要なデータが不十分な場合があり、より単純な A 行列を使用してより適切な補正パラメーターのセットを見つけることができます。既定の 'auto' 近似オプションはこの状況に対応できます。
高次フィッターで使用されるデータが不十分な場合を考えてみましょう。
xidx = x(:,3) > 100;
xpoor = x(xidx,:);
[Apoor,bpoor,mfspoor] = magcal(xpoor,'diag');
'diag' オプションを使用して良好な近似と適切なキャリブレーション パラメーターを実現するには、楕円体の表面全体に広がるデータが十分ではありません。その結果、Apoor 行列は複雑になります。
disp(Apoor)
0.0000 + 0.4722i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.5981i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 3.5407 + 0.0000i
'auto' 近似オプションを使用すると、この問題が回避され、実数、対称、正定であるより単純な A 行列が見つかります。'auto' オプション文字列を指定して magcal を呼び出すことは、オプション文字列を指定せずに呼び出すことと同じです。
[Abest,bbest,mfsbest] = magcal(xpoor,'auto');
disp(Abest)
1 0 0
0 1 0
0 0 1
'auto' フィッターを使用した結果と不適切な高次フィッターを使用した結果を比較すると、データを補正する前に返された A 行列を検査しないことの危険性がわかります。
de.compareBest(Abest,bbest,mfsbest,Apoor,bpoor,mfspoor,xpoor);

既定の 'auto' フラグを指定して magcal 関数を呼び出すと、'eye'、'diag'、'sym' のすべての可能性が試行され、残留誤差を最小限に抑え、A を実数に保ち、"R" が正定値で対称であることを保証する A と b が検索されます。
まとめ
magcal 関数では、磁力計の硬鉄と軟鉄のオフセットを補正するためのキャリブレーション パラメーターを指定できます。オプション文字列を指定せずに ('auto' オプション文字列を指定するのと同等です) 関数を呼び出すと、最適な近似が得られ、ほとんどのケースに対応できます。