nlmpcmove
Compute optimal control action for nonlinear MPC controller
Syntax
Description
Nonlinear MPC
Multistage Nonlinear MPC
mv = nlmpcmove(msobj,x,lastmv,simdata)simdata structure, which contains measured
disturbances, run-time bounds, parameters for the state and stage functions, and initial
guesses for state and manipulated variable trajectories. In general use the following
syntax to return a new simdata (containing updated initial guesses)
as a second output argument.
Examples
Create a nonlinear MPC controller with six states, six outputs, and four inputs.
nx = 6; ny = 6; nu = 4; nlobj = nlmpc(nx,ny,nu);
Zero weights are applied to one or more OVs because there are fewer MVs than OVs.
Specify the controller sample time and horizons.
Ts = 0.4; p = 30; c = 4; nlobj.Ts = Ts; nlobj.PredictionHorizon = p; nlobj.ControlHorizon = c;
Specify the prediction model state function and the Jacobian of the state function. For this example, use a model of a flying robot.
nlobj.Model.StateFcn = "FlyingRobotStateFcn"; nlobj.Jacobian.StateFcn = "FlyingRobotStateJacobianFcn";
Specify a custom cost function for the controller that replaces the standard cost function.
nlobj.Optimization.CustomCostFcn = @(X,U,e,data) Ts*sum(sum(U(1:p,:))); nlobj.Optimization.ReplaceStandardCost = true;
Specify a custom constraint function for the controller.
nlobj.Optimization.CustomEqConFcn = @(X,U,data) X(end,:)';
Specify linear constraints on the manipulated variables.
for ct = 1:nu nlobj.MV(ct).Min = 0; nlobj.MV(ct).Max = 1; end
Validate the prediction model and custom functions at the initial states (x0) and initial inputs (u0) of the robot.
x0 = [-10;-10;pi/2;0;0;0]; u0 = zeros(nu,1); validateFcns(nlobj,x0,u0);
Model.StateFcn is OK. Jacobian.StateFcn is OK. No output function specified. Assuming "y = x" in the prediction model. Optimization.CustomCostFcn is OK. Optimization.CustomEqConFcn is OK. Analysis of user-provided model, cost, and constraint functions complete.
Compute the optimal state and manipulated variable trajectories, which are returned in the info.
[~,~,info] = nlmpcmove(nlobj,x0,u0);
Slack variable unused or zero-weighted in your custom cost function. All constraints will be hard.
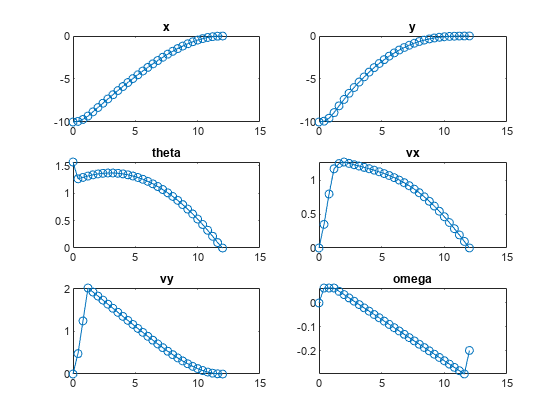
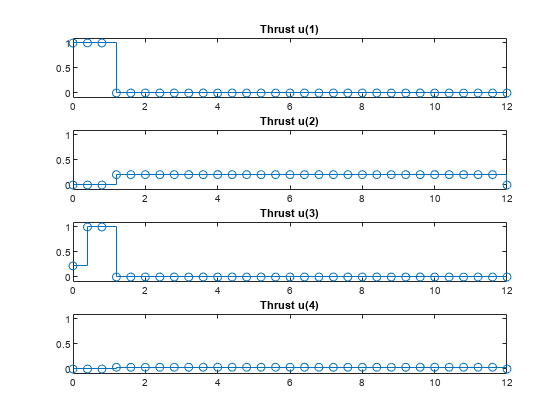
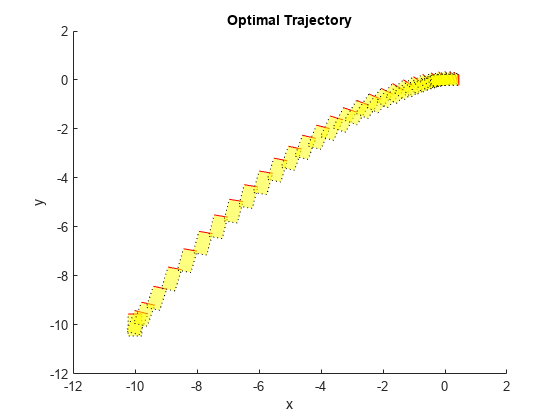
Plot the optimal trajectories.
FlyingRobotPlotPlanning(info,Ts)
Optimal fuel consumption = 1.869736
Create a nonlinear MPC controller with four states, two outputs, and one input.
nlobj = nlmpc(4,2,1);
Zero weights are applied to one or more OVs because there are fewer MVs than OVs.
Specify the sample time and horizons of the controller.
Ts = 0.1; nlobj.Ts = Ts; nlobj.PredictionHorizon = 10; nlobj.ControlHorizon = 5;
Specify the state function for the controller, which is in the file pendulumDT0.m. This discrete-time model integrates the continuous time model defined in pendulumCT0.m using a multistep forward Euler method.
nlobj.Model.StateFcn = "pendulumDT0";
nlobj.Model.IsContinuousTime = false;The prediction model uses an optional parameter, Ts, to represent the sample time. Specify the number of parameters.
nlobj.Model.NumberOfParameters = 1;
Specify the output function of the model, passing the sample time parameter as an input argument.
nlobj.Model.OutputFcn = @(x,u,Ts) [x(1); x(3)];
Define standard constraints for the controller.
nlobj.Weights.OutputVariables = [3 3]; nlobj.Weights.ManipulatedVariablesRate = 0.1; nlobj.OV(1).Min = -10; nlobj.OV(1).Max = 10; nlobj.MV.Min = -100; nlobj.MV.Max = 100;
Validate the prediction model functions.
x0 = [0.1;0.2;-pi/2;0.3];
u0 = 0.4;
validateFcns(nlobj, x0, u0, [], {Ts});Model.StateFcn is OK. Model.OutputFcn is OK. Analysis of user-provided model, cost, and constraint functions complete.
Only two of the plant states are measurable. Therefore, create an extended Kalman filter for estimating the four plant states. Its state transition function is defined in pendulumStateFcn.m and its measurement function is defined in pendulumMeasurementFcn.m.
EKF = extendedKalmanFilter(@pendulumStateFcn,@pendulumMeasurementFcn);
Define initial conditions for the simulation, initialize the extended Kalman filter state, and specify a zero initial manipulated variable value.
x = [0;0;-pi;0]; y = [x(1);x(3)]; EKF.State = x; mv = 0;
Specify the output reference value.
yref = [0 0];
Create an nlmpcmoveopt object, and specify the sample time parameter.
nloptions = nlmpcmoveopt;
nloptions.Parameters = {Ts};Run the simulation for 10 seconds. During each control interval:
Correct the previous prediction using the current measurement.
Compute optimal control moves using
nlmpcmove. This function returns the computed optimal sequences innloptions. Passing the updated options object tonlmpcmovein the next control interval provides initial guesses for the optimal sequences.Predict the model states.
Apply the first computed optimal control move to the plant, updating the plant states.
Generate sensor data with white noise.
Save the plant states.
Duration = 10; xHistory = x; for ct = 1:(Duration/Ts) % Correct previous prediction xk = correct(EKF,y); % Compute optimal control moves [mv,nloptions] = nlmpcmove(nlobj,xk,mv,yref,[],nloptions); % Predict prediction model states for the next iteration predict(EKF,[mv; Ts]); % Implement first optimal control move x = pendulumDT0(x,mv,Ts); % Generate sensor data y = x([1 3]) + randn(2,1)*0.01; % Save plant states xHistory = [xHistory x]; end
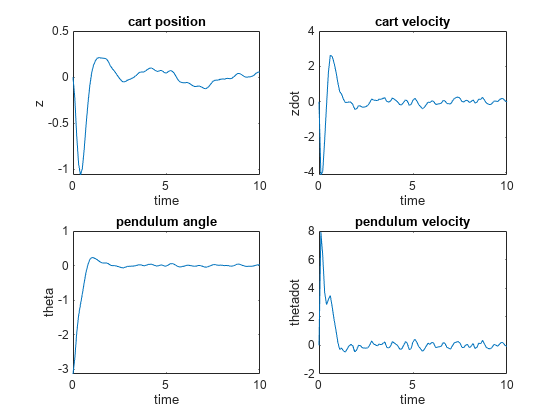
Plot the resulting state trajectories.
figure subplot(2,2,1) plot(0:Ts:Duration,xHistory(1,:)) xlabel('time') ylabel('z') title('cart position') subplot(2,2,2) plot(0:Ts:Duration,xHistory(2,:)) xlabel('time') ylabel('zdot') title('cart velocity') subplot(2,2,3) plot(0:Ts:Duration,xHistory(3,:)) xlabel('time') ylabel('theta') title('pendulum angle') subplot(2,2,4) plot(0:Ts:Duration,xHistory(4,:)) xlabel('time') ylabel('thetadot') title('pendulum velocity')
This example shows how to create and simulate a simple multistage MPC controller in closed loop, without using initial guesses, with the MATLAB® function nlmpcmove.
Create Multistage MPC Controller
Create a multistage nonlinear MPC object with a five-step horizon, one state, and one manipulated variable.
msobj = nlmpcMultistage(5,1,1);
Write a simple state function as a string.
sstr = "function xdot = mystatefcn(x,u)" + newline + ... "xdot = u-sin(x);" + newline + "end";
Write the string to the mystatefcn.m file.
sfid=fopen("mystatefcn.m","w"); fwrite(sfid,sstr,"char"); fclose(sfid);
Write a simple cost function as a string.
cstr = "function c = mycostfcn(k,x,u)" + newline + ... "c = abs(u)/k+k*x^2;" + newline + "end";
Write the string to the mycostfcn.m file.
cfid=fopen("mycostfcn.m","w"); fwrite(cfid,cstr,"char"); fclose(cfid);
Alternatively, you can write your state and cost MATLAB functions in the current folder (which is recommended because local functions are not supported for the generation of deployment code).
If files have not yet been written to the hard disk pause five second before accessing them.
if ~exist("mystatefcn","file") pause(5) end
Specify the state transition function for the prediction model.
msobj.Model.StateFcn = "mystatefcn";Specify the cost functions for last three stages.
for i=3:6 msobj.Stages(i).CostFcn = "mycostfcn"; end
Note that, because the Jacobian of the state function is not supplied here, nlmpcmove needs to numerically calculate them at each time step, which negatively affects performance. As a best practice, supply the Jacobian of the state function, as shown in Simulate Multistage Nonlinear MPC Controller Using Initial Guesses. You can also automatically generate a Jacobian function using generateJacobianFunction.
Simulate Controller in Closed Loop
Initialize the plant state and input.
x=3; mv=0;
Validate functions.
validateFcns(msobj,x,mv);
Model.StateFcn is OK. "CostFcn" of the following stages [3 4 5 6] are OK. Analysis of user-provided model, cost, and constraint functions complete.
Simulate the control loop for 5 steps, without updating the initial guess. Use the Euler method, that is dx(t)/dt ~ (x(t+1)-x(t))/Ts, to simulate the plant.
for k=1:5 % calculate move (without initial guess) mv = nlmpcmove(msobj, x, mv); % update plant state assuming Ts=0.2s x=x+0.2*mystatefcn(x,mv); end
Note that, because initial guesses are not supplied as an input argument, nlmpcmove needs to recalculate them at each time step, which negatively affects performance. Not supplying initial guesses can be an acceptable starting point, but in general is not suggested. As a best practice, use updated initial guesses at each time step, as shown in Simulate Multistage Nonlinear MPC Controller Using Initial Guesses, so that nlmpcmove does not need to recalculate them at each time step (in the same example you also use ode45 to calculate the evolution of the plant state until the next control interval).
Display the final values of the state and manipulated variables.
disp(['Final value of x =' num2str(x)])Final value of x =1.3074
disp(['Final value of mv =' num2str(mv)])Final value of mv =-0.35102
This example shows how to create and simulate a simple multistage MPC controller in closed loop using initial guesses, with the MATLAB® function nlmpcmove.
Create Multistage MPC Controller
Create a multistage MPC object with a seven-steps horizon, one state, and one manipulated variable.
msobj = nlmpcMultistage(7,1,1);
Defining your state and cost functions as separate files in the current folder on in a folder on the MATLAB path is recommended, as local functions are not supported for the generation of C/C++ deployment code. However, for this example, the state, cost, and state Jacobian functions are defined as local functions at the end of the example.
Specify the state transition function for the prediction model.
msobj.Model.StateFcn = @mystatefcn;
As a best practice, use Jacobians whenever they are available, otherwise the solver must compute it numerically. You can also automatically generate a Jacobian function using generateJacobianFunction.
Specify the Jacobian of the state transition function.
msobj.Model.StateJacFcn = @mystatejac;
Specify the cost functions for all stages except the first.
for i=2:8 msobj.Stages(i).CostFcn = @mycostfcn; end
Define Initial Conditions, Create Data Structure, and Validate Functions
Initialize the plant state and input.
x=3; mv=0;
Create the initial simulation data structure.
simdata = getSimulationData(msobj)
simdata = struct with fields:
InitialGuess: []
Validate functions and the data structure.
validateFcns(msobj,x,mv,simdata);
Model.StateFcn is OK. Model.StateJacFcn is OK. "CostFcn" of the following stages [2 3 4 5 6 7 8] are OK. Analysis of user-provided model, cost, and constraint functions complete.
Simulate Controller in Closed Loop
Simulate the control loop for 5 steps.
for k=1:5 % calculate move and update simdata [mv,simdata] = nlmpcmove(msobj, x, mv, simdata); % simulate plant for one sample time [~,xhist] = ode45(@(t,xode) mystatefcn(xode,mv),[0 msobj.Ts],x); % update plant state x = xhist(end); end
Since updated initial guesses are supplied as an input argument within the simdata structure, nlmpcmove does not need to recalculate them at each time step, which saves computation time and improves performance. Updating initial guesses at every time step is a best practice.
Display the last values of the state and manipulated variables.
disp(['Final value of x =' num2str(x)])Final value of x =-0.039868
disp(['Final value of mv =' num2str(mv)])Final value of mv =-0.067044
Support Functions
State transition function.
function xdot = mystatefcn(x,u) xdot = u-sin(x); end
Jacobian of the state transition function.
function [A,B] = mystatejac(x,~) A = -cos(x); B = 1; end
Stage cost functions.
function j = mycostfcn(s,x,u) j = abs(u)/s+s*x^2; end
Input Arguments
Nonlinear MPC controller, specified as an nlmpc
object.
Multistage nonlinear MPC controller, specified as an nlmpcMultistage
object.
Current prediction model states, specified as a vector of lengthNx, where Nx is the number of prediction model states. Since the nonlinear MPC controller does not perform state estimation, you must either measure or estimate the current prediction model states at each control interval. For more information on nonlinear MPC prediction models, see Specify Prediction Model for Nonlinear MPC.
Control signals used in plant at previous control interval, specified as a vector of lengthNmv, where Nmv is the number of manipulated variables.
Note
Specify lastmv as the manipulated variable signals applied to
the plant in the previous control interval. Typically, these signals are the values
generated by the controller, though this is not always the case. For example, if your
controller is offline and running in tracking mode; that is, the controller output is
not driving the plant, then feeding the actual control signal to
last_mv can help achieve bumpless transfer when the controller
is switched back online.
Plant output reference values, specified as a row vector of length
Ny or an array with
Ny columns, where
Ny is the number of output variables. If
you do not specify ref, the default reference values are
zero.
To use the same reference values across the prediction horizon, specify a row vector.
To vary the reference values over the prediction horizon from time k+1 to time k+p, specify an array with up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the reference values for one prediction horizon step. If you specify fewer than p rows, the values in the final row are used for the remaining steps of the prediction horizon.
Measured disturbance values, specified as a row vector of length
Nmd or an array with
Nmd columns, where
Nmd is the number of measured
disturbances. If your controller has measured disturbances, you must specify
md. If your controller has no measured disturbances, specify
md as [].
To use the same disturbance values across the prediction horizon, specify a row vector.
To vary the disturbance values over the prediction horizon from time k to time k+p, specify an array with up to p+1 rows. Here, k is the current time and p is the prediction horizon. Each row contains the disturbance values for one prediction horizon step. If you specify fewer than p rows, the values in the final row are used for the remaining steps of the prediction horizon.
Run-time options, specified as an nlmpcmoveopt
object. Using these options, you can:
Tune controller weights
Update linear constraints
Set manipulated variable targets
Specify prediction model parameters
Provide initial guesses for state and manipulated variable trajectories
These options apply to only the current nlmpcmove time
instant.
To improve solver efficiency, it is best practice to specify initial guesses for the state and manipulated variable trajectories.
Run-time simulation data, specified as structure. It must be initially created by
getSimulationData, and then populated (if needed) before being passed to
nlmpcmove as an input argument. An updated version is then always
returned as a second output argument of nlmpcmove. Note that the
MVMin, MVMax, StateMin,
StateMax, MVRateMin,
MVRateMax fields are needed only if you want to change these
bounds at run time. These fields exist in the structure returned by
getSimulationData only if you enable them explicitly when calling
getSimulationData. The simdata structure has
the following fields.
Measured disturbance values, specified as a row vector of length
Nmd or an array with
Nmd columns, where
Nmd is the number of measured
disturbances. If your multistage MPC object has any measured disturbance channel
defined, you must specify MeasuredDisturbance. If your
controller has no measured disturbances, this field does not exist in the
structure generated by getSimulationData.
To use the same disturbance values across the prediction horizon, specify a row vector.
To vary the disturbance values over the prediction horizon from time k to time k+p, specify an array with up to p+1 rows. Here, k is the current time and p is the prediction horizon. Each row contains the disturbance values for one prediction horizon step. If you specify fewer than p rows, the values in the final row are used for the remaining steps of the prediction horizon.
Manipulated variable lower bounds, specified as a row vector of length
Nmv or a matrix with
Nmv columns, where
Nmv is the number of manipulated
variables. MVMin(:,i) replaces the
ManipulatedVariables(i).Min property of the controller at run
time.
To use the same bounds across the prediction horizon, specify a row vector.
To vary the bounds over the prediction horizon from time k to time k+p-1, specify a matrix with up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the final bounds are used for the remaining steps of the prediction horizon.
Manipulated variable upper bounds, specified as a row vector of length
Nmv or a matrix with
Nmv columns, where
Nmv is the number of manipulated
variables. MVMax(:,i) replaces the
ManipulatedVariables(i).Max property of the controller at run
time.
To use the same bounds across the prediction horizon, specify a row vector.
To vary the bounds over the prediction horizon from time k to time k+p-1, specify a matrix with up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the final bounds are used for the remaining steps of the prediction horizon.
Manipulated variable rate lower bounds, specified as a row vector of length
Nmv or a matrix with
Nmv columns, where
Nmv is the number of manipulated
variables. MVRateMin(:,i) replaces the
ManipulatedVariables(i).RateMin property of the controller at
run time. MVRateMin bounds must be nonpositive.
To use the same bounds across the prediction horizon, specify a row vector.
To vary the bounds over the prediction horizon from time k to time k+p-1, specify a matrix with up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the final bounds are used for the remaining steps of the prediction horizon.
Manipulated variable rate upper bounds, specified as a row vector of length
Nmv or a matrix with
Nmv columns, where
Nmv is the number of manipulated
variables. MVRateMax(:,i) replaces the
ManipulatedVariables(i).RateMax property of the controller at
run time. MVRateMax bounds must be nonnegative.
To use the same bounds across the prediction horizon, specify a row vector.
To vary the bounds over the prediction horizon from time k to time k+p-1, specify a matrix with up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the final bounds are used for the remaining steps of the prediction horizon.
State lower bounds, specified as a row vector of length
Nx or a matrix with
Nx columns, where
Nx is the number of states.
StateMin(:,i) replaces the States(i).Min
property of the controller at run time.
To use the same bounds across the prediction horizon, specify a row vector.
To vary the bounds over the prediction horizon from time k+1 to time k+p, specify a matrix with up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the final bounds are used for the remaining steps of the prediction horizon.
State upper bounds, specified as a row vector of length
Nx or a matrix with
Nx columns, where
Nx is the number of states.
StateMax(:,i) replaces the States(i).Max
property of the controller at run time.
To use the same bounds across the prediction horizon, specify a row vector.
To vary the bounds over the prediction horizon from time k+1 to time k+p, specify a matrix with up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the final bounds are used for the remaining steps of the prediction horizon.
State function parameter values, specified as a vector with length equal to
the value of the Model.ParameterLength property of the
multistage controller object. If Model.StateFcn needs a
parameter vector, you must provide its value at runtime using this field. If
Model.ParameterLength is 0 this field does
not exist in the structure returned by
getSimulationData.
Stage functions parameter values, specified as a vector with length equal to
the sum of all the values in the Stages(i).ParameterLength
properties of the multistage controller object. If any cost or constraint function
defined in the Stages property needs a parameter vector, you
must provide all the parameter vectors at runtime (stacked in a single column)
using this field. If none of your stage functions have parameters, this field does
not exist in the structure returned by
getSimulationData.
You must stack the parameter vectors for all stages in the column vector
StateFcnParameters as
follows.
[parameter vector for stage 1; parameter vector for stage 2; ... parameter vector for stage p+1; ]
Terminal state, specified as a column vector with as many elements as the
number of states. The terminal state is the desired state at the last prediction
step. To specify desired terminal states at run-time via this field, you must
specify finite values in the TerminalState field of the
Model property of msobj. Specify
inf for the states that do not need to be constrained to a
terminal value. At run time, nlmpcmove ignores any values in the
TerminalState field of simdata that
correspond to inf values in msobj. If you
do not specify any terminal value condition in msobj, this
field is not created in simdata.
If there is no TerminalState in
simdata then the terminal state constraint (if present)
does not change at run time.
Initial guesses for the decision variables, specified as a column vector of
length equal to the sum of the lengths of all the decision variable vectors for
each stage. Good initial guesses are important since they help the solver to
converge to a solution faster. Therefore, when simulating a control loop by
calling nlmpcmove repeatedly in a loop, pass
simdata as an input argument (so initial guesses can be
used), and at the same time return an updated version of
simdata (with new initial guesses for the next control
interval) as an output argument.
You must be stack the initial guesses for all stages in the column vector
InitialGuess as
follows.
[state vector guess for stage 1; manipulated variable vector guess for stage 1; manipulated variable vector rate guess for stage 1; % if used slack variable vector guess for stage 1; % if used state vector guess for stage 2; manipulated variable vector guess for stage 2; manipulated variable vector rate guess for stage 2; % if used slack variable vector guess for stage 2; % if used ... state vector guess for stage p; manipulated variable vector guess for stage p; manipulated variable vector rate guess for stage p; % if used slack variable vector guess for stage p; % if used state vector guess for stage p+1; slack variable vector guess for stage p+1; % if used ]
If InitialGuess is [], the default
initial guesses are calculated from the x and
lastmv arguments passed to
nlmpcmove.
In general, during closed-loop simulation, you do not specify
InitialGuess yourself. Instead, when calling nlmpcmove, return the simdata output argument,
which contains the calculated initial guesses for the next control interval. You
can then pass simdata as an input argument to
nlmpcmove for the next control interval. These steps are a
best practice, even if you do not specify any other run-time options.
Output Arguments
Optimal manipulated variable control action, returned as a column vector of length Nmv, where Nmv is the number of manipulated variables.
If the solver converges to a local optimum solution
(info.ExitFlag is positive), then mv contains
the optimal solution.
If the solver reaches the maximum number of iterations without finding an optimal
solution (info.ExitFlag = 0) and:
nlobj.Optimization.UseSuboptimalSolutionistrue, thenmvcontains the suboptimal solutionnlobj.Optimization.UseSuboptimalSolutionisfalse, thenmvcontainslastmv
If the solver fails (info.ExitFlag is negative), then
mv contains lastmv.
Run-time options with initial guesses for the state and manipulated variable
trajectories to be used in the next control interval, returned as an nlmpcmoveopt
object. Any run-time options that you specified using options, such
as weights, constraints, or parameters, are copied to opt.
The initial guesses for the states (opt.X0) and manipulated
variables (opt.MV0) are the optimal trajectories computed by
nlmpcmove and correspond to the last p-1 rows
of info.Xopt and info.MVopt, respectively.
To use these initial guesses in the next control interval, specify
opt as the options input argument to
nlmpcmove.
Solution details, returned as a structure with the following fields.
Optimal manipulated variable sequence, returned as a (p+1)-by-Nmv array, where p is the prediction horizon and Nmv is the number of manipulated variables.
MVopt(i,:) contains the calculated optimal manipulated
variable values at time k+i-1, for i =
1,...,p, where k is the current time.
MVopt(1,:) contains the same manipulated variable values as
output argument mv. Since the controller does not calculate
optimal control moves at time k+p,
MVopt(p+1,:) is equal to
MVopt(p,:).
Optimal prediction model state sequence, returned as a (p+1)-by-Nx array, where p is the prediction horizon and Nx is the number of states in the prediction model.
Xopt(i,:) contains the calculated state values at time
k+i-1, for i = 2,...,p+1, where
k is the current time. Xopt(1,:) is the
same as the current states in x.
Optimal output variable sequence, returned as a (p+1)-by-Ny array, where p is the prediction horizon and Ny is the number of outputs.
Yopt(i,:) contains the calculated output values at time
k+i-1, for i = 2,...,p+1, where
k is the current time. Yopt(1,:) is
computed based on the current states in x and the current
measured disturbances in md, if any.
Prediction horizon time sequence, returned as a column vector of length
p+1, where p is the prediction horizon.
Topt contains the time sequence from time
k to time k+p, where
k is the current time.
Topt(1) = 0 represents the current time. Subsequent time
steps Topt(i) are Ts*(i-1), where
Ts is the controller sample time.
Use Topt when plotting the MVopt,
Xopt, or Yopt sequences.
Stacked slack variables vector, used in constraint softening. If all elements are zero, then all soft constraints are satisfied over the entire prediction horizon. If any element is greater than zero, then at least one soft constraint is violated.
The slack variable vector for all stages are stacked as:
[slack variable vector for stage 1; % if used slack variable vector for stage 2; % if used ... slack variable vector for stage p+1; % if used ]
Optimization exit code, returned as one of the following:
Positive Integer — Optimal solution found
0— Feasible suboptimal solution found after the maximum number of iterationsNegative integer — No feasible solution found
Number of iterations used by the nonlinear programming solver, returned as a positive integer.
Objective function cost, returned as a nonnegative scalar value. The cost quantifies the degree to which the controller has achieved its objectives.
The cost value is only meaningful when ExitFlag is
nonnegative.
Updated run-time simulation data, returned as a structure, containing new initial guesses for the state and manipulated trajectories to be used in the next control interval. It is a structure with the following fields.
Measured disturbance values, specified as a row vector of length
Nmd or an array with
Nmd columns, where
Nmd is the number of measured
disturbances. If your multistage MPC object has any measured disturbance channel
defined, you must specify MeasuredDisturbance. If your
controller has no measured disturbances, this field does not exist in the
structure generated by getSimulationData.
To use the same disturbance values across the prediction horizon, specify a row vector.
To vary the disturbance values over the prediction horizon from time k to time k+p, specify an array with up to p+1 rows. Here, k is the current time and p is the prediction horizon. Each row contains the disturbance values for one prediction horizon step. If you specify fewer than p rows, the values in the final row are used for the remaining steps of the prediction horizon.
Manipulated variable lower bounds, specified as a row vector of length
Nmv or a matrix with
Nmv columns, where
Nmv is the number of manipulated
variables. MVMin(:,i) replaces the
ManipulatedVariables(i).Min property of the controller at run
time.
To use the same bounds across the prediction horizon, specify a row vector.
To vary the bounds over the prediction horizon from time k to time k+p-1, specify a matrix with up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the final bounds are used for the remaining steps of the prediction horizon.
Manipulated variable upper bounds, specified as a row vector of length
Nmv or a matrix with
Nmv columns, where
Nmv is the number of manipulated
variables. MVMax(:,i) replaces the
ManipulatedVariables(i).Max property of the controller at run
time.
To use the same bounds across the prediction horizon, specify a row vector.
To vary the bounds over the prediction horizon from time k to time k+p-1, specify a matrix with up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the final bounds are used for the remaining steps of the prediction horizon.
Manipulated variable rate lower bounds, specified as a row vector of length
Nmv or a matrix with
Nmv columns, where
Nmv is the number of manipulated
variables. MVRateMin(:,i) replaces the
ManipulatedVariables(i).RateMin property of the controller at
run time. MVRateMin bounds must be nonpositive.
To use the same bounds across the prediction horizon, specify a row vector.
To vary the bounds over the prediction horizon from time k to time k+p-1, specify a matrix with up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the final bounds are used for the remaining steps of the prediction horizon.
Manipulated variable rate upper bounds, specified as a row vector of length
Nmv or a matrix with
Nmv columns, where
Nmv is the number of manipulated
variables. MVRateMax(:,i) replaces the
ManipulatedVariables(i).RateMax property of the controller at
run time. MVRateMax bounds must be nonnegative.
To use the same bounds across the prediction horizon, specify a row vector.
To vary the bounds over the prediction horizon from time k to time k+p-1, specify a matrix with up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the final bounds are used for the remaining steps of the prediction horizon.
State lower bounds, specified as a row vector of length
Nx or a matrix with
Nx columns, where
Nx is the number of states.
StateMin(:,i) replaces the States(i).Min
property of the controller at run time.
To use the same bounds across the prediction horizon, specify a row vector.
To vary the bounds over the prediction horizon from time k+1 to time k+p, specify a matrix with up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the final bounds are used for the remaining steps of the prediction horizon.
State upper bounds, specified as a row vector of length
Nx or a matrix with
Nx columns, where
Nx is the number of states.
StateMax(:,i) replaces the States(i).Max
property of the controller at run time.
To use the same bounds across the prediction horizon, specify a row vector.
To vary the bounds over the prediction horizon from time k+1 to time k+p, specify a matrix with up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the final bounds are used for the remaining steps of the prediction horizon.
State function parameter values, specified as a vector with length equal to
the value of the Model.ParameterLength property of the
multistage controller object. If Model.StateFcn needs a
parameter vector, you must provide its value at runtime using this field. If
Model.ParameterLength is 0 this field does
not exist in the structure returned by
getSimulationData.
Stage functions parameter values, specified as a vector with length equal to
the sum of all the values in the Stages(i).ParameterLength
properties of the multistage controller object. If any cost or constraint function
defined in the Stages property needs a parameter vector, you
must provide all the parameter vectors at runtime (stacked in a single column)
using this field. If none of your stage functions have parameters, this field does
not exist in the structure returned by
getSimulationData.
You must stack the parameter vectors for all stages in the column vector
StateFcnParameters as
follows.
[parameter vector for stage 1; parameter vector for stage 2; ... parameter vector for stage p+1; ]
Terminal state, specified as a column vector with as many elements as the
number of states. The terminal state is the desired state at the last prediction
step. To specify desired terminal states at run-time via this field, you must
specify finite values in the TerminalState field of the
Model property of msobj. Specify
inf for the states that do not need to be constrained to a
terminal value. At run time, nlmpcmove ignores any values in the
TerminalState field of simdata that
correspond to inf values in msobj. If you
do not specify any terminal value condition in msobj, this
field is not created in simdata.
If there is no TerminalState in
simdata then the terminal state constraint (if present)
does not change at run time.
Initial guesses for the decision variables, specified as a column vector of
length equal to the sum of the lengths of all the decision variable vectors for
each stage. Good initial guesses are important since they help the solver to
converge to a solution faster. Therefore, when simulating a control loop by
calling nlmpcmove repeatedly in a loop, pass
simdata as an input argument (so initial guesses can be
used), and at the same time return an updated version of
simdata (with new initial guesses for the next control
interval) as an output argument.
You must be stack the initial guesses for all stages in the column vector
InitialGuess as
follows.
[state vector guess for stage 1; manipulated variable vector guess for stage 1; manipulated variable vector rate guess for stage 1; % if used slack variable vector guess for stage 1; % if used state vector guess for stage 2; manipulated variable vector guess for stage 2; manipulated variable vector rate guess for stage 2; % if used slack variable vector guess for stage 2; % if used ... state vector guess for stage p; manipulated variable vector guess for stage p; manipulated variable vector rate guess for stage p; % if used slack variable vector guess for stage p; % if used state vector guess for stage p+1; slack variable vector guess for stage p+1; % if used ]
If InitialGuess is [], the default
initial guesses are calculated from the x and
lastmv arguments passed to
nlmpcmove.
In general, during closed-loop simulation, you do not specify
InitialGuess yourself. Instead, when calling nlmpcmove, return the simdata output argument,
which contains the calculated initial guesses for the next control interval. You
can then pass simdata as an input argument to
nlmpcmove for the next control interval. These steps are a
best practice, even if you do not specify any other run-time options.
Tips
During closed-loop simulations, it is best practice to warm start the nonlinear solver by using the predicted state and manipulated variable trajectories from the previous control interval as the initial guesses for the current control interval. To use these trajectories as initial guesses:
Return the
optoutput argument when callingnlmpcmove. Thisnlmpcmoveoptobject contains any run-time options you specified in the previous call tonlmpcmove, along with the initial guesses for the state (opt.X0) and manipulated variable (opt.MV0) trajectories.Pass this object in as the
optionsinput argument tonlmpcmovefor the next control interval.
These steps are a best practice, even if you do not specify any other run-time options.
Version History
Introduced in R2018b
See Also
Functions
Objects
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Web サイトの選択
Web サイトを選択すると、翻訳されたコンテンツにアクセスし、地域のイベントやサービスを確認できます。現在の位置情報に基づき、次のサイトの選択を推奨します:
また、以下のリストから Web サイトを選択することもできます。
最適なサイトパフォーマンスの取得方法
中国のサイト (中国語または英語) を選択することで、最適なサイトパフォーマンスが得られます。その他の国の MathWorks のサイトは、お客様の地域からのアクセスが最適化されていません。
南北アメリカ
- América Latina (Español)
- Canada (English)
- United States (English)
ヨーロッパ
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)