Inverse Clarke Transform

Implement αβ to abc transformation

• 

Libraries:
Motor Control Blockset / Controls / Math Transforms
Motor Control Blockset HDL Support / Controls / Math Transforms

Description

The Inverse Clarke Transform block computes the Inverse Clarke transformation of balanced, two-phase orthogonal components in the stationary αβ reference frame and outputs the balanced, three-phase components in the stationary abc reference frame. Alternatively, the block can compute Inverse Clarke transformation of the components α, β, and 0 to output the three-phase components a, b, and c. For a balanced system, the zero component is equal to zero. Use the Number of inputs parameter to use either two or three inputs.

The block accepts the α-β axis components as inputs and outputs the corresponding three-phase signals, where the phase-a axis aligns with the α-axis.

• The α and β input components in the αβ reference frame.

  

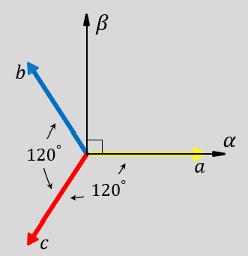
• The direction of the equivalent a, b, and c output components in the abc reference frame and the αβ reference frame.

  

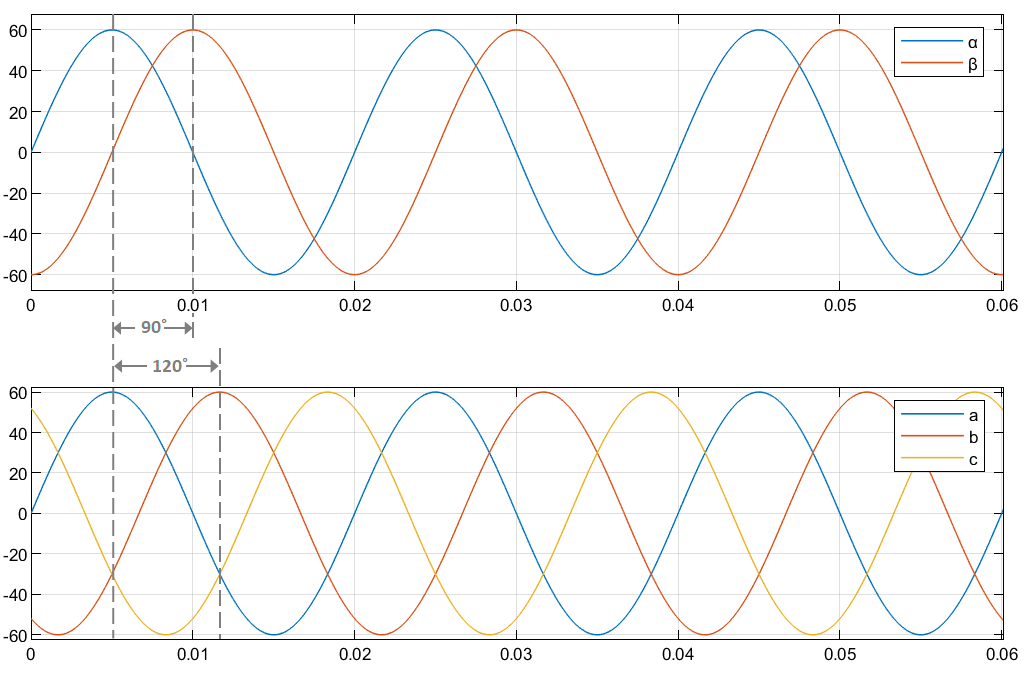
• The time-response of the individual components of equivalent balanced αβ and abc systems.

  

Equations

The following equation describes the Inverse Clarke transform computation:

$\left[\begin{array}{c}{f}_a\\ f_b\\ f_c\end{array}\right]=\left[\begin{array}{ccc}1& 0& 1\\ -\frac{1}{2}& \frac{\sqrt{3}}{2}& 1\\ -\frac{1}{2}& -\frac{\sqrt{3}}{2}& 1\end{array}\right]\left[\begin{array}{c}{f}_{\alpha }\\ f_{\beta }\\ f_0\end{array}\right]$

For balanced systems like motors, the zero sequence component calculation is always zero:

$$i_a+i_b+i_c=0$$

Therefore, you can use only two current sensors in three-phase motor drives, where you can calculate the third phase as,

$$i_c=-(i_a+i_b)$$

By using these equations, the block implements the Inverse Clarke transform as,

$$\left[\begin{array}{c}\begin{array}{c}{f}_{a }\\ f_{b }\end{array}\\ f_{c }\end{array}\right]=\left[\begin{array}{c}\begin{array}{cc}1& 0\\ -\frac{1}{2}& \frac{\sqrt{3}}{2}\\ -\frac{1}{2}& -\frac{\sqrt{3}}{2}\end{array}\end{array}\right]\left[\begin{array}{c}{f}_{\alpha }\\ f_{\beta }\end{array}\right]$$

where:

• $f_{\alpha }$ and $f_{\beta }$ are the balanced two-phase orthogonal components in the stationary αβ reference frame.

• $f_0$ is the zero component in the stationary αβ reference frame.

• $f_a$, $f_b$, and $f_c$ are the balanced three-phase components in the abc reference frame.

Ports

Input

α — Axis component

scalar

Alpha-axis component, α, in the stationary αβ reference frame.

Dependencies

To enable this port, set the Number of inputs parameter to Two inputs.

Data Types: single | double | fixed point

β — Axis component

scalar

Beta-axis component, β, in the stationary αβ reference frame.

Dependencies

To enable this port, set the Number of inputs parameter to Two inputs.

Data Types: single | double | fixed point

αβ0 — Axis components

scalar

Multiplexed alpha-axis component, α and beta-axis component, β and 0 component, in the stationary αβ reference frame.

Dependencies

To enable this port, set the Number of inputs parameter to Three inputs.

Data Types: single | double | fixed point

Output

a — Phase component

scalar

Component of the three-phase system in the abc reference frame.

Dependencies

To enable this port, set the Number of inputs parameter to Two inputs.

Data Types: single | double | fixed point

b — Phase component

scalar

Component of the three-phase system in the abc reference frame.

Dependencies

To enable this port, set the Number of inputs parameter to Two inputs.

Data Types: single | double | fixed point

c — Phase component

scalar

Component of the three-phase system in the abc reference frame.

Dependencies

To enable this port, set the Number of inputs parameter to Two inputs.

Data Types: single | double | fixed point

abc — Phase components

scalar

Multiplexed phase components a,b, and c of the three-phase system in the abc reference frame.

Dependencies

To enable this port, set the Number of inputs parameter to Three inputs.

Data Types: single | double | fixed point

Parameters

Number of inputs — Number of block inputs

Two inputs (default) | Three inputs

Select the number of inputs that you can specify:

• Two inputs — Configure the block to accept two separate input signals α and β. The block generates three separate output signals a, b, and c.

• Three inputs — Configure the block to accept a multiplexed input containing α, β, and 0 signals. The block generates a multiplexed output containing a,b, and c signals.

Power invariant — Enable power invariance

off (default) | on

To enable the power invariance property in the block output, select this parameter. To disable power invariance (enable amplitude invariance) in the block output, clear this parameter.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

HDL Code Generation

Generate VHDL, Verilog and SystemVerilog code for FPGA and ASIC designs using HDL Coder™.

HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic.

HDL Architecture

This block has one default HDL architecture.

HDL Block Properties

ConstrainedOutputPipeline	Number of registers to place at the outputs by moving existing delays within your design. Distributed pipelining does not redistribute these registers. The default is 0. For more details, see ConstrainedOutputPipeline (HDL Coder).
InputPipeline	Number of input pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is 0. For more details, see InputPipeline (HDL Coder).
OutputPipeline	Number of output pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is 0. For more details, see OutputPipeline (HDL Coder).

Fixed-Point Conversion
Design and simulate fixed-point systems using Fixed-Point Designer™.

Version History

Introduced in R2020a