unwrap
Shift phase angles
Description
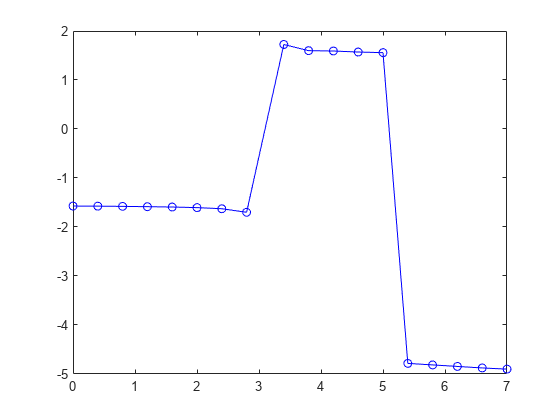
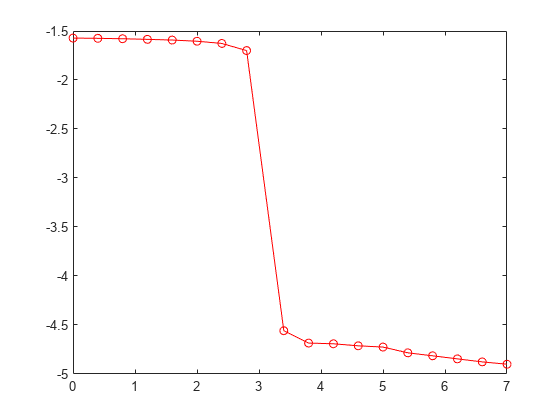
Q = unwrap( unwraps the radian phase angles
in a vector P)P. Whenever the jump between consecutive angles is greater
than or equal to π radians, unwrap shifts the angles
by adding multiples of ±2π until the jump is less than
π. If P is a matrix, unwrap
operates columnwise. If P is a multidimensional array,
unwrap operates on the first dimension whose size is larger than
1.
Examples
Input Arguments
Output Arguments
Extended Capabilities
Version History
Introduced before R2006a

![unwrap(P,[],1) column-wise operation](unwrap_dim_1.png)
![unwrap(P,[],2) row-wise operation](unwrap_dim_2.png)
