smoothdata2
Syntax
Description
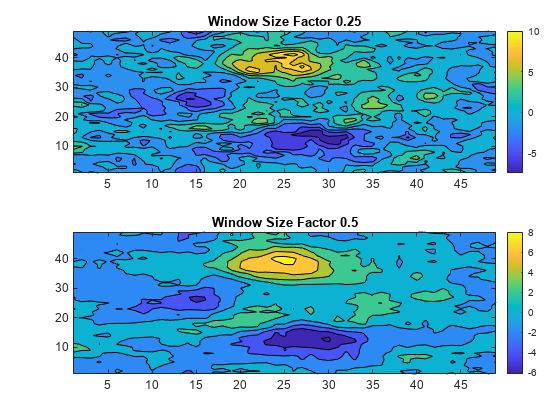
S = smoothdata2(___,Name=Value)smoothdata2(A,SmoothingFactor=0.5) adjusts the level of
smoothing by specifying a factor that scales the window size that
smoothdata2 determines from the entries in A.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
Algorithms
When the window size for the smoothing method is not specified,
smoothdata2 computes a default window size based on a heuristic. For a
smoothing factor τ, the heuristic estimates a moving average window size that attenuates
approximately 100*τ percent of the energy of the input data.
Version History
Introduced in R2023b
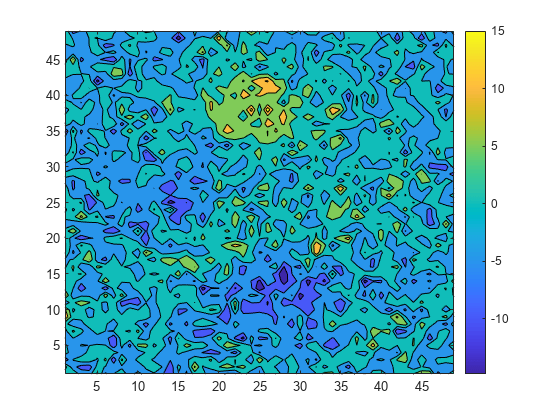


![Given elements 1 to 7, if the current sample point is 4, then the corresponding window spans the range [2, 6].](movwindow_vector.png)
![Given elements 1 to 7, if the current sample point is 2, then the corresponding window spans the range [1, 4].](movwindow_edgetruncate.png)
![Given elements 1 to 7, if the current sample point is 2, then the corresponding window spans the range [1, 5].](movwindow_edgeslide.png)