Main Content

mcxGate

Multi-controlled X gate

Since R2023a

collapse all in page

Installation Required: This functionality requires MATLAB Support Package for Quantum Computing.

Syntax

cg = mcxGate(controlQubits,targetQubit,ancillaQubits)

Description

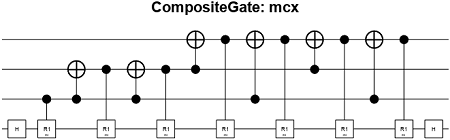
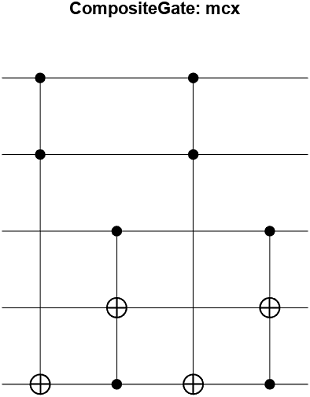
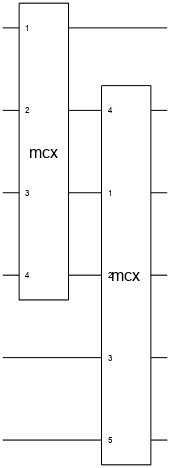
cg = mcxGate(controlQubits,targetQubit,ancillaQubits) applies a multi-controlled X (MCX) gate. This gate operates on a single target qubit based on the states of the control qubits, with a number of ancilla qubits that do not affect the operation. If all control qubits are in the |1〉 state, then this gate applies a Pauli X gate (xGate or the equivalent classical NOT gate) to the target qubit. Otherwise, the gate has no effect on the target qubit.

The qubit indices in controlQubits, targetQubit, and ancillaQubits must not be the same.

example

Examples

collapse all

Create an MCX gate with three control qubits, one target qubit, and no ancilla qubits.

cg = mcxGate(1:3,4,[])
cg = 

  CompositeGate with properties:

             Name: "mcx"
    ControlQubits: [1×0 double]
     TargetQubits: [4×1 double]
            Gates: [15×1 quantum.gate.SimpleGate]

Plot the returned MCX gate to show its 15 internal gates. This MCX gate consists of two Hadamard gates, seven R1 gates, and six controlled X gates (CNOT gates). The Hadamard gates at the beginning and end of the internal gates are used to transform the state of the target qubit from the Z basis to the X basis and from the X basis to the Z basis.

plot(cg)

Internal gates of the mcx composite gate with three control qubits, one target qubit, and no ancilla qubits

Get the matrix representation of this MCX gate. Because the matrix operations for the internal gates accumulate machine precision errors, round the matrix representation of this gate for clarity.

M = round(getMatrix(cg),8)
M =

     1     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0
     0     1     0     0     0     0     0     0     0     0     0     0     0     0     0     0
     0     0     1     0     0     0     0     0     0     0     0     0     0     0     0     0
     0     0     0     1     0     0     0     0     0     0     0     0     0     0     0     0
     0     0     0     0     1     0     0     0     0     0     0     0     0     0     0     0
     0     0     0     0     0     1     0     0     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     1     0     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     1     0     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0     1     0     0     0     0     0     0     0
     0     0     0     0     0     0     0     0     0     1     0     0     0     0     0     0
     0     0     0     0     0     0     0     0     0     0     1     0     0     0     0     0
     0     0     0     0     0     0     0     0     0     0     0     1     0     0     0     0
     0     0     0     0     0     0     0     0     0     0     0     0     1     0     0     0
     0     0     0     0     0     0     0     0     0     0     0     0     0     1     0     0
     0     0     0     0     0     0     0     0     0     0     0     0     0     0     0     1
     0     0     0     0     0     0     0     0     0     0     0     0     0     0     1     0

Create an MCX gate with three control qubits, one target qubit, and one ancilla qubit.

cg = mcxGate(1:3,4,5)
cg = 

  CompositeGate with properties:

             Name: "mcx"
    ControlQubits: [1×0 double]
     TargetQubits: [5×1 double]
            Gates: [4×1 quantum.gate.SimpleGate]

Plot the returned MCX gate to show its four internal gates. This MCX gate consists of four controlled controlled X gates (CCX or CCNOT gates). The implementation of the MCX gate with one ancilla qubit requires fewer gates than the implementation with no ancilla qubits.

plot(cg)

Internal gates of the mcx composite gate with one ancilla qubit

Create a quantum circuit that consists of two MCX gates. The first MCX gate has control qubits with indices 1 to 3 and a target qubit with index 4 (without any ancilla qubits). The second MCX gate has control qubits with indices 3 to 5, a target qubit with index 2, and an ancilla qubit with index 6.

gates = [mcxGate(1:3,4,[]); mcxGate(3:5,2,6)];
c = quantumCircuit(gates)
c = 

  quantumCircuit with properties:

    NumQubits: 6
        Gates: [2×1 quantum.gate.CompositeGate]
         Name: ""

Plot the quantum circuit.

plot(c)

Quantum circuit with two mcx gates

The plotted circuit consists of six qubits with indices 1 to 6. The plot shows that qubits 1 to 4 of the outer circuit are mapped to qubits 1 to 4 of the inner circuit of internal gates that construct the first MCX gate. For the second MCX gate, qubit 2 of the outer circuit is mapped to qubit 4 of the inner circuit, qubits 3 to 5 of the outer circuit are mapped to qubits 1 to 3 of the inner circuit, and qubit 6 of the outer circuit is mapped to qubit 5 of the inner circuit.

Click the second MCX gate in the plot. A new figure showing the internal gates of the composite gate appears.

Internal gates of the second mcx composite gate

Input Arguments

collapse all

Control qubits of the MCX gate, specified as a positive integer scalar index or vector of qubit indices.

Target qubit of the MCX gate, specified as a positive integer scalar index.

Ancilla qubits of the MCX gate, specified as a positive integer scalar index or vector of qubit indices.

The number of ancilla qubits (or length(ancillaQubits)) determines the implementation of the internal gates to construct the returned CompositeGate object for the MCX gate, but it does not affect the MCX gate operation on the target qubit.

  • If the number of ancilla qubits is 1 (recommended), then the implementation requires a linear number of internal gates with respect to the number of control qubits.

  • If the number of ancilla qubits is k–2, where k is the number of control qubits, then the implementation requires the minimal number of internal gates among these options. The number of internal gates still grows linearly with respect to the number of control qubits, but at a smaller factor compared to the option with one ancilla qubit.

  • If the number of ancilla qubits is 0, then the implementation requires an exponential number of internal gates with respect to the number of control qubits.

All implementations assume the ancilla qubits are in an arbitrary state, and the MCX gate returns the ancilla qubits in the same state that they started in.

Output Arguments

collapse all

MCX gate, returned as a CompositeGate object or a SimpleGate object.

  • If the number of control qubits is greater than 2 (length(controlQubits)>2), then the mcxGate function returns cg as a CompositeGate object that consists of several internal gates.

  • If the number of control qubits is less than or equal to 2 (length(controlQubits)<=2), then the mcxGate function returns cg as a SimpleGate object. If there are no control qubits, then the function returns cg as the X gate (xGate). If there is one control qubit, then the function returns cg as the controlled X or CNOT gate (cxGate). If there are two control qubits, then the function returns cg as the CCNOT gate (ccxGate).

References

[1] Barenco, Adriano, et al. “Elementary Gates for Quantum Computation.” Physical Review A 52, no. 5 (November 1, 1995): 3457–67. https://doi.org/10.1103/PhysRevA.52.3457.

Version History

Introduced in R2023a

See Also

| | | | |

Topics