lsqminnorm

線形方程式の最小ノルムの最小二乗解

構文

X = lsqminnorm(A,B)

X = lsqminnorm(A,B,tol)

X = lsqminnorm(___,rankWarn)

X = lsqminnorm(___,RegularizationFactor=alpha)

説明

X = lsqminnorm(A,B) は、線形方程式 AX = B を解き、norm(A*X-B) の値を最小化する配列 X を返します。複数の解が存在する場合、lsqminnorm は norm(X) を最小化する解を返します。B に複数の列がある場合、前述のステートメントは X と B それぞれの各列について真になります。

X = lsqminnorm(A,B,tol) はさらに、lsqminnorm が A のランクを判別するために使用する許容誤差を指定します。

X = lsqminnorm(___,rankWarn) は、A のランクが低い場合に警告を表示するかどうかを指定します。前述の構文にある任意の入力引数の組み合わせに加えてこのオプションを指定できます。rankWarn は "nowarn" (既定値) または "warn" のいずれかにできます。

X = lsqminnorm(___,RegularizationFactor=alpha) は、解 X に適用する Tikhonov 正則化係数を指定します。 (R2024b 以降)

例

無限の解をもつ線形システムの求解

解が無限に存在する線形システムの解を、バックスラッシュ (\) と lsqminnorm を使用して求めます。解の 2 ノルムを使用して結果を比較します。

$\mathrm{Ax}=\mathit{b}$ の解が無限に存在する場合、それぞれの解が $\Vert \mathrm{Ax}-\mathit{b}\Vert$ を最小化します。バックスラッシュ コマンド (\) はそのような解の 1 つを計算しますが、通常この解は $\Vert \mathit{x}\Vert$ を最小化しません。lsqminnorm により計算される解は、norm(A*x-b) だけでなく norm(x) も最小化します。

1 つの方程式と 2 つの未知数からなる単純な線形システム $2{\mathit{x}}_1+3{\mathit{x}}_2=8$ を考えてみます。方程式の数が未知数の数より少ないため、このシステムは "劣決定" です。バックスラッシュと lsqminnorm の両方を使用してこの方程式を解きます。

A = [2 3];
b = 8;
x_a = A\b

x_a = 2×1

         0
    2.6667

x_b = lsqminnorm(A,b)

x_b = 2×1

    1.2308
    1.8462

これらの 2 つの方法では求められる解が異なります。バックスラッシュは norm(A*x-b) を最小化するだけですが、lsqminnorm は norm(x) も最小化します。これらのノルムを計算し、比較しやすいように結果を table に格納します。

s1 = {'Backslash'; 'lsqminnorm'};
s2 = {'norm_Ax_minus_b','norm_x'};
T = table([norm(A*x_a-b); norm(A*x_b-b)],[norm(x_a); norm(x_b)],'RowNames',s1,'VariableNames',s2)

T=2×2 table
                  norm_Ax_minus_b    norm_x
                  _______________    ______

    Backslash                0       2.6667
    lsqminnorm      8.8818e-16       2.2188

次の図はこの内容を説明するもので、それぞれの方法でどの解が返されるかを示しています。青のラインは、方程式 ${\mathit{x}}_2=-\frac{2}{3}{\mathit{x}}_1+\frac{8}{3}$ の解の数が無限であることを示しています。オレンジ色の丸は、原点から解のラインまでの最小距離を表します。lsqminnorm が返す解はこのラインと円の接点と完全に一致します。これは、この解が原点に最も近い解であることを表します。

ノイズが多いデータの影響の低減

lsqminnorm では、ランク計算の許容誤差、または解の Tikhonov 正則化係数を指定できます。これらの仕様は、ランダム ノイズによって解に悪影響が出ないように、問題の規模を定義するのに役立ちます。

ランク 5 の低ランク行列 A と右辺のベクトル b を作成します。

U = randn(200,5);
V = randn(100,5);
A = U*V';
b = U*randn(5,1) + 1e-4*randn(200,1);

lsqminnorm を使用して線形システム $\mathrm{Ax}=\mathit{b}$ を解きます。A*x-b と x のノルムを計算して、解の質を確認します。

x = lsqminnorm(A,b);
norm(A*x-b)

ans = 
0.0014

norm(x)

ans = 
0.1741

次に、行列 A に少量のノイズを追加し、もう一度この線形システムを解きます。このノイズは線形システムの解ベクトル x に過剰に影響しています。

Anoise = A + 1e-12*randn(200,100);
xnoise = lsqminnorm(Anoise,b);
norm(Anoise*xnoise - b)

ans = 
0.0010

norm(xnoise)

ans = 
1.1215e+08

解が大きく異なる理由は、ノイズが A の低ランク近似に影響しているためです。つまり、lsqminnorm は、A の QR 分解で R 行列の対角にある小さな値を実際より重要なものとして扱います。R の対角にある小さな値は、0 として扱われるのが理想的です。

Anoise の QR 分解で R 行列の対角要素をプロットします。対角要素の多くで、次数が 1e-10 です。

[Q,R,p] = qr(Anoise,0);
semilogy(abs(diag(R)),"o")

lsqminnorm で使用される許容誤差を大きくして、誤差が 1e-8 未満の Anoise の低ランク近似が計算で使用されるようにします。許容誤差を大きくすることで、結果に対するノイズの影響がはるかに小さくなります。許容誤差を使用して得られる解は、元の解 x に非常に近いものです。

xtol = lsqminnorm(Anoise,b,1e-8);
norm(Anoise*xtol - b)

ans = 
0.0014

norm(xtol)

ans = 
0.1741

norm(x - xtol)

ans = 
1.0811e-14

あるいは、Tikhonov 正則化係数として 1 を指定します。ノイズが関係する問題など、悪条件の問題では、過適合が生じないように正則化係数を指定できます。

xreg = lsqminnorm(Anoise,b,RegularizationFactor=1);
norm(Anoise*xreg - b)

ans = 
0.0018

norm(xreg)

ans = 
0.1741

norm(x - xreg)

ans = 
7.9359e-06

低ランク行列の警告の切り替え

警告が有効になっている状態で、低ランク係数行列を含む線形システムを解きます。

ランク 2 の 3 行 3 列の行列を作成します。この行列で最初の 2 列を同時に追加すると、3 列目を取得できます。

A = [1 2 3; 4 5 9; 6 7 13]

A = 3×3

     1     2     3
     4     5     9
     6     7    13

問題 $\mathrm{Ax}=\mathit{b}$ の最小ノルムの最小二乗解を求めます。ここで $\mathit{b}$ は $\mathit{A}$ の 2 列目と等しくなります。lsqminnorm の 'warn' フラグを指定すると、A が低ランクであることが検出された場合に警告が表示されます。

b = A(:,2);
x = lsqminnorm(A,b,'warn')

Warning: Rank deficient, rank = 2, tol =  1.072041e-14.

x = 3×1

   -0.3333
    0.6667
    0.3333

入力引数

A — 係数行列

行列

係数行列。係数行列は連立線形方程式で左辺に Ax = B として表示されます。係数行列は完全とスパースのどちらかにできます。

データ型: double | single
複素数のサポート: あり

B — 入力配列

ベクトル | 行列

入力配列。ベクトルまたは行列として指定します。B は連立線形方程式で左辺に Ax = B として表示されます。B が行列の場合、この行列の各列は右辺の各ベクトルを表します。

データ型: double | single
複素数のサポート: あり

tol — ランクの許容誤差

非負のスカラー

ランクの許容誤差。非負のスカラーとして指定します。許容誤差を指定すると、解が係数行列のランダム ノイズの影響を受けにくくなります。既定では、lsqminnorm は A の QR 分解に基づいて tol を計算します。

lsqminnorm は A のランクを、QR 分解 [Q,R,p] = qr(A,0) の行列 R において絶対値が tol より大きい対角要素の数として計算します。A のランクが k の場合、この関数は Q の最初の k 列に R の最初の k 行を乗算して、A の低ランク近似を形成します。許容誤差を変更すると、A の低ランク近似に影響します。

例: X = lsqminnorm(A,B,1e-2)

データ型: double

rankWarn — 低ランク行列の警告の切り替え

"nowarn" (既定値) | "warn"

低ランク行列の警告の切り替え。"nowarn" または "warn" として指定します。"warn" を指定すると、lsqminnorm は係数行列 A がランク落ちしている場合に警告を生成します。

例: X = lsqminnorm(A,B,"warn")

alpha — Tikhonov 正則化係数

0 (既定値) | 実数

R2024b 以降

最小二乗解の Tikhonov 正則化係数。実数として指定します。正則化係数を alpha として指定すると、X の各列について norm(A*X-B)^2 + alpha^2*norm(X)^2 を最小化するような解 X が返されます。悪条件の問題の場合、正則化係数を指定すると、ノルムが小さい解が優先されます。

データ型: double | single

ヒント

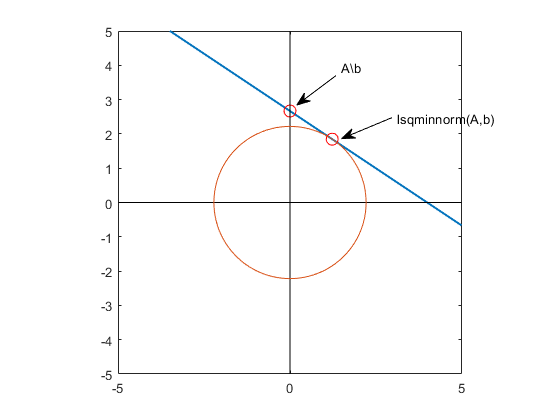
• lsqminnorm が計算する最小ノルム解は、解が複数ある場合に重要です。方程式 Ax = b は、A が劣決定 (行の数が列より少ない) であるか低ランクである場合、解が多数あります。

• lsqminnorm(A,B,tol) は通常、pinv(A,tol)*B と比べて、線形システムの最小ノルムの最小二乗解を効率的に計算できます。lsqminnorm は完全直交分解 (COD) を使用して A の低ランク近似を求めますが、pinv は特異値分解 (SVD) を使用します。そのため、pinv と lsqminnorm の結果は完全には一致しません。

• スパース行列では、lsqminnorm は密行列と異なるアルゴリズムを使用するため、結果も異なります。

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

• コード生成では、この関数のスパース行列入力はサポートされません。

スレッドベースの環境

MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。 (R2024b 以降)

lsqminnorm 関数は GPU 配列入力をサポートしますが、次の使用上の注意および制限があります。

• 係数行列 A は非スパースでなければなりません。

詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2017b で導入

R2025a: regularizationFactor のコード生成のサポート

コード生成で、lsqminnorm への入力として regularizationFactor がサポートされます。

R2024b: 最小二乗解への Tikhonov 正則化の適用

Tikhonov 正則化係数 alpha を指定して、X の各列について norm(A*X-B)^2 + alpha^2*norm(X)^2 を最小化するような解 X を返すことができます。

参考

pagelsqminnorm | pinv | decomposition | mldivide

トピック

• 連立線形方程式