inpolygon
多角形領域の内側またはエッジ上の点
説明
例
五角形と一連の点を定義します。そして、どの点が五角形の内側 (またはエッジ上) に存在するか判別します。
多角形の頂点の x 座標と y 座標を定義して五角形を作成します。
L = linspace(0,2*pi,6); xv = cos(L)'; yv = sin(L)';
250 個のランダムなクエリ点の x 座標と y 座標を定義します。乱数発生器を初期化して randn の出力を反復可能にします。
rng default
xq = randn(250,1);
yq = randn(250,1);各点が多角形領域の内側またはエッジ上にあるかどうか判定します。また、いずれかの点が多角形領域のエッジ上にあるかどうか判定します。
[in,on] = inpolygon(xq,yq,xv,yv);
多角形領域の内側またはエッジ上にある点の数を求めます。
numel(xq(in))
ans = 80
多角形領域のエッジ上にある点の数を求めます。
numel(xq(on))
ans = 0
多角形領域のエッジ上に点は存在しないため、xq(in), yq(in) で特定される 80 個の点はすべて厳密に多角形領域の内側にあります。
多角形領域の外側にある (内側やエッジ上ではない) 点の数を求めます。
numel(xq(~in))
ans = 170
多角形とクエリ点をプロットします。多角形の内側の点を赤いプラス記号で表示します。多角形の外側の点を青い円で表示します。
figure plot(xv,yv) % polygon axis equal hold on plot(xq(in),yq(in),'r+') % points inside plot(xq(~in),yq(~in),'bo') % points outside hold off
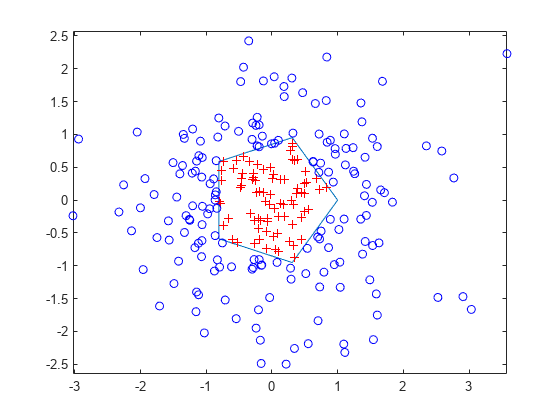
正方形の穴をもつ正方形の内側の点を検出します。
正方形の穴をもつ正方形の領域を定義します。外側のループの頂点を反時計回りの方向で指定し、内側のループの頂点を時計回りの方向で指定します。NaN を使用して外側のループと内側のループの座標を分離します。
xv = [1 4 4 1 1 NaN 2 2 3 3 2]; yv = [1 1 4 4 1 NaN 2 3 3 2 2];
500 個のランダムな点の x 座標と y 座標を定義します。乱数発生器を初期化して randn の出力を反復可能にします。
rng default
xq = rand(500,1)*5;
yq = rand(500,1)*5;各点が多角形領域の内側またはエッジ上にあるかどうか判定します。
in = inpolygon(xq,yq,xv,yv);
多角形とクエリ点をプロットします。多角形の内側の点を赤いプラス記号で表示します。多角形の外側の点を青い円で表示します。
figure plot(xv,yv,'LineWidth',2) % polygon axis equal hold on plot(xq(in),yq(in),'r+') % points inside plot(xq(~in),yq(~in),'bo') % points outside hold off

正方形の穴の中のクエリ点は多角形の外側にあります。
星形五角形の x 座標と y 座標を定義します。
xv = [0.5;0.2;1.0;0;0.8;0.5]; yv = [1.0;0.1;0.7;0.7;0.1;1];
12 個のクエリ点の x 座標と y 座標を定義します。
xq = [0.1;0.5;0.9;0.2;0.4;0.5;0.5;0.9;0.6;0.8;0.7;0.2]; yq = [0.4;0.6;0.9;0.7;0.3;0.8;0.2;0.4;0.4;0.6;0.2;0.6];
各点が多角形領域の内側またはエッジ上にあるかどうか判定します。また、いずれかの点が多角形領域のエッジ上にあるかどうか判定します。
[in,on] = inpolygon(xq,yq,xv,yv);
多角形領域の内側またはエッジ上にある点の数を求めます。
numel(xq(in))
ans = 8
多角形領域のエッジ上にある点の数を求めます。
numel(xq(on))
ans = 2
多角形領域の外側にある (内側やエッジ上ではない) 点の数を求めます。
numel(xq(~in))
ans = 4
多角形と点をプロットします。多角形の厳密に内側の点を赤いプラス記号で表示します。エッジ上の点を黒いアスタリスクで表示します。多角形の外側の点を青い円で表示します。
figure plot(xv,yv) % polygon hold on plot(xq(in&~on),yq(in&~on),'r+') % points strictly inside plot(xq(on),yq(on),'k*') % points on edge plot(xq(~in),yq(~in),'bo') % points outside hold off
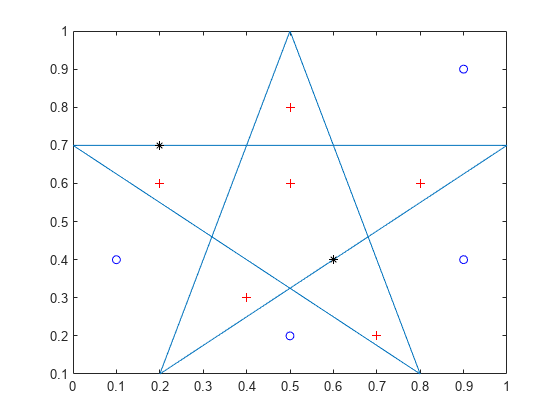
6 つの点が多角形の内側にあります。2 つの点が多角形のエッジ上にあります。4 つの点が多角形の外側にあります。
入力引数
クエリ点の x 座標。スカラー、ベクトル、行列または多次元配列として指定します。
xq のサイズは yq のサイズと同じでなければなりません。
データ型: double | single
クエリ点の y 座標。スカラー、ベクトル、行列または多次元配列として指定します。
yq のサイズは xq のサイズと同じでなければなりません。
データ型: double | single
多角形の頂点の x 座標。ベクトルとして指定します。
xv のサイズは yv のサイズと同じでなければなりません。
複数結合された多角形または結合されていない多角形の頂点を指定するには、NaN を使って個々のループの座標を分離します。また、複数結合された多角形では、外側のループと内側のループの頂点の向きを反対方向にしなければなりません。
自己交差やループの向きがあいまいなため、自己交差する複数結合の多角形になることはできません。
データ型: double | single
多角形の頂点の y 座標。ベクトルとして指定します。
yv のサイズは xv のサイズと同じでなければなりません。
複数結合された多角形または結合されていない多角形の頂点を指定するには、NaN を使って個々のループの座標を分離します。また、複数結合された多角形では、外側のループと内側のループの頂点の向きを反対方向にしなければなりません。
自己交差やループの向きがあいまいなため、自己交差する複数結合の多角形になることはできません。
データ型: double | single
出力引数
多角形領域の内側またはエッジ上の点のインジケーター。logical 配列として返されます。in は xq および yq と同じサイズになります。
logical
1(true) は、対応するクエリ点が多角形領域の内側または多角形の境界のエッジ上にあることを示します。logical
0(false) は、対応するクエリ点が多角形領域の外側にあることを示します。
このため、in を xq および yq のインデックス付けに使用して、対象のクエリ点を特定できます。
xq(in), yq(in) | 多角形領域の内側またはエッジ上のクエリ点 |
xq(~in), yq(~in) | 多角形領域の外側のクエリ点 |
多角形領域のエッジ上の点のインジケーター。logical 配列として返されます。on は xq および yq と同じサイズになります。
logical
1(true) は、対応するクエリ点が多角形の境界上にあることを示します。logical
0(false) は、対応するクエリ点が多角形の境界の内側または外側にあることを示します。
このため、on と in を xq および yq のインデックス付けに使用して、対象のクエリ点を特定できます。
xq(on), yq(on) | 多角形境界上のクエリ点 |
xq(~on), yq(~on) | 多角形の境界の内側または外側のクエリ点 |
xq(in&~on), yq(in&~on) | 多角形領域の厳密に内側のクエリ点 |
拡張機能
使用上の注意および制限:
単精度入力と倍精度入力はサポートされますが、すべての入力が単精度であっても倍精度の演算が使用されます。
この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。
inpolygon 関数は、GPU 配列を完全にサポートします。GPU 上で関数を実行するには、入力データを gpuArray (Parallel Computing Toolbox) として指定します。詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。
この関数は分散配列を完全にサポートしています。詳細については、分散配列を使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。
バージョン履歴
R2006a より前に導入
参考
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Web サイトの選択
Web サイトを選択すると、翻訳されたコンテンツにアクセスし、地域のイベントやサービスを確認できます。現在の位置情報に基づき、次のサイトの選択を推奨します:
また、以下のリストから Web サイトを選択することもできます。
最適なサイトパフォーマンスの取得方法
中国のサイト (中国語または英語) を選択することで、最適なサイトパフォーマンスが得られます。その他の国の MathWorks のサイトは、お客様の地域からのアクセスが最適化されていません。
南北アメリカ
- América Latina (Español)
- Canada (English)
- United States (English)
ヨーロッパ
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)