centrality

ノードの重要度を測定

構文

C = centrality(G,type)

C = centrality(___,Name,Value)

説明

C = centrality(G,type) は、グラフ内の各ノードについて、type で指定されたノードの中心性を計算します。

C = centrality(___,Name,Value) は、1 つ以上の名前と値のペアの引数で指定された追加のオプションを使用します。たとえば、centrality(G,'closeness','Cost',c) は各エッジの通過コストを指定します。

例

6 つの Web サイトのページ ランク

架空の 6 件の Web サイトを含むグラフを作成し、プロットします。

s = [1 1 2 2 3 3 3 4 5];
t = [2 5 3 4 4 5 6 1 1];
names = {'http://www.example.com/alpha', 'http://www.example.com/beta', ...
         'http://www.example.com/gamma', 'http://www.example.com/delta', ...
         'http://www.example.com/epsilon', 'http://www.example.com/zeta'};
G = digraph(s,t,[],names);
plot(G,'NodeLabel',{'alpha','beta','gamma','delta','epsilon','zeta'})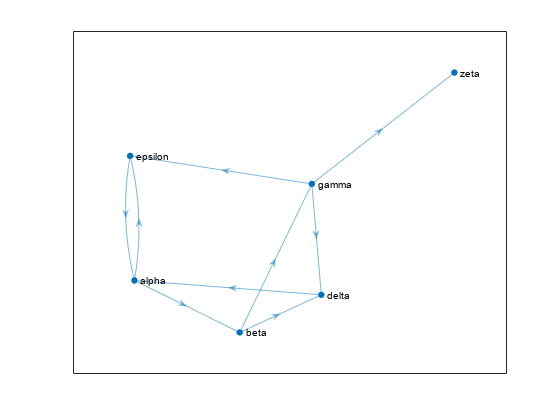

関数 centrality を使用して、各 Web サイトのページ ランクを計算します。この情報を、グラフの Nodes table にグラフ ノードの属性として追加します。

pg_ranks = centrality(G,'pagerank')

pg_ranks = 6×1

    0.3210
    0.1706
    0.1066
    0.1368
    0.2008
    0.0643

G.Nodes.PageRank = pg_ranks;
G.Nodes

ans=6×2 table
                   Name                   PageRank
    __________________________________    ________

    {'http://www.example.com/alpha'  }    0.32098 
    {'http://www.example.com/beta'   }    0.17057 
    {'http://www.example.com/gamma'  }    0.10657 
    {'http://www.example.com/delta'  }    0.13678 
    {'http://www.example.com/epsilon'}    0.20078 
    {'http://www.example.com/zeta'   }    0.06432 

また、centrality を使用してハブとオーソリティのノードを判別し、そのスコアを Nodes table に追加します。

hub_ranks = centrality(G,'hubs');
auth_ranks = centrality(G,'authorities');
G.Nodes.Hubs = hub_ranks;
G.Nodes.Authorities = auth_ranks;

G.Nodes

ans=6×4 table
                   Name                   PageRank       Hubs       Authorities
    __________________________________    ________    __________    ___________

    {'http://www.example.com/alpha'  }    0.32098        0.24995    7.3237e-05 
    {'http://www.example.com/beta'   }    0.17057        0.24995      0.099993 
    {'http://www.example.com/gamma'  }    0.10657        0.49991      0.099993 
    {'http://www.example.com/delta'  }    0.13678     9.1536e-05       0.29998 
    {'http://www.example.com/epsilon'}    0.20078     9.1536e-05       0.29998 
    {'http://www.example.com/zeta'   }    0.06432              0       0.19999 

乱数グラフの次数中心性

乱数のスパース隣接行列を使用して重み付きグラフを作成し、プロットします。エッジが多数あるため、EdgeAlpha に非常に小さい値を使用して、エッジをほぼ透明にします。

A = sprand(1000,1000,0.15);
A = A + A';
G = graph(A,'omitselfloops');
p = plot(G,'Layout','force','EdgeAlpha',0.005,'NodeColor','r');

各ノードの次数中心性を計算します。エッジの重みを使用して、各エッジの重要度を指定します。

deg_ranks = centrality(G,'degree','Importance',G.Edges.Weight);

discretize を使用して、中心性スコアを基にノードを 7 つの等間隔のビンに入れます。

edges = linspace(min(deg_ranks),max(deg_ranks),7);
bins = discretize(deg_ranks,edges);

プロット内の各ノードのサイズを、その中心性スコアに比例するように指定します。各ノードのマーカー サイズは、ビン番号 (1 ～ 7) に等しくなります。

p.MarkerSize = bins;

ミネソタ州の道路の近接性と媒介性

ミネソタ州の道路網を表すグラフ オブジェクト G が含まれている、minnesota.mat のデータを読み込みます。グラフ ノードは xy 座標をもち、G.Nodes table の変数 XCoord と変数 YCoord に格納されています。

load minnesota.mat
xy = [G.Nodes.XCoord G.Nodes.YCoord];

道路の長さにほぼ対応するエッジの重みをグラフに追加します。これは、各エッジの終了ノードの xy 座標間におけるユークリッド距離を使用して算出します。

[s,t] = findedge(G);
G.Edges.Weight = hypot(xy(s,1)-xy(t,1), xy(s,2)-xy(t,2));

ノードの xy 座標を使用してグラフをプロットします。

p = plot(G,'XData',xy(:,1),'YData',xy(:,2),'MarkerSize',5);
title('Minnesota Road Network')

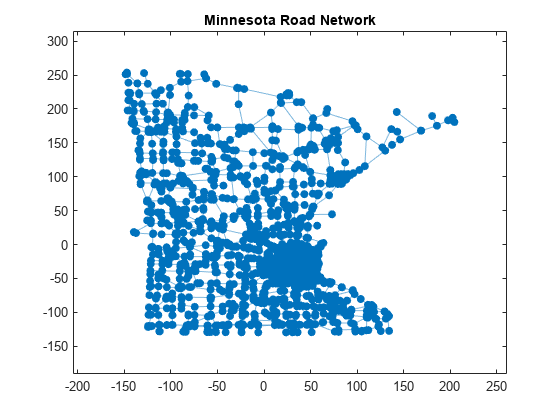
各ノードの近接中心性を計算します。ノードの色 NodeCData を、中心性スコアに比例するようにスケーリングします。

ucc = centrality(G,'closeness');
p.NodeCData = ucc;
colormap jet
colorbar
title('Closeness Centrality Scores - Unweighted')

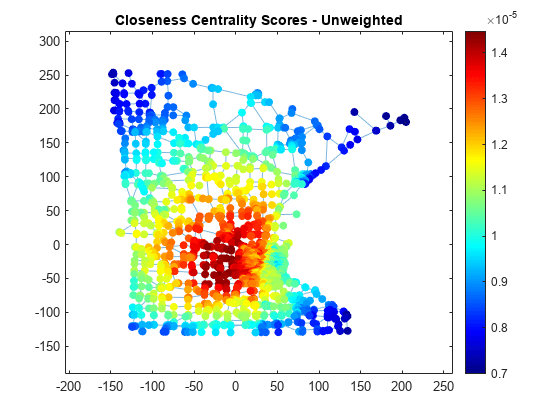
また、各エッジを通過するコストとしてエッジの重みを使用し、重み付きの近接中心性スコアを計算します。道路の長さをエッジの重みとして使用することにより、スコアの質が向上します。これは、移動したエッジ数ではなく、移動したすべてのエッジの合計長さとして距離が測定されるからです。

wcc = centrality(G,'closeness','Cost',G.Edges.Weight);
p.NodeCData = wcc;
title('Closeness Centrality Scores - Weighted')

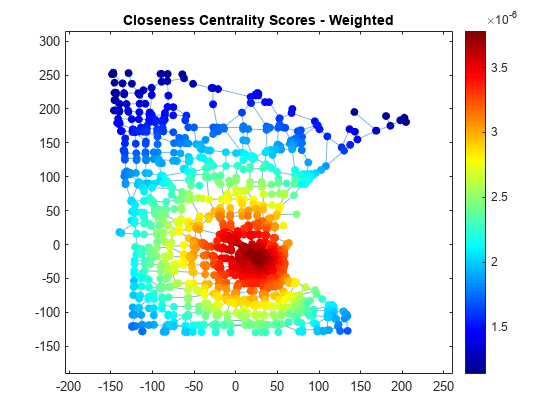
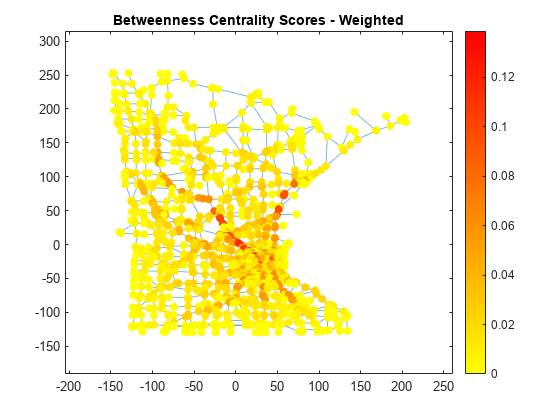
グラフで重み付き媒介中心性スコアを計算して、2 つのノード間の最短経路で最も頻繁に検出される道路を判定します。2 つのランダムなノード間の最短経路を通る旅行者が特定のノードを経由する確率をスコアが表すように、係数 $$\frac{(n-2)(n-1)}{2}$$ を使用して中心性スコアを正規化します。このプロットは、都市に出入りする非常に重要な道路がいくつかあることを示します。

wbc = centrality(G,'betweenness','Cost',G.Edges.Weight);
n = numnodes(G);
p.NodeCData = 2*wbc./((n-2)*(n-1));
colormap(flip(autumn,1));
title('Betweenness Centrality Scores - Weighted')

入力引数

G — 入力グラフ

graph オブジェクト | digraph オブジェクト

入力グラフ。graph オブジェクトまたは digraph オブジェクトとして指定します。無向グラフの作成には graph を、有向グラフの作成には digraph を使用します。

例: G = graph(1,2)

例: G = digraph([1 2],[2 3])

type — ノードの中心性のタイプ

'degree' | 'outdegree' | 'indegree' | 'closeness' | 'incloseness' | 'outcloseness' | 'betweenness' | 'pagerank' | 'eigenvector' | 'hubs' | 'authorities'

ノードの中心性のタイプ。次の表のいずれかのオプションとして指定します。この表には、各タイプで使用できる、適合性のある名前と値の引数も示されています。ノードのさまざまな中心性は、グラフにおけるノードの重要性を異なる測定を表しています。

オプション	グラフ タイプ	説明	名前と値の引数
'degree'	無向	'degree'、'outdegree' および 'indegree' の各中心性タイプは、各ノードに連結しているエッジ数に基づいています。 'degree' — 各ノードに連結しているエッジの数。自己ループはノードに連結している 2 本のエッジとしてカウントされます。 'indegree' — 各ノードに入るエッジ数。自己ループは、1 つの入方向のエッジとしてカウントされます。 'outdegree' — 各ノードから出るエッジ数。自己ループは、1 つの出方向のエッジとしてカウントされます。 エッジの重みに 'Importance' を指定した場合、アルゴリズムは連結エッジ数ではなく、エッジの重みの合計を使用します。	'Importance'
'indegree' 'outdegree'	有向
'closeness'	無向	'closeness'、'incloseness' および 'outcloseness' の各中心性タイプでは、グラフ内のあるノードから他のすべてのノードまでの距離を合計した値の逆数を使用します。到達できないノードがある場合、ノード i の中心性は次のように表されます。 $$c\left(i\right)={\left(\frac{A_i}{N-1}\right)}^2\frac{1}{C_i}.$$ Ai はノード i から到達可能なノードの数 (i はカウントしない)、N は G 内のノード数、Ci はノード i から到達可能なすべてのノードまでの距離の合計です。 ノード i から到達可能なノードがない場合、c(i) はゼロとなります。 'incloseness' の場合、距離測定はすべてのノードからノード i までとなります。 'Cost' によるエッジの重みでは、エッジの長さが指定されます。	'Cost'
'incloseness' 'outcloseness'	有向
'betweenness'	無向または有向	中心性タイプ 'betweenness' は、各グラフ ノードがグラフ内の 2 つのノード間の最短経路上に現れる頻度を測定します。2 つのグラフ ノード s と t の間には複数の最短経路が存在する可能性があるため、ノード u の中心性は次のように表されます。 $$c\left(u\right)={\displaystyle \sum _{s,t\ne u}\frac{n_{st}\left(u\right)}{N_{st}}}.$$ $$n_{st}\left(u\right)$$ はノード u を通過する s から t までの最短経路の数、$$N_{st}$$ は s から t までの最短経路の合計数です。 グラフが無向の場合、s から t までの経路と、t から s までの経路は 1 経路としてのみカウントされます (式を 2 で除算)。 'Cost' によるエッジの重みではエッジの長さが指定され、ノード s とノード t 間の最短経路を決めるのに役立ちます。	'Cost'
'pagerank'	無向または有向	中心性タイプ 'pagerank' は、ネットワークのランダム ウォークの結果です。グラフ内の各ノードでは、現在のノードに続くノード (無向の場合は隣接ノード) のセットから、'FollowProbability' の確率で次のノードが選択されます。それ以外の場合、すなわちノードに後続ノードがない場合、次のノードはすべてのノードから選択されます。中心性のスコアは、ランダム ウォーク中に各ノードで費やされた平均時間です。 ノードが自己ループをもつ場合、アルゴリズムは自己ループを通過する可能性があります。このため、自己ループが連結しているノードの pagerank 中心性のスコアは高くなります。 同じ 2 つのノード間に複数のエッジが存在する多重グラフでは、複数のエッジをもつノードが選択される可能性が高くなります。 'Importance' によるエッジの重みは、アルゴリズムが後続ノードを選択する方法に影響します。重要度の高いノードほど、選択される可能性が高くなります。	'Importance' 'FollowProbability' 'Tolerance' 'MaxIterations'
'eigenvector'	無向	中心性タイプ 'eigenvector' では、グラフの隣接行列の最大固有値に対応する固有ベクトルを使用します。スコアは、すべての中心性スコアの合計が 1 になるよう正規化されます。 連結されていないコンポーネントが複数ある場合、アルゴリズムは各コンポーネントについて eigenvector 中心性を個別に計算し、そのコンポーネント内にあるグラフ ノードの割合に従ってスコアをスケーリングします。 連結されていないノードの中心性スコアは 1/numnodes(G) です。 重み付きの隣接行列を計算で使用するには、'Importance' によるエッジの重みを指定します。	'Importance' 'Tolerance' 'MaxIterations'
'hubs' 'authorities'	有向	'hubs' および 'authorities' の各中心性スコアは、2 つの中心性測定が再帰的にリンクされたものです。ノードの hubs スコアは、その後続ノードすべての authorities スコアを合計したものです。同様に authorities スコアは、その先行ノードすべての hubs スコアを合計したものです。すべての hubs スコアの合計は 1 で、またすべての authorities スコアの合計は 1 です。 これらのスコアは、隣接行列の最大特異値に対応する左 (ハブ) および右 (オーソリティ) の特異ベクトルとして解釈できます。 連結されていないノードの中心性スコアは 1/numnodes(G) です。 スコアの単純な合計ではなく、重み付きの合計を使用するにはすべての後続ノードのスコアまたは先行ノードの、'Importance' によるエッジの重みを指定します。これは、重み付き隣接行列の特異ベクトルを使用することと等価です。 連結されていない要素 (弱連結の意味で) が複数ある場合、アルゴリズムは各要素について hubs スコアと authorities スコアを個別に計算します。次に、スコアの合計が 1 のままになるように、その要素内にあるグラフ ノードの割合に従って、スコアが再スケーリングされます。	'Importance' 'Tolerance' 'MaxIterations'

メモ

関数 centrality では、すべてのエッジの重みが 1 に等しいと仮定します。これを変更するには、'Cost' または 'Importance' の名前と値のペアを用いて、使用するエッジの重みを指定します。

例: centrality(G,'degree')

例: centrality(G,'hubs','Tolerance',tol)

名前と値の引数

引数のオプションのペアを Name1=Value1,...,NameN=ValueN として指定します。ここで Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後になければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、コンマを使用してそれぞれの名前と値を区切り、Name を引用符で囲みます。

例: C = centrality(G,'closeness','Cost',edgeCosts) は、グラフ内の各エッジを通過するコスト (重み) として edgeCosts を使用して、近接中心性を計算します。

Cost — エッジ通過のコスト

ベクトル

エッジ通過のコスト。'Cost' とエッジの重みのベクトルで構成されるコンマ区切りのペアとして指定します。i 番目のエッジの重みは、エッジ findedge(G,i) を通過することに関連付けられたコストを指定します。

• 'closeness'、'outcloseness'、および 'incloseness' の中心性タイプについては、エッジのコストは非負でなければなりません。

• 'betweenness' の中心性タイプについては、エッジのコストは正でなければなりません。

連結が短く、速く、あるいは低コストであるほど、'Cost' のエッジの重みは小さくなります。'Cost' によるエッジの重みの例をいくつか示します。

• 経路の長さ

• 移動時間

• チケットのコスト

メモ

'Cost' は、'closeness'、'outcloseness'、'incloseness' および 'betweenness' の中心性タイプにのみ適用されます。

例: centrality(G,'closeness','Cost',c)

FollowProbability — 後続ノードを選択する確率

0.85 (既定値) | 0 ～ 1 のスカラー

後続ノードを選択する確率。'FollowProbability' と、0 ～ 1 のスカラーで構成されるコンマ区切りのペアとして指定します。継承の確率は、通過過程で pagerank アルゴリズムによって選択される次のノードが、すべてのノードからランダムに選択されるのではなく、現在のノードの後続ノード中から選択される確率です。Web サイトの場合、この確率は、別の Web ページをランダムに閲覧するのではなく、現在の Web ページ内にあるリンクをクリックすることと一致します。

メモ

'FollowProbability' は、中心性タイプ 'pagerank' にのみ適用されます。

例: centrality(G,'pagerank','FollowProbability',0.5)

Importance — エッジの重要度

ベクトル

エッジの重要度。'Importance' と非負のエッジ重みのベクトルで構成されるコンマ区切りのペアとして指定します。i 番目のエッジの重みは、エッジ findedge(G,i) の重要度を指定します。エッジの重みをゼロにすると、グラフからそのエッジを削除することと等しくなります。

2 つのノード間に複数のエッジがある多重グラフでは、centrality は複数のエッジをまとめて追加し、それらを重みを組み合わせた 1 つのエッジとして扱います。

連結が強くなるほど、'Importance' によるエッジの重みは大きくなります。'Importance' によるエッジの重みの例をいくつか示します。

• 1 日あたりの旅行者数

• あるリンクのクリック数

• 新聞の合計発行部数

メモ

'Importance' は、'degree'、'outdegree'、'indegree'、'pagerank'、'eigenvector'、'hubs' および 'authorities' の中心性タイプのみに適用されます。

例: centrality(G,'degree','Importance',x)

MaxIterations — 最大反復回数

100 (既定値) | スカラー

最大反復回数。'MaxIterations' とスカラーで構成されるコンマ区切りのペアとして指定します。centrality アルゴリズムは、許容誤差に一致するか、最大反復回数に達するまで (いずれか先に発生した時点まで) 実行されます。

メモ

'MaxIterations' は、'pagerank'、'eigenvector'、'hubs' および 'authorities' の中心性タイプにのみ適用されます。

例: centrality(G,'pagerank','MaxIterations',250)

Tolerance — 反復ソルバーの停止条件

1e-4 (既定値) | スカラー

反復ソルバーの停止条件。'Tolerance' とスカラーで構成されるコンマ区切りのペアとして指定します。centrality アルゴリズムは、許容誤差に一致するか、最大反復回数に達するまで (いずれか先に発生した時点まで) 実行されます。

メモ

'Tolerance' は、'pagerank'、'eigenvector'、'hubs' および 'authorities' の中心性タイプにのみ適用されます。

例: centrality(G,'pagerank','Tolerance',1e-5)

出力引数

C — ノードの中心性スコア

列ベクトル

ノードの中心性スコア。列ベクトルとして返されます。C(i) はノード i の中心性スコアです。ノードの中心性スコアの解釈は、選択した中心性計算のタイプによって異なります。ノードの中心性が高いほど、その中心性スコアは高くなります。

バージョン履歴

R2016a で導入

参考

digraph | graph

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい