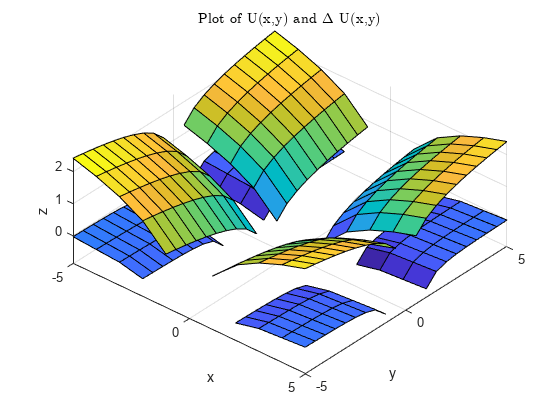
del2

離散ラプラシアン

構文

L = del2(U)

L = del2(U,h)

L = del2(U,hx,hy,...,hN)

説明

L = del2(U) は、すべての点に既定の間隔 h = 1 を使用して U に適用されるラプラス微分演算子の離散近似を返します。

L = del2(U,h) は、U のすべての次元で等しいスカラーの点の間隔 h を指定します。

L = del2(U,hx,hy,...,hN) は、U の各次元における点の間隔 hx,hy,...,hN を指定します。スカラーまたは座標のベクトルとして間隔入力を指定します。間隔入力の数は、U の次元の数と等しくなければなりません。

• 1 番目の間隔の値 hx は、点の x の間隔 (スカラー) または x 座標 (ベクトル) を指定します。ベクトルの場合、その長さは size(U,2) に等しくなければなりません。

• 2 番目の間隔の値 hy は、点の y の間隔 (スカラー) または y 座標 (ベクトル) を指定します。ベクトルの場合、その長さは size(U,1) に等しくなければなりません。

• その他すべての間隔の値は、U の対応する次元における点の間隔 (スカラー) または座標 (ベクトル) を指定します。n > 2 で n 番目の間隔入力がベクトルの場合、その長さは size(U,n) に等しくなければなりません。

例

ベクトルの 2 次導関数

位置データのベクトルから物体の加速度を計算します。

位置データのベクトルを作成します。

p = [1 3 6 10 16 18 29];

物体の加速度を求めるには、del2 を使用して p の 2 階数値微分を計算します。データ点間に既定の間隔 h = 1 を使用します。

L = 4*del2(p)

L = 1×7

     1     1     1     2    -4     9    22

L の各値は、その時点の瞬間加速度の近似です。

余弦ベクトルの 2 次導関数

余弦ベクトルの離散 1 次元ラプラシアンを計算します。

関数の領域を定義します。

x = linspace(-2*pi,2*pi);

これにより、範囲 $$-2\pi \le x\le 2\pi$$ に 100 の点が等間隔で生成されます。

この領域で余弦値のベクトルを作成します。

U = cos(x);

del2 を使用して U のラプラシアンを計算します。領域ベクトル x を使用して、U の各点の 1 次元座標を定義します。

L = 4*del2(U,x);

解析的に、この関数のラプラシアンは $$\Delta U=-\cos (x)$$ と等しくなります。

結果をプロットします。

plot(x,U,x,L)
legend('U(x)','L(x)','Location','Best')

U と L のグラフは、ラプラシアンの解析的結果と一致します。

多変量関数のラプラシアン

多変量関数の離散ラプラシアンを計算およびプロットします。

関数の x および y 領域を定義します。

[x,y] = meshgrid(-5:0.25:5,-5:0.25:5);

この領域で関数 $$U(x,y)=\frac{1}{3}(x^4+y^4)$$ を定義します。

U = 1/3.*(x.^4+y.^4);

del2 を使用してこの関数のラプラシアンを計算します。U の点の間隔はすべての方向で等しいため、単一の間隔入力 h を指定できます。

h = 0.25;
L = 4*del2(U,h);

解析的に、この関数のラプラシアンは $$\Delta U(x,y)=4x^2+4y^2$$ と等しくなります。

離散ラプラシアン L をプロットします。

figure
surf(x,y,L)
grid on
title('Plot of $\Delta U(x,y) = 4x^2+4y^2$','Interpreter','latex')
xlabel('x')
ylabel('y')
zlabel('z')
view(35,14)

L のグラフは、ラプラシアンの解析的結果と一致します。

自然対数関数のラプラシアン

自然対数関数の離散ラプラシアンを計算します。

実数のグリッドで関数の x および y 領域を定義します。

[x,y] = meshgrid(-5:5,-5:0.5:5);

この領域で関数 $$U(x,y)=\frac{1}{2}\log \left(x^{2}y\right)$$ を定義します。

U = 0.5*log(x.^2.*y);

引数 y が負の場合、対数は複素数値になります。

del2 を使用してこの関数の離散ラプラシアンを計算します。各方向のグリッド点の間隔を指定します。

hx = 1; 
hy = 0.5;
L = 4*del2(U,hx,hy);

解析的に、ラプラシアンは $$\Delta U(x,y)=-(1/x^2+1/2y^2)$$ と等しくなります。この関数は、直線 $$x=0$$ または $$y=0$$ 上では定義されません。

U と L の実数部を同じグラフにプロットします。

figure
surf(x,y,real(L))
hold on
surf(x,y,real(U))
grid on
title('Plot of U(x,y) and $\Delta$ U(x,y)','Interpreter','latex')
xlabel('x')
ylabel('y')
zlabel('z')
view(41,58)

上表面が U で、下表面が L です。

入力引数

U — 入力配列

ベクトル | 行列 | 多次元配列

入力配列。ベクトル、行列または多次元配列として指定します。

データ型: single | double
複素数のサポート: あり

h — すべての次元の間隔

1 (既定値) | スカラー

すべての次元の間隔。1 (既定値) またはスカラーとして指定します。

データ型: single | double
複素数のサポート: あり

hx,hy,...,hN — 各次元の間隔 (個別の引数)

スカラー | ベクトル

各次元の間隔。個別のスカラーの引数 (等間隔の場合) またはベクトルの引数 (非等間隔の場合) として指定します。間隔入力の数は、U の次元の数と等しくなければなりません。各間隔入力は、U の 1 つの次元における点の間隔を定義します。

• 1 番目の間隔の値 hx は、点の x の間隔 (スカラー) または x 座標 (ベクトル) を指定します。ベクトルの場合、その長さは size(U,2) に等しくなければなりません。

• 2 番目の間隔の値 hy は、点の y の間隔 (スカラー) または y 座標 (ベクトル) を指定します。ベクトルの場合、その長さは size(U,1) に等しくなければなりません。

• その他すべての間隔の値は、U の対応する次元における点の間隔 (スカラー) または座標 (ベクトル) を指定します。n > 2 で n 番目の間隔入力がベクトルの場合、その長さは size(U,n) に等しくなければなりません。

データ型: single | double
複素数のサポート: あり

出力引数

L — 離散ラプラシアン近似

ベクトル | 行列 | 多次元配列

離散ラプラシアン近似。ベクトル、行列または多次元配列として返されます。L は入力 U と同じサイズです。

詳細

ラプラス微分演算子

MATLAB^® の del2 で使用されるラプラス演算子の定義は、U のデータの次元に応じて異なります。

• U が、線の点で計算される関数 U(x) を表すベクトルである場合、del2(U) は、以下の有限差分近似になります。

  $$L=\frac{\Delta U}{4}=\frac{1}{4}\frac{{\partial }^{2}U}{\partial x^2}.$$

• 行列 U が、正方格子の点で計算される関数 U(x,y) である場合、del2(U) は、以下の有限差分近似になります。

  $$L=\frac{\Delta U}{4}=\frac{1}{4}\left(\frac{{\partial }^{2}U}{\partial x^2}+\frac{{\partial }^{2}U}{\partial y^2}\right).$$

• 変数が 3 つ以上の関数 U(x,y,z,...) の場合、離散ラプラシアン del2(U) は各次元で 2 次導関数を計算します。

  $$L=\frac{\Delta U}{2N}=\frac{1}{2N}\left(\frac{{\partial }^{2}U}{\partial x^2}+\frac{{\partial }^{2}U}{\partial y^2}+\frac{{\partial }^{2}U}{\partial z^2}+\mathrm{...}\right),$$

  ここで、N は U の次元数であり、$$N\ge 2$$ です。

アルゴリズム

入力 U が行列の場合、L の内部点は、U の点と、その 4 つの近傍の平均との差分を取得して検出されます。

$$L_{ij}=\left[\frac{\left(u_{i+1,j}+u_{i-1,j}+u_{i,j+1}+u_{i,j-1}\right)}{4}-u_{i,j}\right].$$

次に、del2 は内部から 2 階差分を線形に外挿することで、L のエッジの値を計算します。この式は、多次元 U に対して拡張されます。

拡張機能

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。

GPU コード生成
GPU Coder™ を使用して NVIDIA® GPU のための CUDA® コードを生成します。

スレッドベースの環境

MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

del2 関数は、GPU 配列を完全にサポートします。GPU 上で関数を実行するには、入力データを gpuArray (Parallel Computing Toolbox) として指定します。詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

分散配列

Parallel Computing Toolbox™ を使用して、クラスターの結合メモリ上で大きなアレイを分割します。

この関数は分散配列を完全にサポートしています。詳細については、分散配列を使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2006a より前に導入

参考

diff | gradient