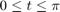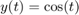ddensd

中立型の遅延微分方程式 (DDE) を解く

ページ内をすべて折りたたむ

構文

sol = ddensd(ddefun,dely,delyp,history,tspan)
sol = ddensd(ddefun,dely,delyp,history,tspan,options)

説明

sol = ddensd(ddefun,dely,delyp,history,tspan) は、次の形式をもつ中立型の連立遅延微分方程式を積分します。

y '(t) = f(t, y(t), y(dy1),..., y(dyp), y '(dyp1),..., y '(dypq))(1)
ここで

  • t は、時間を表す独立変数です。

  • dyi は、解の遅延 p 個のいずれかです。

  • dypi は、導関数の遅延 q 個のいずれかです。

例

sol = ddensd(ddefun,dely,delyp,history,tspan,options) は、既定の積分パラメーターを、関数 ddeset で作成された構造体 options で指定されたものに置き換えます。

例

すべて折りたたむ

スクリプトを開く

Paul により提示された次の中立型 DDE を $0 \le t \le \pi$ について解きます。

$$y'(t) = 1 + y(t) - 2y(t/2)^2 - y'(t-\pi)$$

解の履歴は $t \le 0$ で $y(t) = \cos(t)$ です。

新しいプログラム ファイルをエディターで作成します。このファイルには、1 つのメイン関数と 4 つのローカル関数が記述されます。

1 次 DDE を ddefun というローカル関数として定義します。

function yp = ddefun(t,y,ydel,ypdel) 
    yp = 1 + y - 2*ydel^2 - ypdel;
end

解の遅延を dely というローカル関数として定義します。

function dy = dely(t,y) 
    dy = t/2;
end

導関数の遅延を delyp というローカル関数として定義します。

function dyp = delyp(t,y) 
    dyp = t-pi;
end

解の履歴を history というローカル関数として定義します。

function y = history(t)
    y = cos(t);
end

積分区間を定義し、ddensd を使用して DDE を解きます。このコードをメイン関数に追加します。

tspan = [0 pi];
sol = ddensd(@ddefun,@dely,@delyp,@history,tspan);

$0$ から $\pi$ までにある等間隔の 100 点で解を計算します。このコードをメイン関数に追加します。

tn = linspace(0,pi);
yn = deval(sol,tn);

結果をプロットします。このコードをメイン関数に追加します。

plot(tn,yn);
xlim([0 pi]);
ylim([-1.2 1.2]);
xlabel('time t');
ylabel('solution y');

プログラム全体を実行し、解を計算してプロットを表示します。ファイル ddex4.m にこの例のコードがすべて含まれています。エディターでコードを表示するには、コマンド ラインで edit ddex4 と入力します。

入力引数

すべて折りたたむ

導関数を、yp = ddefun(t,y,ydel,ypdel) をその構文とする関数ハンドルとして指定します。次の表は、ddefun の引数をまとめています。

ddefun 引数説明
t時間 t の現在の値を表すスカラー値。
y 式 1 での y(t) を表すベクトル。このベクトルのサイズは、n 行 1 列であり、ここで n は、解を求めたいシステムにおける方程式の数です。
ydel列 ydel(:,i) が y(dyi) を表す行列。この行列のサイズは n 行 p 列であり、ここで n は、解を求めたいシステムにおける方程式の数であり、p は、式 1 における y(dy) 項の数です。
ypdel列 ypdel(:,j) が y '(dypj) を表す行列。この行列のサイズは n 行 q 列であり、ここで n は、解を求めたいシステムにおける方程式の数であり、q は、式 1 における y '(dyp) 項の数です。
ypddefun で返される結果。要素が 式 1 の右辺を表す n 行 1 列のベクトルです。

解の遅延。式 1において dy1,..., dyp を返す関数ハンドルとして指定します。あるいは、ベクトルの形式で定数の遅れを渡すこともできます。

dely を関数ハンドルとして指定する場合、構文は dy = dely(t,y) でなければなりません。次の表は、この関数の引数をまとめています。

dely 引数説明
t時間 t の現在の値を表すスカラー値。
y式 1 での y(t) を表すベクトル。このベクトルのサイズは、n 行 1 列であり、ここで n は、解を求めたいシステムにおける方程式の数です。
dy関数 dely によって返されるベクトルであり、その値は、式 1 における解の遅延 dyi です。このベクトルのサイズは、p 行 1 列であり、ここで p は、方程式における解の遅延の数です。各要素は、t 以下でなければなりません。

形式 dyi = t – τi をもつ定数の解の遅延を指定する場合、dely は、dely(i) = τi となるベクトルでなければなりません。このベクトルの各値は、ゼロ以上でなければなりません。

dy が問題にない場合、dely を [] に設定します。

データ型: function_handle | single | double

導関数の遅延。式 1の dyp1,..., dypq を返す関数ハンドルとして指定します。あるいは、ベクトルの形式で定数の遅れを渡すこともできます。

delyp が関数ハンドルである場合、その構文は dyp = delyp(t,y) でなければなりません。次の表は、この関数の引数をまとめています。

delyp 引数説明
t時間 t の現在の値を表すスカラー値。
y式 1 での y(t) を表すベクトル。このベクトルのサイズは、n 行 1 列であり、ここで n は、解を求めたいシステムにおける方程式の数です。
dyp関数 delyp によって返されるベクトルであり、その値は、式 1 における導関数の遅延 dypj です。このベクトルのサイズは、q 行 1 列でなければなりません。ここで q は、方程式における解の遅延 dypj の数です。dyp の各要素は、t 未満でなければなりません。この制限には、例外が 1 つあります。初期値 DDE を解く場合、dyp の値は、t = t0 において t に等しくなります。詳細については、初期値中立遅延微分方程式を参照してください。

形式 dypj = t – τj をもつ定数の導関数の遅延を指定する場合、delyp は、delyp(j) = τj となるベクトルでなければなりません。このベクトルの各値は、ゼロより大きくなければなりません。この制限への例外は、中立型の DDE について初期値問題を解く場合に発生します。このような場合、delyp の値は、t = t0 において 0 に等しくなります。詳細については、初期値中立遅延微分方程式を参照してください。

dyp が問題にない場合、delyp を [] に設定します。

データ型: function_handle | single | double

解の履歴を、関数ハンドル、列ベクトル、sol 構造体 (前の積分から) または cell 配列として指定します。これは、t ≤ t0 における解です。

  • 履歴が時間と共に変化する場合、構文を y = history(t) とする関数ハンドルとして解の履歴を指定します。この関数は、解 y(t) を t <= t0 について近似する n 行 1 列のベクトルを返します。このベクトルの長さは、n であり、これは、解を求めたいシステムにおける方程式の数です。

  • y(t) が定数である場合、history を定数値の n 行 1 列のベクトルとして指定できます。

  • 前の積分を t0 まで継続するために ddensd を呼び出す場合、前の積分から出力 sol として履歴を指定できます。

  • 初期値 DDE を解く場合、cell 配列 {y0, yp0} として履歴を指定します。最初の要素 y0 は、初期値 y(t0) の列ベクトルです。2 番目の要素 yp0 は、要素が初期導関数 y '(t0) である列ベクトルです。これらのベクトルには、矛盾がないようにしなければなりません。すなわち、いずれもが t0 において式 1 を満たします。詳細については、初期値中立遅延微分方程式を参照してください。

データ型: function_handle | single | double | struct | cell

積分区間を、ベクトル [t0 tf] として指定します。最初の要素 t0 は、t の初期値です。2 番目の要素 tf は、t の最終値です。t0 の値は、 tf 未満でなければなりません。

データ型: single | double

オプションの積分パラメーター。関数 ddeset が作成して返す構造体として指定します。一般に利用されるプロパティは、'RelTol'、'AbsTol' および 'Events' です。options の指定の詳細については、ddeset のリファレンス ページを参照してください。

出力引数

すべて折りたたむ

以下のフィールドを含む構造体として返される解。

sol.xddensd で選択されたメッシュ
sol.yメッシュ点での y(t) への近似。
sol.ypメッシュ点での y '(t) への近似。
sol.solverソルバー 'ddensd' を識別する文字ベクトル。

特定の点での解を計算するため、sol を関数 deval に渡すことができます。たとえば、y = deval(sol, 0.5*(sol.x(1) + sol.x(end))) は、積分区間の中点で解を計算します。

詳細

すべて折りたたむ

アルゴリズム

このソルバーで使用されるアルゴリズムの詳細については、Shampine [2]を参照してください。

参照

[1] Paul, C.A.H. “A Test Set of Functional Differential Equations.” Numerical Analysis Reports. No. 243. Manchester, UK: Math Department, University of Manchester, 1994.

[2] Shampine, L.F. “Dissipative Approximations to Neutral DDEs.” Applied Mathematics & Computation. Vol. 203, Number 2, 2008, pp. 641–648.

バージョン履歴

R2012b で導入

参考

| | |

トピック