PageRank アルゴリズムを使用した Web サイトのランク付け

ライブスクリプトを開く

この例では、PageRank アルゴリズムを使用して Web サイトの集まりにランクを付ける方法を示します。PageRank アルゴリズムは元々検索エンジンの結果をランク付けするよう設計されたものですが、より広範の多くの異なるタイプのグラフでノードに対して適用することもできます。PageRank のスコアは、各グラフノードが他のノードとどのように結合しているかに基づき、その相対的な重要性を示します。

理論的には、PageRank のスコアは、誰かが各 Web サイトのリンクをランダムにクリックして特定のページにたどり着く極限確率です。したがって、高いスコアのページはネットワーク内で密接に結合しており、検出されやすく、ランダムに Web サーフィンをしている人がそのページを訪れる可能性が高くなります。

アルゴリズムの説明

PageRank アルゴリズムの各ステップで、各ページのスコアは次のように更新されます。

r = (1-P)/n + P*(A'*(r./d) + s/n);

r は PageRank スコアのベクトルです。
P はスカラー値の減衰係数 (通常 0.85) です。これは、ランダムなサーファーが別のページにランダムに移動せず、現在のページ内にあるリンクをクリックする確率です。
A' はグラフの隣接行列の転置です。
d はグラフ内の各ノードの出次数が含まれるベクトルです。出力エッジをもたないノードについては、d は 1 に設定されます。
n はグラフ内のノード数のスカラーです。
s はリンクをもたないページに対する、PageRank スコアのスカラーの合計です。

つまり、各ページのランクは、そのページにリンクするページのランクに大きく左右されます。項 A'*(r./d) は、グラフ内の各ノードにリンクするソースノードのスコアを抽出します。また、スコアはこれらソースノードのアウトバウンドリンクの合計数によって正規化されます。これにより、PageRank スコアの合計は必ず 1 になります。たとえば、ノード 2 がノード 1、3 および 4 にリンクしている場合、アルゴリズムの各反復に際し、その PageRank スコアの 1/3 がこれらの各ノードに転移します。

グラフ内の各ノードがどのようにその PageRank スコアを他のノードに与えるかを示すグラフを作成します。

s = {'a' 'a' 'a' 'b' 'b' 'c' 'd' 'd' 'd'};
t = {'b' 'c' 'd' 'd' 'a' 'b' 'c' 'a' 'b'};
G = digraph(s,t);
labels = {'a/3' 'a/3' 'a/3' 'b/2' 'b/2' 'c' 'd/3' 'd/3' 'd/3'};
p = plot(G,'Layout','layered','EdgeLabel',labels);
highlight(p,[1 1 1],[2 3 4],'EdgeColor','g')
highlight(p,[2 2],[1 4],'EdgeColor','r')
highlight(p,3,2,'EdgeColor','m')
title('PageRank Score Transfer Between Nodes')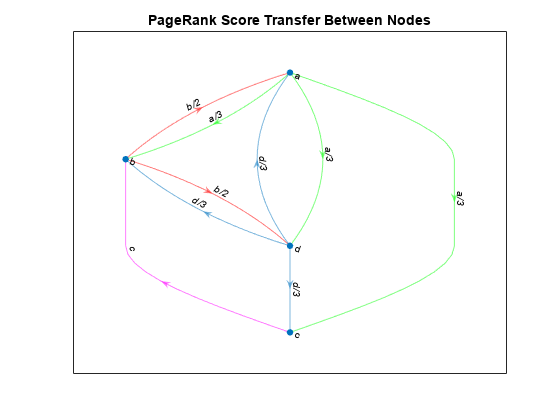

関数 centrality には、PageRank スコアを計算するオプションが含まれています。

6 つのノードでの PageRank

架空の Web サイトを表す 6 つのノードが含まれる有向グラフを作成し、プロットします。

s = [1 1 2 2 3 3 3 4 5];
t = [2 5 3 4 4 5 6 1 1];
names = {'http://www.example.com/alpha', 'http://www.example.com/beta', ...
         'http://www.example.com/gamma', 'http://www.example.com/delta', ...
         'http://www.example.com/epsilon', 'http://www.example.com/zeta'};
G = digraph(s,t,[],names)

G = 
  digraph with properties:

    Edges: [9x1 table]
    Nodes: [6x1 table]

plot(G,'Layout','layered', ...
    'NodeLabel',{'alpha','beta','gamma','delta','epsilon','zeta'})

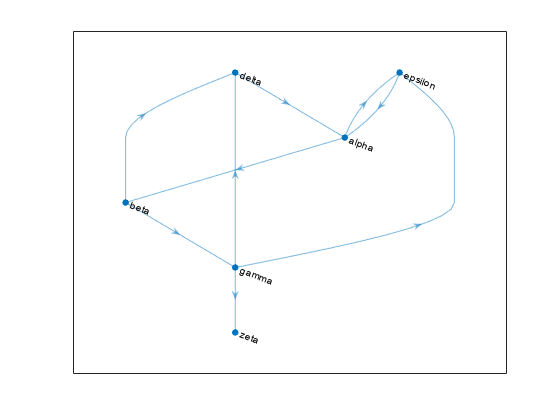
このグラフの PageRank の中心性スコアを計算します。フォローの確率 (また減衰係数として知られている) には 0.85 を使用します。

pr = centrality(G,'pagerank','FollowProbability',0.85)

各ページの PageRank スコアと次数情報を表示します。

G.Nodes.PageRank = pr;
G.Nodes.InDegree = indegree(G);
G.Nodes.OutDegree = outdegree(G);
G.Nodes

ans=6×4 table
                   Name                   PageRank    InDegree    OutDegree
    __________________________________    ________    ________    _________

    {'http://www.example.com/alpha'  }    0.32098        2            2    
    {'http://www.example.com/beta'   }    0.17057        1            2    
    {'http://www.example.com/gamma'  }    0.10657        1            3    
    {'http://www.example.com/delta'  }    0.13678        2            1    
    {'http://www.example.com/epsilon'}    0.20078        2            1    
    {'http://www.example.com/zeta'   }    0.06432        1            0

結果には、スコアはページリンクの "数" だけではなく、"質" にも左右されることが示されています。alpha と gamma の Web サイトはどちらも合計次数が 4 ですが、alpha は同じくランクの高い epsilon と beta の両方にリンクしています。gamma へとリンクしているのは 1 つのページ beta のみで、これはリストの中間に位置しています。したがって、アルゴリズムによって alpha のスコアは gamma よりも高くなります。

mathworks.com 上の Web サイトの PageRank

mathworks100.mat のデータを読み込み、隣接行列 A を表示します。このデータは 2015 年に自動のページクローラーを使用して生成されたものです。ページクローラーは https://www.mathworks.com から始めて、100 ページにわたる一意の Web ページの結合について情報が隣接行列に格納されるまで、後続する Web ページへのリンクをたどっていきました。

load mathworks100.mat 
spy(A)

U に含まれている URL をノード名として使用し、スパース隣接行列 A を用いて有向グラフを作成します。

G = digraph(A,U)

G = 
  digraph with properties:

    Edges: [632x1 table]
    Nodes: [100x1 table]

フォースレイアウトを使用してグラフをプロットします。

plot(G,'NodeLabel',{},'NodeColor',[0.93 0.78 0],'Layout','force');
title('Websites linked to https://www.mathworks.com')

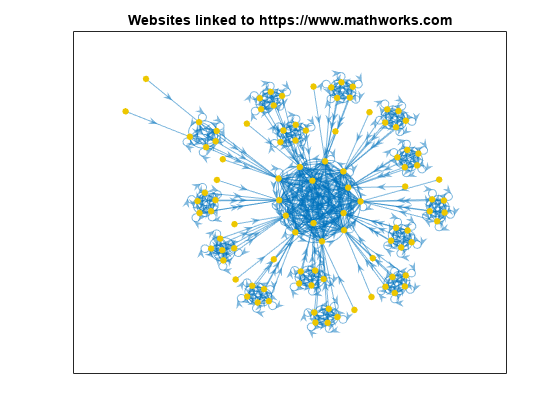
200 回の反復と 0.85 の減衰係数を使用して、グラフ G の PageRank スコアを計算します。スコアと次数情報をグラフのノードテーブルに追加します。

pr = centrality(G,'pagerank','MaxIterations',200,'FollowProbability',0.85);
G.Nodes.PageRank = pr;
G.Nodes.InDegree = indegree(G);
G.Nodes.OutDegree = outdegree(G);

スコアの結果の上位 25 を表示します。

G.Nodes(1:25,:)

ans=25×4 table
                                         Name                                         PageRank    InDegree    OutDegree
    ______________________________________________________________________________    ________    ________    _________

    {'https://www.mathworks.com'                                                 }    0.044342       20          14    
    {'https://ch.mathworks.com'                                                  }    0.043085       20          14    
    {'https://cn.mathworks.com'                                                  }    0.043085       20          14    
    {'https://jp.mathworks.com'                                                  }    0.043085       20          14    
    {'https://kr.mathworks.com'                                                  }    0.043085       20          14    
    {'https://uk.mathworks.com'                                                  }    0.043085       20          14    
    {'https://au.mathworks.com'                                                  }    0.043085       20          14    
    {'https://de.mathworks.com'                                                  }    0.043085       20          14    
    {'https://es.mathworks.com'                                                  }    0.043085       20          14    
    {'https://fr.mathworks.com'                                                  }    0.043085       20          14    
    {'https://in.mathworks.com'                                                  }    0.043085       20          14    
    {'https://it.mathworks.com'                                                  }    0.043085       20          14    
    {'https://nl.mathworks.com'                                                  }    0.043085       20          14    
    {'https://se.mathworks.com'                                                  }    0.043085       20          14    
    {'https://www.mathworks.com/index.html%3Fnocookie%3Dtrue'                    }      0.0015        0           1    
    {'https://www.mathworks.com/company/aboutus/policies_statements/patents.html'}    0.007714        6           6    
      ⋮

スコアが 0.005 を超えるすべてのノードが含まれる部分グラフを抽出し、プロットします。PageRank スコアに基づきグラフノードの色付けを行います。

H = subgraph(G,find(G.Nodes.PageRank > 0.005));
plot(H,'NodeLabel',{},'NodeCData',H.Nodes.PageRank,'Layout','force');
title('Websites linked to https://www.mathworks.com')
colorbar

上位の Web サイトの PageRank スコアはどれもあまり変わらず、ランダムな Web サーファーが各ページを訪れる可能性は約 4.5% です。密接に結合したページから成るこの小さなグループは、プロットの中心でクリークを形成しています。この中央のクリークにはいくつかのさらに小さなクリークが結合しており、それらはそれ自体の中で密接に結合しています。

参照

Moler, C. Experiments with MATLAB.Chapter 7: Google PageRank.MathWorks, Inc., 2011.

参考

digraph | graph | centrality