米国の人口を予測

この例では、多項式を使用したデータの外挿は、適度であっても、危険で信頼性が低いことを示します。

この例の予測は、MATLAB® が作成されるより前に行われたものです。1977 年に Prentice-Hall によって公表され、Forsythe、Malcolm、および Moler らの Computer Methods for Mathematical Computations 内の演習として始まりました。

現在では、MATLAB によって、パラメーターを変更して結果を見ることは大変容易に行えますが、根本的な数学的法則は変わりません。

1910 年から 2000 年の米国の人口調査データを使用して 2 つのベクトルを作成してプロットします。

% Time interval
t = (1910:10:2000)';

% Population
p = [91.972 105.711 123.203 131.669 150.697...
    179.323 203.212 226.505 249.633 281.422]';

% Plot
plot(t,p,'bo');
axis([1910 2020 0 400]);
title('Population of the US 1910-2000');
ylabel('Millions');

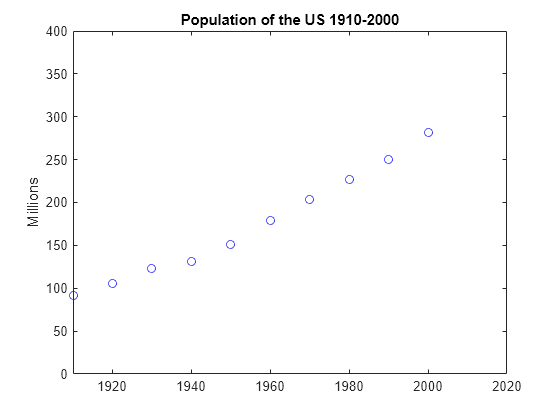
Figure contains an axes object. The axes object with title Population of the US 1910-2000, ylabel Millions contains a line object which displays its values using only markers.

2010 年には人口はどうなると推定しますか?

t の多項式でデータに当てはめ、これを使用して t = 2010 に人口値を外挿します。多項式の係数を取得するため、要素がスケーリングした時間 A(i,j) = s(i)^(n-j) の乗数として 11 行 11 列のヴァンデルモンド行列をもつ線形連立方程式を解きます。

n = length(t);
s = (t-1950)/50;
A = zeros(n);
A(:,end) = 1;
for j = n-1:-1:1
   A(:,j) = s .* A(:,j+1);
end

データ p に当てはめる次数 d の多項式である係数 c を取得するために、ヴァンデルモンド行列の最後の d+1 列を含む線形連立方程式を解きます。

A(:,n-d:n)*c ~= p

d < 10 の場合、未知数より方程式の数が多くなり、最小二乗解は適切です。
d == 10 の場合、その方程式の厳密な解を求めることができ、多項式は実際にデータを内挿します。

どちらの場合も、バックスラッシュ演算子を使用して方程式を解きます。3 次の近似に対する係数は、次のとおりです。

c = A(:,n-3:n)\p

1910 年から 2010 年の各年で多項式を評価し、結果をプロットします。

v = (1910:2020)';
x = (v-1950)/50;
w = (2010-1950)/50;
y = polyval(c,x);
z = polyval(c,w);

hold on
plot(v,y,'k-');
plot(2010,z,'ks');
text(2010,z+15,num2str(z));
hold off

Figure contains an axes object. The axes object with title Population of the US 1910-2000, ylabel Millions contains 4 objects of type line, text. One or more of the lines displays its values using only markers

3 次と 4 次多項式近似を比較します。外挿の点が大きく異なることに注意してください。

c = A(:,n-4:n)\p;
y = polyval(c,x);
z = polyval(c,w);

hold on
plot(v,y,'k-');
plot(2010,z,'ks');
text(2010,z-15,num2str(z));
hold off

Figure contains an axes object. The axes object with title Population of the US 1910-2000, ylabel Millions contains 7 objects of type line, text. One or more of the lines displays its values using only markers

次数が増加すると、外挿はさらに不安定になります。

cla
plot(t,p,'bo')
hold on
axis([1910 2020 0 400])
colors = hsv(8);
labels = {'data'};
for d = 1:8
   [Q,R] = qr(A(:,n-d:n));
   R = R(1:d+1,:);
   Q = Q(:,1:d+1);
   c = R\(Q'*p);    % Same as c = A(:,n-d:n)\p;
   y = polyval(c,x);
   z = polyval(c,w);
   plot(v,y,'color',colors(d,:));
   plot(2010,z,'s','color',colors(d,:));
   labels{end+1} = ['degree = ' int2str(d)];
   labels{end+1} = '';
end
legend(labels, 'Location', 'NorthWest')
hold off

Figure contains an axes object. The axes object contains 17 objects of type line. One or more of the lines displays its values using only markers These objects represent data, degree = 1, degree = 2, degree = 3, degree = 4, degree = 5, degree = 6, degree = 7, degree = 8.

参考

polyfit