捕食者と被食者の方程式の求解

ライブスクリプトを開く

この例では、ルンゲ・クッタ積分手法の可変ステップサイズを使用して、捕食者/被食者モデルを表す微分方程式を解く方法を示します。ode23 メソッドは、中規模な精度に対して 2 次、3 次の公式の組み合わせを使用し、ode45 メソッドは、高い精度に対して 4 次、5 次の組み合わせを使用します。

Lotka-Volterra の方程式または捕食者と被食者のモデルとして知られる 1 次の常微分方程式の組み合わせについて考えます。

$\begin{array}{l} \frac{dx}{dt} = x - α xy \\ \frac{dy}{dt} = - y + β xy . \end{array}$

変数 $x$ および $y$ は、被捕食者と捕食者のそれぞれの個体群のサイズを表します。2 次のクロス項は、種の間の相互関係を説明します。捕食者が存在しない場合に被捕食者の個体群は増加し、被捕食者が少なくなると捕食者の個体群は減少します。

方程式のコード作成

連立方程式のシミュレーションを実行するために、状態と時間の値を与えて、状態導関数の列ベクトルを返す関数を作成します。2 つの変数 $x$ および $y$ は、MATLAB® でベクトル y の最初の 2 つの値として表すことができます。同様に、導関数はベクトル yp の最初の 2 つの値です。この関数は t および y の値を受け入れて、yp の方程式によって生成された値を返さなければなりません。

yp(1) = (1 - alpha*y(2))*y(1)

yp(2) = (-1 + beta*y(1))*y(2)

この例では、方程式は lotka.m というファイルに含まれています。このファイルでは、 $α = 0.01$ および $β = 0.02$ のパラメーター値を使用します。

type lotka

function yp = lotka(t,y)
%LOTKA  Lotka-Volterra predator-prey model.

%   Copyright 1984-2014 The MathWorks, Inc.

yp = diag([1 - .01*y(2), -1 + .02*y(1)])*y;

連立方程式のシミュレーション

ode オブジェクトを作成して問題と初期条件を定義します。 $x (0) = y (0) = 20$ の初期条件を使用して、最初は捕食者と被捕食者の個体群が等しくなるようにします。ode23 ソルバーを使用するように指定します。その後、solve メソッドを使用して、時間区間 $0 < t < 15$ で連立方程式をシミュレートします。

y0 = [20; 20];   
F = ode(ODEFcn=@lotka,InitialValue=y0,Solver="ode23")

F = 
  ode with properties:

   Problem definition
               ODEFcn: @lotka
          InitialTime: 0
         InitialValue: [2×1 double]
         EquationType: standard

   Solver properties
    AbsoluteTolerance: 1.0000e-06
    RelativeTolerance: 1.0000e-03
               Solver: ode23

  Show all properties

t0 = 0;
tfinal = 15;
S = solve(F,t0,tfinal);
t = S.Time;
y = S.Solution;

結果のプロット

時間に対して結果の個体群をプロットします。

plot(t,y,"-o")
title("Predator/Prey Populations Over Time")
xlabel("t")
ylabel("Population")
legend("Prey","Predators",Location="north")

Figure contains an axes object. The axes object with title Predator/Prey Populations Over Time, xlabel t, ylabel Population contains 2 objects of type line. These objects represent Prey, Predators.

次に、相互に個体群をプロットします。結果の位相面プロットにより、個体群間の巡回的な関係が非常に明らかになります。

plot(y(1,:),y(2,:))
title("Phase Plane Plot")
xlabel("Prey Population")
ylabel("Predator Population")

Figure contains an axes object. The axes object with title Phase Plane Plot, xlabel Prey Population, ylabel Predator Population contains an object of type line.

さまざまなソルバーの結果の比較

2 度目は ode23 ではなく ode45 ソルバーを使用して連立方程式を解きます。ode45 ソルバーでは、各手順において時間がかかりますが、手順もより大きくなります。それにもかかわらず、既定の設定で、ソルバーは連続的な拡張式を利用して、使用した各ステップの期間において 4 つの等間隔な時間点で出力を生成するため、ode45 の出力は滑らかです (solve メソッドの名前と値の引数 Refine を使用して点の数を調整できます。)比較のために両方の解をプロットします。

F.Solver = "ode45";
S2 = solve(F,t0,tfinal);
t2 = S2.Time;
y2 = S2.Solution;

plot(y(1,:),y(2,:),"o",y2(1,:),y2(2,:),".");
title("Phase Plane Plot")
legend("ode23","ode45")

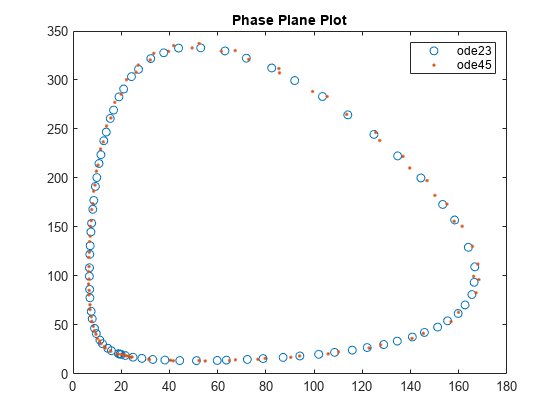
Figure contains an axes object. The axes object with title Phase Plane Plot contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent ode23, ode45.

結果は、異なる数値的手法を使用して微分方程式を解くと、若干異なる解が生成されることを示します。

参考

ode45 | ode23

捕食者と被食者の方程式の求解

方程式のコード作成

連立方程式のシミュレーション

結果のプロット

さまざまなソルバーの結果の比較

参考

トピック