微分方程式

この例では、MATLAB® を使用して、いくつかの異なる種類の微分方程式に対する公式と解法を示します。MATLAB は、広範な微分方程式を解くためのさまざまな数値的アルゴリズムを提供します。

初期値問題
境界値問題
遅延微分方程式
偏微分方程式

開始値問題

vanderpoldemo は、ファンデルポールの方程式を定義する関数です。

$\frac{d^{2} y}{d t^{2}} - μ (1 - y^{2}) \frac{d y}{d t} + y = 0 .$

type vanderpoldemo

function dydt = vanderpoldemo(t,y,Mu)
%VANDERPOLDEMO Defines the van der Pol equation for ODEDEMO.

% Copyright 1984-2014 The MathWorks, Inc.

dydt = [y(2); Mu*(1-y(1)^2)*y(2)-y(1)];

方程式は、2 つの 1 次常微分方程式 (ODE) 系として記述されます。これらの方程式は、パラメーター $μ$ のさまざまな値に対して評価されます。より速く積分を行うには、 $μ$ の値に基づいて適切なソルバーを選択しなければなりません。

$μ = 1$ の場合、MATLAB ODE ソルバーのいずれでもファンデルポールの方程式を効率的に解くことができます。ode45 ソルバーは、そのような例の 1 つです。方程式は、初期条件 $y (0) = 2$ および $\frac{dy}{dt} |_{t = 0} = 0$ を使用して、領域 $[0, 20]$ 内で解かれます。

tspan = [0 20];
y0 = [2; 0];
Mu = 1;
ode = @(t,y) vanderpoldemo(t,y,Mu);
[t,y] = ode45(ode, tspan, y0);

% Plot solution
plot(t,y(:,1))
xlabel('t')
ylabel('solution y')
title('van der Pol Equation, \mu = 1')

Figure contains an axes object. The axes object with title v a n blank d e r blank P o l blank E q u a t i o n , blank mu blank = blank 1 contains an object of type line.

$μ$ がより大きくなると、問題は "スティッフ" になります。このラベルは、通常の手法によって評価されることを拒否する問題のためのものです。代わりに、より速く積分を行うには、特別な数値メソッドが必要になります。関数 ode15s、ode23s、ode23t および ode23tb は、スティッフな問題を効率的に解決します。

$μ = 1000$ のファンデルポールの方程式に対する次の解では、同じ初期条件で ode15s を使用します。解の定期的な移動を確認できるように、時間範囲を $[0, 3000]$ へと大幅に広げる必要があります。

tspan = [0, 3000];
y0 = [2; 0];
Mu = 1000;
ode = @(t,y) vanderpoldemo(t,y,Mu);
[t,y] = ode15s(ode, tspan, y0);

plot(t,y(:,1))
title('van der Pol Equation, \mu = 1000')
axis([0 3000 -3 3])
xlabel('t')
ylabel('solution y')

Figure contains an axes object. The axes object with title v a n blank d e r blank P o l blank E q u a t i o n , blank mu blank = blank 1 0 0 0 contains an object of type line.

境界値問題

bvp4c および bvp5c は、常微分方程式 (ODE) の境界値問題を解きます。

例の関数 twoode は、2 つの 1 次 ODE 系として記述された微分方程式になります。微分方程式は、次のとおりです。

$\frac{d^{2} y}{d t^{2}} + | y | = 0 .$

type twoode

function dydx = twoode(x,y)
%TWOODE  Evaluate the differential equations for TWOBVP.
%
%   See also TWOBC, TWOBVP.

%   Lawrence F. Shampine and Jacek Kierzenka
%   Copyright 1984-2014 The MathWorks, Inc.

dydx = [ y(2); -abs(y(1)) ];

関数 twobc は、この問題に対し $y (0) = 0$ および $y (4) = - 2$ の境界条件をもちます。

type twobc

function res = twobc(ya,yb)
%TWOBC  Evaluate the residual in the boundary conditions for TWOBVP.
%
%   See also TWOODE, TWOBVP.

%   Lawrence F. Shampine and Jacek Kierzenka
%   Copyright 1984-2014 The MathWorks, Inc.

res = [ ya(1); yb(1) + 2 ];

bvp4c を呼び出す前に、メッシュで表すために解の推定値を与えなければなりません。ソルバーは、その後、解の推定値を絞り込むときにメッシュを適応させます。

関数 bvpinit は、ソルバー bvp4c に渡すことができるフォームで初期推定を作成します。[0 1 2 3 4] のメッシュおよび $y (x) = 1$ および $y' (x) = 0$ の定数の推定の場合、bvpinit の呼び出しは以下のようになります。

solinit = bvpinit([0 1 2 3 4],[1; 0]);

この初期推定を使うことで、bvp4c で問題を解くことができます。deval を使用して、いくつかの点で bvp4c によって返される解を評価し、結果の値をプロットします。

sol = bvp4c(@twoode, @twobc, solinit);

xint = linspace(0, 4, 50);
yint = deval(sol, xint);
plot(xint, yint(1,:));
xlabel('x')
ylabel('solution y')
hold on

Figure contains an axes object. The axes object contains an object of type line.

この特定の境界値問題は、正確には 2 つの解をもちます。初期推定を $y (x) = - 1$ および $y' (x) = 0$ に変更することで、他の解を取得できます。

solinit = bvpinit([0 1 2 3 4],[-1; 0]);
sol = bvp4c(@twoode,@twobc,solinit);

xint = linspace(0,4,50);
yint = deval(sol,xint);
plot(xint,yint(1,:));
legend('Solution 1','Solution 2')
hold off

Figure contains an axes object. The axes object contains 2 objects of type line. These objects represent Solution 1, Solution 2.

遅延微分方程式

dde23、ddesd および ddensd は、各種の遅延を使用して遅延微分方程式を解きます。例の ddex1、ddex2、ddex3、ddex4 および ddex5 は、これらのソルバーの使用方法に関するミニチュートリアルです。

ddex1 の例は、微分方程式系を解く方法を示します。

$\begin{array}{l} y_{1}^{'} (t) = y_{1} (t - 1) \\ y_{2}^{'} (t) = y_{1} (t - 1) + y_{2} (t - 0.2) \\ y_{3}^{'} (t) = y_{2} (t) . \end{array}$

これらの方程式を無名関数を使用して表すことができます。

ddex1fun = @(t,y,Z) [Z(1,1); Z(1,1)+Z(2,2); y(2)];

問題の履歴 ( $t \leq 0$ の場合) は一定となります。

$\begin{array}{l} y_{1} (t) = 1 \\ y_{2} (t) = 1 \\ y_{3} (t) = 1 . \end{array}$

履歴を ones のベクトルとして表すことができます。

ddex1hist = ones(3,1);

2 要素ベクトルは、方程式系における遅延を表します。

lags = [1 0.2];

関数、遅延、解の履歴、積分区間 $[0, 5]$ を入力としてソルバーに渡します。ソルバーは、プロットに適している積分区間の全体に渡り、連続的な解を算出します。

sol = dde23(ddex1fun, lags, ddex1hist, [0 5]);

plot(sol.x,sol.y);
title({'An example of Wille and Baker', 'DDE with Constant Delays'});
xlabel('time t');
ylabel('solution y');
legend('y_1','y_2','y_3','Location','NorthWest');

Figure contains an axes object. The axes object with title An example of Wille and Baker DDE with Constant Delays contains 3 objects of type line. These objects represent y_1, y_2, y_3.

偏微分方程式

pdepe は、1 つの空間変数と時間に対する偏微分方程式を解きます。例の pdex1、pdex2、pdex3、pdex4 および pdex5 は、pdepe の使用方法に関するミニチュートリアルです。

この例の問題は関数 pdex1pde、pdex1ic および pdex1bc を使用します。

pdex1pde は、微分方程式を定義します。

$π^{2} \frac{\partial u}{\partial t} = \frac{\partial}{\partial x} (\frac{\partial u}{\partial x}) .$

type pdex1pde

function [c,f,s] = pdex1pde(x,t,u,DuDx)
%PDEX1PDE  Evaluate the differential equations components for the PDEX1 problem.
%
%   See also PDEPE, PDEX1.

%   Lawrence F. Shampine and Jacek Kierzenka
%   Copyright 1984-2014 The MathWorks, Inc.

c = pi^2;
f = DuDx;
s = 0;

pdex1ic は、初期条件を設定します。

$u (x, 0) = \sin π x .$

type pdex1ic

function u0 = pdex1ic(x)
%PDEX1IC  Evaluate the initial conditions for the problem coded in PDEX1.
%
%   See also PDEPE, PDEX1.

%   Lawrence F. Shampine and Jacek Kierzenka
%   Copyright 1984-2014 The MathWorks, Inc.

u0 = sin(pi*x);

pdex1bc は、境界条件を設定します。

$u (0, t) = 0,$

$π e^{- t} + \frac{\partial}{\partial x} u (1, t) = 0 .$

type pdex1bc

function [pl,ql,pr,qr] = pdex1bc(xl,ul,xr,ur,t)
%PDEX1BC  Evaluate the boundary conditions for the problem coded in PDEX1.
%
%   See also PDEPE, PDEX1.

%   Lawrence F. Shampine and Jacek Kierzenka
%   Copyright 1984-2014 The MathWorks, Inc.

pl = ul;
ql = 0;
pr = pi * exp(-t);
qr = 1;

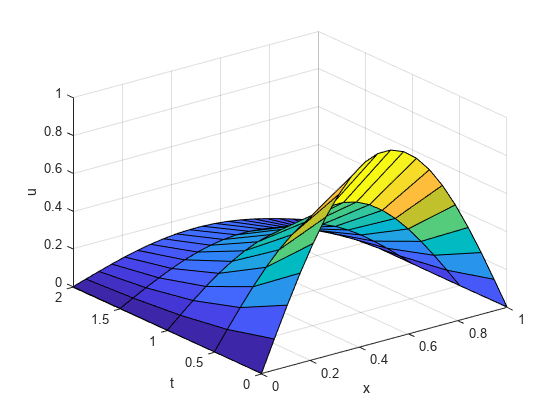
pdepe は、空間の離散化 x と、時間ベクトル t (解のスナップショットで必要) を必要とします。20 の接点のメッシュを使用して問題を解き、t の 5 つの値における解を要求します。解の最初の要素を抽出してプロットします。

x = linspace(0,1,20);
t = [0 0.5 1 1.5 2];
sol = pdepe(0,@pdex1pde,@pdex1ic,@pdex1bc,x,t);

u1 = sol(:,:,1);

surf(x,t,u1);
xlabel('x');
ylabel('t');
zlabel('u');

Figure contains an axes object. The axes object contains an object of type surface.

参考

ode45 | bvp4c | pdepe

微分方程式

開始値問題

境界値問題

遅延微分方程式

偏微分方程式

参考

関連するトピック