map 関数の作成

MapReduce における map 関数の役割

mapreduce は、データのブロックを受け取って中間結果を出力する入力 map 関数と、中間結果を読み取って最終結果を生成する入力 reduce 関数の両方を必要とします。したがって、map 関数および reduce 関数が独立して実行できるように、計算を 2 つの関係する部分に分割するのは自然なことです。たとえば、データ セット内の最大値を求めるために、map 関数は入力データの各ブロック内の最大値を求めることができ、次に、reduce 関数はすべての中間最大値の中から単一の最大値を求めることができます。

次の図に、mapreduce アルゴリズムの Map フェーズを示します。

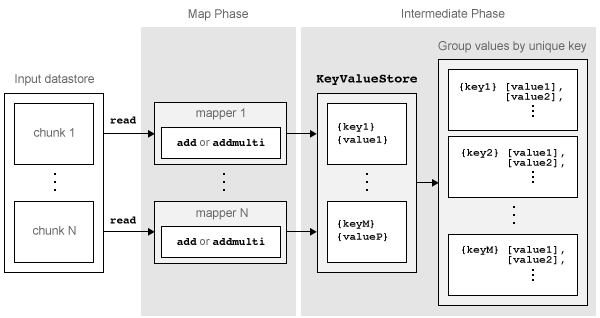
mapreduce アルゴリズムの Map フェーズには次のステップがあります。

1. mapreduce は、関数 read を入力データストアに対し使用してデータのブロックを 1 つ読み取り、そのブロックを処理するために map 関数を呼び出します。

2. 次に、map 関数は個々のデータのブロックを処理し、関数 add または関数 addmulti を使用して中間 KeyValueStore オブジェクトに 1 つ以上のキーと値のペアを追加します。

3. mapreduce はこのプロセスを入力データストア内のデータのブロックごとに繰り返すため、map 関数の呼び出し回数の合計は、データのブロック数と同じになります。データストアの ReadSize プロパティによってデータ ブロックの数が決まります。

mapreduce アルゴリズムの Map フェーズは、map 関数が入力データストア内のデータの各ブロックを処理すると完了します。mapreduce アルゴリズムのこのフェーズの結果は、map 関数が追加したすべてのキーと値のペアを含む KeyValueStore オブジェクトです。Map フェーズの後、mapreduce は KeyValueStore オブジェクト内のすべての値を一意なキーでグループ化して、Reduce フェーズの準備をします。

map 関数の要件

mapreduce は、入力データストア内のデータのブロックごとに、自動的に map 関数を呼び出します。map 関数は、この自動呼出しの際に適切に実行できるように、特定の基本的な要件を満たさなければなりません。これらの要件は、mapreduce アルゴリズムの Map フェーズ中にデータが適切に移動することを集合的に保証します。

map 関数への入力は、data、info および intermKVStore です。

• data および info は、入力データストアに対して関数 read を呼び出した結果です。この呼び出しは、map 関数を呼び出す前に毎回 mapreduce が自動的に実行します。

• intermKVStore は、map 関数がキーと値のペアを追加する必要のある中間 KeyValueStore オブジェクトの名前です。関数 add および addmulti は、このオブジェクト名を使用してキーと値のペアを追加します。map 関数が intermKVStore オブジェクトにキーと値のペアをまったく追加しなかった場合は、mapreduce は reduce 関数を呼び出さず、結果のデータストアは空になります。

map 関数に関するこれらの基本要件に加えて、map 関数によって追加されるキーと値のペアも、以下の条件を満たさなければなりません。

1. キーは数値スカラー、文字ベクトル、または string でなければなりません。数値キーに NaN、複素数、論理値、スパースは使用できません。

2. map 関数で追加されるキーはすべて同じクラスでなければなりません。

3. 値には、有効な MATLAB^® データ型を始めとする任意の MATLAB オブジェクトが使用できます。

メモ

上記のキーと値のペアの要件は、mapreduce を使用する製品によって異なる場合があります。使用する製品のドキュメンテーションで、キーと値のペアに関する製品固有の要件を確認してください。

map 関数の例

以下は、mapreduce の例に使用されているいくつかの分かりやすい map 関数です。

同一の map 関数

mapreduce から渡されたものをそのまま返す map 関数は、"同一のマッパー" と呼ばれます。同一のマッパーは、reduce 関数で計算を実行する前に、一意なキーによる値のグループ化を利用する場合に便利です。identityMapper マッパー ファイルは、例MapReduce を使用する tall QR (TSQR) 行列の因数分解で使用されているマッパーの 1 つです。

function identityMapper(data, info, intermKVStore)
  % This mapper function simply copies the data and add them to the
  % intermKVStore as intermediate values.
  x = data.Value{:,:};
  add(intermKVStore,'Identity', x);
end

単純な map 関数

同一でないマッパーの最も単純な例の 1 つに maxArrivalDelayMapper があります。これは、例MapReduce を使用した最大値の検索のマッパーです。このマッパーは、入力データの各チャンクに対して、最大到着遅延時間を計算してキーと値のペアを中間 KeyValueStore に追加します。

function maxArrivalDelayMapper (data, info, intermKVStore)
  partMax = max(data.ArrDelay);
  add(intermKVStore, 'PartialMaxArrivalDelay',partMax);
end

高度な map 関数

より高度なマッパーの例には statsByGroupMapper があります。これは、例MapReduce を使用してグループごとの要約統計量を計算するのマッパーです。このマッパーは、入れ子関数を使用して、入力データの各チャンクに対していくつかの統計量 (カウント、平均、分散など) を計算し、いくつかのキーと値のペアを中間 KeyValueStore オブジェクトに追加します。また、このマッパーは 4 つの入力引数を使用しますが、mapreduce は 3 つの入力引数をもつ map 関数しか受け入れません。これを回避するには、例で概説しているように、mapreduce の呼び出しの際に無名関数を使用して追加のパラメーターを渡します。

function statsByGroupMapper(data, ~, intermKVStore, groupVarName)
  % Data is a n-by-3 table. Remove missing values first
  delays = data.ArrDelay;
  groups = data.(groupVarName);
  notNaN =~isnan(delays);
  groups = groups(notNaN);
  delays = delays(notNaN);
  % Find the unique group levels in this chunk
  [intermKeys,~,idx] = unique(groups, 'stable');
  % Group delays by idx and apply @grpstatsfun function to each group
  intermVals = accumarray(idx,delays,size(intermKeys),@grpstatsfun);
  addmulti(intermKVStore,intermKeys,intermVals);
  function out = grpstatsfun(x)
    n = length(x); % count
    m = sum(x)/n; % mean
    v = sum((x-m).^2)/n; % variance
    s = sum((x-m).^3)/n; % skewness without normalization
    k = sum((x-m).^4)/n; % kurtosis without normalization
    out = {[n, m, v, s, k]};
  end
end

参考

mapreduce | tabularTextDatastore | add | addmulti | KeyValueStore

関連するトピック

• reduce 関数の作成
• MapReduce 入門