このページは機械翻訳を使用して翻訳されました。元の英語を参照するには、ここをクリックします。
等角線と大円の比較
平面上のラインは一定の傾斜を持ち、2 点間の最短経路を表します。球面上のラインは一定の傾斜を持つことも、2 点間の最短経路を表すこともできますが、必ずしもその両方であるとは限りません。球面上の線の傾斜が一定(方位角が一定)の場合、その線は 等角線 の経路をたどります。球面上のラインが 2 点間の最短経路を表す場合、そのラインは 大円 の経路をたどります。
この図は、大円線と等角線によって接続された 2 つの離れた場所を示しています。
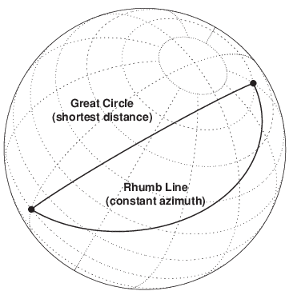
等角線
等角線は、航程線 とも呼ばれ、方位角が一定である曲線です。方位角は、線が子午線となす角度であり、北から時計回りに測定されます。
すべての緯線は、経線と 90° の角度で交差するため、等角線です。さらに、すべての経線は等角線です。
一般に、等角線はいずれかの極に向かって螺旋状に伸びます。等角線の方位角が真の東、西、北、または南である場合、等角線はそれ自身と接続して小円または一対の対蹠子午線を形成します。
等角線は、ルートに沿って方位角が変化しないため、ナビゲーションに役立ちます。等角線の経路は大円経路よりも長くなりますが、方位が一定であるため等角線の経路の方がナビゲートしやすくなります。
大円
大円は、球面と球の中心を通る平面との交点によって定義される、球面に沿った 2 点間の最短経路です。大円は常に球を二等分します。
赤道とすべての子午線は、大円と等角線の両方です。その他の大円は方位角が一定ではないため、等角線ではありません。代わりに、それらは異なる角度で連続する子午線を横切ります。
大円は測地線の例です。測地線は、楕円体上の最短経路など、曲面上の 2 点間の最短経路です。
大円は一般に、方位がルートに沿って変化するため、航海にはあまり役立ちません。大円軌道は等角線軌道よりも短いですが、方位の変化により大円軌道のナビゲートが難しくなります。
関数で等角線と大円を使用する
いくつかの幾何測地学関数を使用すると、パスが等角線に沿っているか大円に沿っているかを指定できます。たとえば、track2 関数を使用して、等角線または大円経路に沿ってトラック ポイントを生成できます。distance 関数を使用して、2 点を結ぶ等角線または大円経路の長さを調べることもできます。