flatearthpoly
Clip polygon to world limits
Syntax
[latf,lonf] = flatearthpoly(lat,lon)
[latf,lonf] = flatearthpoly(lat,lon,longitudeOrigin)
Description
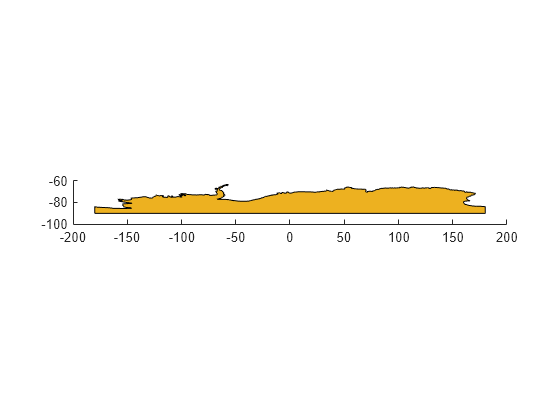
[latf,lonf] = flatearthpoly(lat,lon) trims
NaN-separated polygons specified by the latitude and longitude
vectors lat and lon to the limits [-180
180] in longitude and [-90 90] in latitude, inserting
straight segments along the +/- 180-degree meridians and at the poles. Inputs and
outputs are in degrees.
Display functions automatically cut and trim geographic data when required by the map
projection. Use the flatearthpoly function only when performing set
operations on polygons.
[latf,lonf] = flatearthpoly(lat,lon,longitudeOrigin) centers
the longitude limits on the longitude specified by the scalar longitude longitudeOrigin.
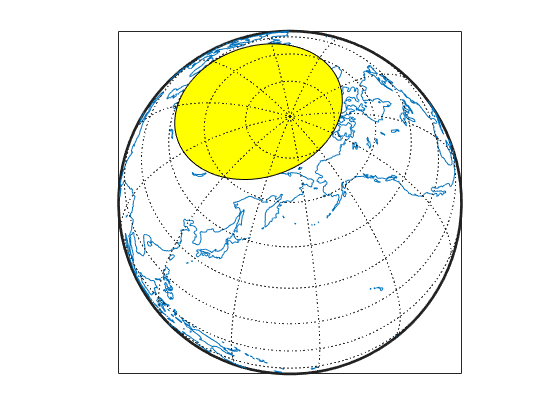
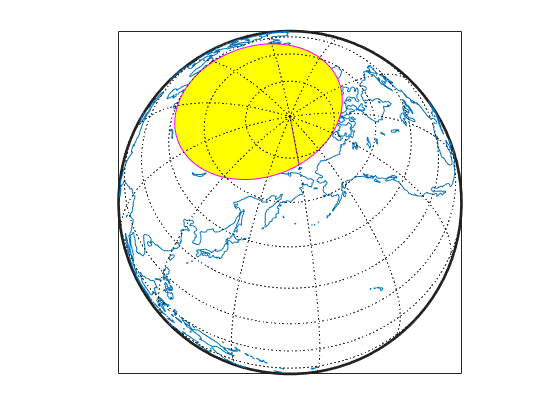
Examples
Tips
The polygon defined by lat and lon must be well-formed:
The boundaries must not intersect.
The vertices of outer boundaries must be in a clockwise order and the vertices of inner boundaries must be in a counterclockwise order, such that the interior of the polygon is always to the right of the boundary.
For more information, see Create and Display Polygons.
Version History
Introduced before R2006a