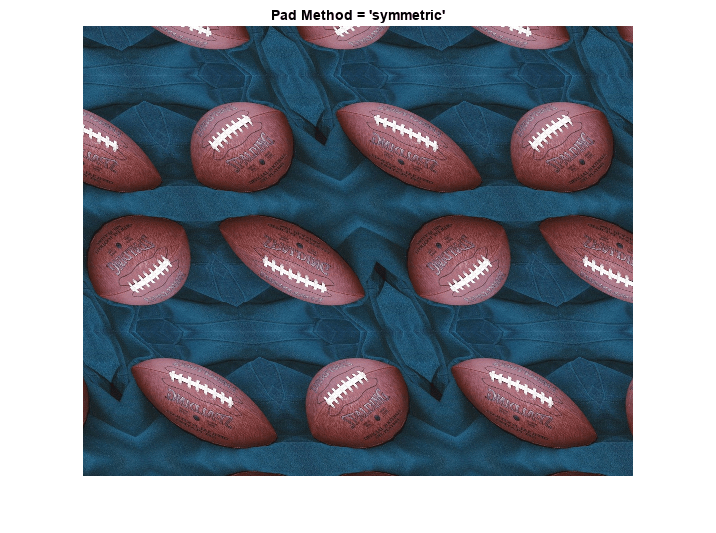イメージのパディングとせん断の同時実行
この例では、単純せん断変換を表す tform struct を作成し、イメージに適用する方法を示します。変換が直線と円にどのような影響を与えるかを調査し、その後、imtransform および tformarray と併用できるイメージのパディングのさまざまなオプションを調査するための手段としてそれを使用します。
手順 1: 単純せん断を使用したイメージの変換
2 次元では、入力座標 [u v] のペアを出力座標 [x y] のペアにマッピングする単純せん断変換は、
ここで、a は定数です。
簡単なせん断は、アフィン変換の特殊なケースです。以下の
が、最初の 2 つの方程式から得た x および y の値を出力するかどうかは、簡単に確認できます。
a = 0.45 に設定し maketform を使用してアフィン tform struct を作成します。
a = 0.45;
T = maketform('affine', [1 0 0; a 1 0; 0 0 1] );変換するイメージを選択し、読み取り、表示します。
A = imread('football.jpg'); h1 = figure; imshow(A); title('Original Image');

塗りつぶしの値としてオレンジの陰影を選択します。
orange = [255 127 0]';
T を使用して A を変換する用意ができました。imtransform を以下のようにして呼び出すこともできました。
B = imtransform(A,T,'cubic','FillValues',orange);
ただし、行と列両方に 3 次内挿を適用するため、この処理は無駄です (純粋せん断変換では、各行への内挿のみが必要です)。その代わり、行に 3 次内挿を適用して、列には単に最近傍内挿を使用するリサンプリング方法を作成および使用し、imtransform を呼び出して結果を表示します。
R = makeresampler({'cubic','nearest'},'fill');
B = imtransform(A,T,R,'FillValues',orange);
h2 = figure; imshow(B);
title('Sheared Image');
手順 2: 変換の探求
直線グリッドまたは円配列を関数 tformfwd で変換するのは、変換を理解するために良い方法です (フォワード関数および逆関数がある限り)。
元のイメージを覆う線のグリッドを定義し、それをイメージ上に表示します。次に関数 tformfwd を使用して、グリッドの各線に純粋なせん断を適用し、せん断されたイメージ上に結果を表示します。
[U,V] = meshgrid(0:64:320,0:64:256); [X,Y] = tformfwd(T,U,V); gray = 0.65 * [1 1 1]; figure(h1); hold on; line(U, V, 'Color',gray); line(U',V','Color',gray);

figure(h2); hold on; line(X, Y, 'Color',gray); line(X',Y','Color',gray);

円の配列でも同様に実行できます。
gray = 0.65 * [1 1 1]; for u = 0:64:320 for v = 0:64:256 theta = (0 : 32)' * (2 * pi / 32); uc = u + 20*cos(theta); vc = v + 20*sin(theta); [xc,yc] = tformfwd(T,uc,vc); figure(h1); line(uc,vc,'Color',gray); figure(h2); line(xc,yc,'Color',gray); end end


手順 3: パディング手法 'fill'、'replicate' および 'bound' の比較
せん断変換の適用時、関数 imtransform は、データのないオレンジ色の三角形を左から右に塗りつぶしました。それは、関数 makeresampler の呼び出し時にパディング手法 'fill' を指定したからです。パディング手法には、合計 5 つの選択肢があります ('fill'、'replicate'、'bound'、'circular'、および 'symmetric')。ここでは、最初の 3 つを比較してみます。
まずオプション 'fill' の機能を理解するために、imtransform のオプション 'XData' および 'YData' を使用して、出力イメージに強制的に空間を追加します。
R = makeresampler({'cubic','nearest'},'fill');
Bf = imtransform(A,T,R,'XData',[-49 500],'YData',[-49 400],...
'FillValues',orange);
figure, imshow(Bf);
title('Pad Method = ''fill''');
ここでメソッド 'replicate' (この場合は塗りつぶし値を指定する必要なし) を実行します。
R = makeresampler({'cubic','nearest'},'replicate');
Br = imtransform(A,T,R,'XData',[-49 500],'YData', [-49 400]);
figure, imshow(Br);
title('Pad Method = ''replicate''');
さらにメソッド 'bound' を試行します。
R = makeresampler({'cubic','nearest'}, 'bound');
Bb = imtransform(A,T,R,'XData',[-49 500],'YData',[-49 400],...
'FillValues',orange);
figure, imshow(Bb);
title('Pad Method = ''bound''');
'fill' および 'bound' の結果は同じように見えますが、よく見ると 'fill' の方がエッジが滑らかなことに気が付きます。これは、入力イメージが塗りつぶし値でパディングされ、3 次内挿がエッジ、埋め込み値、およびイメージ値全体に適用されたからです。それと比較して、メソッド 'bound' は入力イメージの内側と外側を厳密に区別します。外側のポイントは塗りつぶされます。内側のポイントは、エッジに近い場合、反復を利用して内挿されます。近くで見ると、より明確に表示することができます。XData および YData を選択してイメージの右下隅に近いポイントを囲み、出力イメージ空間で 'nearest' を使用してサイズ変更し、各ピクセルの表示方法を保存します。
R = makeresampler({'cubic','nearest'},'fill');
Cf = imtransform(A,T,R,'XData',[423 439],'YData',[245 260],...
'FillValues',orange);
R = makeresampler({'cubic','nearest'},'bound');
Cb = imtransform(A,T,R,'XData',[423 439],'YData',[245 260],...
'FillValues',orange);
Cf = imresize(Cf,12,'nearest');
Cb = imresize(Cb,12,'nearest');
figure;
subplot(1,2,1); imshow(Cf); title('Pad Method = ''fill''');
subplot(1,2,2); imshow(Cb); title('Pad Method = ''bound''');
手順 4: パディング手法 'circular' および 'symmetric' の実行
残りの 2 つのパディング手法は、'circular' (各次元での巡回的な繰り返し) および 'symmetric' (付加された鏡像とのイメージの巡回的な繰り返し) です。発生するパターンをより多く示すため、変換を再定義してスケールを半分にします。
Thalf = maketform('affine',[1 0; a 1; 0 0]/2); R = makeresampler({'cubic','nearest'},'circular'); Bc = imtransform(A,Thalf,R,'XData',[-49 500],'YData',[-49 400],... 'FillValues',orange); figure, imshow(Bc); title('Pad Method = ''circular''');
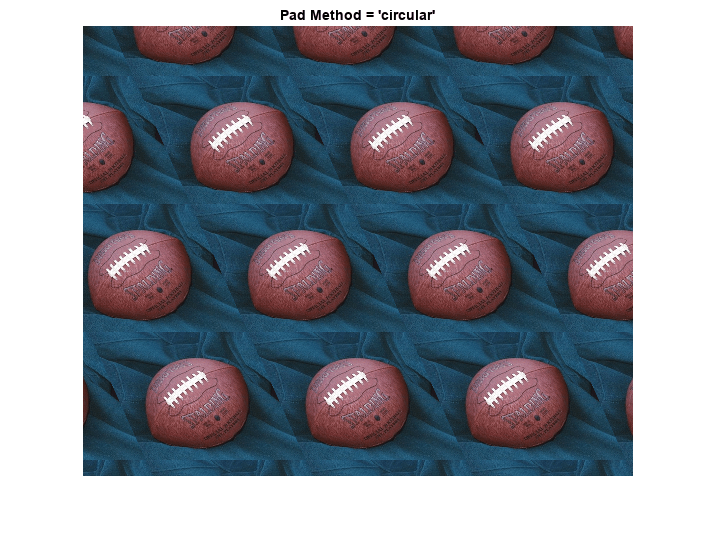
R = makeresampler({'cubic','nearest'},'symmetric');
Bs = imtransform(A,Thalf,R,'XData',[-49 500],'YData',[-49 400],...
'FillValues',orange);
figure, imshow(Bs);
title('Pad Method = ''symmetric''');