雪片の粒度分布

この例では、粒度分布を使用してイメージ内の雪片のサイズ分布を計算する方法を示します。粒度分布は、最初に各オブジェクトを明示的にセグメント化 (検出) せずにイメージ内のオブジェクトの大きさの分布を決定します。

イメージの読み取り

snowflakes.png イメージを読み取ります。これは雪片の写真です。

I = imread("snowflakes.png");
imshow(I)

コントラストの強調

最初の手順では、イメージでの強度コントラストを最大化します。これを実行するには、コントラストを制限する適応ヒストグラム均等化を実行する関数 adapthisteq を使用します。データ型の全ダイナミックレンジを満たすように、関数 imadjust を使用してイメージ強度を再スケーリングします。

claheI = adapthisteq(I,"NumTiles",[10 10]);
claheI = imadjust(claheI);
imshow(claheI)

強調されたイメージでのイメージ表面下ボリュームの決定

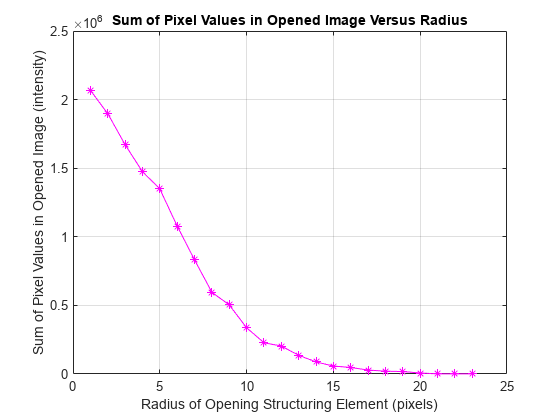
粒度分布は、石をいくつかの "ふるい" にかける操作に似ています。ふるいのサイズを増加させながら、ふるいにかけるたびに残っているものを収集します。粒度分布では、サイズが増加する一連のモルフォロジーオープニングが適用され、各オープニングの後にイメージピクセル値の合計が計算されます。グレースケールイメージの場合、この合計はピクセル強度値によって高さが決まる表面の下のボリュームに相当します。ボリュームは、オープニングごとに少なくなります。これは、大きさが増していく構造化要素によって、より大きなオブジェクトが取り除かれるためです。

オプションとして、表面ボリュームの概念を理解するために、雪片イメージの表面強度をプロットできます。垂直方向の縦横比を調整して、表面全体が見えるようにします。表面のピークは、元の 2 次元イメージの明るい部分に相当します。

figure
surf(claheI, EdgeColor="none")
colormap("gray")
title("Snowflakes Pixel Intensity Surface")
daspect([1 1 15]);

構造化要素のサイズを増大させると表面ボリューム強度がゼロになるように、カウンターの制限を選択します。表示目的のために、表面積配列の最初のエントリは空白にします。

radius_range = 0:22;
intensity_volume = zeros(size(radius_range));
for counter = radius_range
    remain = imopen(claheI, strel("disk", counter));
    intensity_volume(counter + 1) = sum(remain(:));  
end
figure
plot(intensity_volume, "m - *")
grid on
title("Sum of Pixel Values in Opened Image Versus Radius")
xlabel("Radius of Opening Structuring Element (pixels)")
ylabel("Sum of Pixel Values in Opened Image (intensity)")

分布の導関数の推定

2 回連続したオープニング間で表面ボリューム強度が大幅に下がる場合は、イメージに小さいオープニングと同じようなサイズのオブジェクトがあるということです。これは、半径に対する表面ボリューム強度の導関数と等しく、イメージ内の雪片のサイズ分布が含まれています。関数 diff を使用して導関数を推定します。

intensity_volume_prime = diff(intensity_volume);
figure
plot(intensity_volume_prime, "m - *")
grid on
title("Granulometry (Size Distribution) of Snowflakes")
ax = gca;
ax.XTick = [0 2 4 6 8 10 12 14 16 18 20 22];
xlabel("Radius of Snowflakes (pixels)")
ylabel("Derivative of Sum of Pixel Values (intensity/pixel)")

特定の半径をもつ雪片の強調

グラフの局部的最小値とその半径の値に注意してください。局部的最小値により、その半径をもっている雪片があることが分かります。最小ポイントが負になると、その半径での雪片の累積強度が大きくなります。たとえば、負の最小ポイントは、5 ピクセルの半径マークで発生します。5 ピクセルの半径の雪片は、次の手順で強調できます。

open5 = imopen(claheI,strel("disk",5));
open6 = imopen(claheI,strel("disk",6));
rad5 = open5 - open6;
imshow(rad5,[])

参考

adapthisteq | imadjust | imopen | strel