非線形リグレッサーおよびカスタム リグレッサーを含む非線形 ARX モデルの作成
この例では、非線形 ARX (IDNLARX) モデルで多項式リグレッサーおよびカスタム リグレッサーを使用する方法を説明します。
はじめに
DNLARX モデルでは、各出力がリグレッサーの関数となります。リグレッサーは、過去の入力および出力を変換したものです。一般的なリグレッサーは、"linearRegressor" 仕様オブジェクトで表される遅延した入力変数または出力変数、または "polynomialRegressor" オブジェクトで表される遅延した変数の多項式です。ただし、絶対値 (例: "abs(y(t-1))") を課する機能以外に、これらの種類のリグレッサーを使用して複雑な数式は作成できません。たとえば、出力関数に形式 "sin(u(t-3)).*exp(-abs(u(t)))" のリグレッサーが必要な場合、リグレッサーの式にカスタマイズした公式を入力する方法が必要です。これは "customRegressor" オブジェクトを使用すると簡単です。その名が示すように、customRegressor オブジェクトを使用して、任意のカスタマイズした公式を非線形 ARX モデルのリグレッサーとして組み込みます。
電圧 "V" と電流 "I" を入力としてもつ電気系統を例として考えてみます。電力が電気系統の重要な数値を占める場合、カスタムのリグレッサー "V*I" を作成する方が理にかなっています。線形リグレッサーや多項式リグレッサーだけを使用するよりも、適切に定義したカスタムのリグレッサーを使用した方が効率が良い場合があります。
SISO の例: 内燃エンジンのモデル化
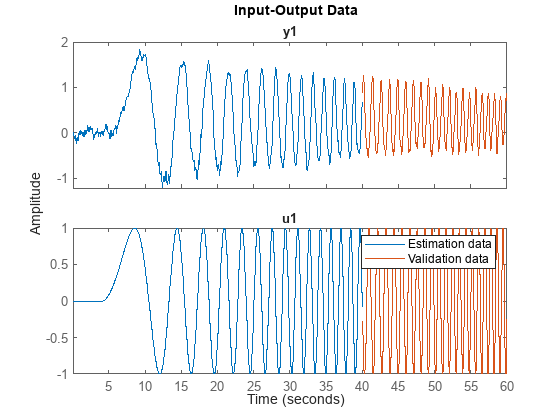
ファイル icEngine.mat には、サンプリング レート 0.04 秒で収集した 1500 の入力/出力サンプルによる 1 つのデータセットが含まれます。入力 u(t) は、By-Pass Idle Air Valve (BPAV) を制御する電圧 [V] で、出力 y(t) は、エンジン速度 [RPM/100] です。データを読み込み、モデル推定用のデータセット "ze" と、モデル検証用のデータセット "zv" に分割します。
load icEngine z = iddata(y,u,0.04); ze = z(1:1000); zv = z(1001:1500); plot(ze,zv) legend('Estimation data','Validation data')
ARX 次数としての線形リグレッサー
次数行列 [na nb nk] は、線形 ARX モデルでも使用され、線形リグレッサーの容易な定義に役立ちます。このリグレッサーは、特定のサンプル数だけ遅延された入出力変数です。モデル次数を選択するには、試行錯誤が必要となります。この例では、[na nb nk] = [4 2 10] を使用します。これは、線形リグレッサー y(t-1)、y(t-2)、y(t-3)、y(t-4)、u(t-10)、u(t-11) に対応します。モデル出力が 6 個のリグレッサーの加重合計にオフセットを加えたものになるように、線形出力関数を選択します。

sys0 = nlarx(ze, [4 2 10], idLinear);
このモデルの入力名、出力名、およびリグレッサー リストを以下に示します。既定の名前 'u1'、'y1' が使用されています。
sys0.InputName
ans = 1×1 cell array
{'u1'}
sys0.OutputName
ans = 1×1 cell array
{'y1'}
disp(getreg(sys0))
{'y1(t-1)' }
{'y1(t-2)' }
{'y1(t-3)' }
{'y1(t-4)' }
{'u1(t-10)'}
{'u1(t-11)'}
これらは "線形" リグレッサーです。モデルの [リグレッサー] プロパティに linearRegressor オブジェクトとして保存されています。
sys0.Regressors
ans =
Linear regressors in variables y1, u1
Variables: {'y1' 'u1'}
Lags: {[1 2 3 4] [10 11]}
UseAbsolute: [0 0]
TimeVariable: 't'
Regressors described by this set
"リグレッサー" プロパティは、暗黙的に回帰仕様オブジェクトを使用するリグレッサーに関する情報を格納します。次数行列 [4 2 10] は、線形リグレッサーを指定する簡便な方法と見なせます。ここでラグは連続で、出力変数の最小ラグは 1 に固定されています。
linearRegressor 仕様オブジェクトを使用した線形リグレッサー
任意のラグをもつ変数を選択できる、より柔軟な方法は "linearRegressor" オブジェクトを使用することです。上記の構成では、変数 y1 はラグ [1 2 3 4] を持つのに対して、変数 u1 はラグ [10 11] を持ちます。linearRegressor オブジェクトを使用すると、以下のように同じ構成を達成できます。
LinReg = linearRegressor({'y1','u1'}, {1:4, [10, 11]});
sys1 = nlarx(ze, LinReg, idLinear)sys1 = Nonlinear ARX model with 1 output and 1 input Inputs: u1 Outputs: y1 Regressors: Linear regressors in variables y1, u1 List of all regressors Output function: Linear with offset Sample time: 0.04 seconds Status: Estimated using NLARX on time domain data "ze". Fit to estimation data: 94.35% (prediction focus) FPE: 0.001877, MSE: 0.00183 Model Properties
モデル sys1 および sys0 の推定構文を比較します。sys1 の作成時に、次数行列を線形リグレッサーの仕様オブジェクトに置き換えます。得られるモデル sys0 および sys1 は同一です。
[getpvec(sys0), getpvec(sys1)] % estimated parameter vectors of sys0 and sys1ans = 7×2
0.7528 0.7528
0.0527 0.0527
-0.0621 -0.0621
-0.0425 -0.0425
-0.0165 -0.0165
-0.0289 -0.0289
-0.0000 -0.0000
linearRegressor オブジェクトを使用し、次のシナリオで次数行列の代わりにリグレッサーを指定します。
セット のような変数に任意の (不連続) ラグの使用
出力変数の最小ラグを 1 以外に設定。たとえば、セット
セット のような変数の絶対値の使用。ここで使用されるのは変数 'y1' の絶対値のみ。これは以下のように達成可能
LinRegWithAbs = linearRegressor({'y1','u1'},{[1 10], [0 2]},[true, false])LinRegWithAbs =
Linear regressors in variables y1, u1
Variables: {'y1' 'u1'}
Lags: {[1 10] [0 2]}
UseAbsolute: [1 0]
TimeVariable: 't'
Regressors described by this set
多項式のリグレッサー
多くの場合、遅延 I/O 変数の多項式であるリグレッサーが必要です。これらは "polynomialRegressor" オブジェクトを使用して、モデルに追加できます。、 をリグレッサーとしてモデルに追加するとします。最初に、これらの設定で仕様オブジェクトを作成し、それからこのオブジェクトをモデルに追加します。
% Create order 2 regressors in variables 'u1' and 'y1', with lags 10 and 1 % respectively PolyReg = polynomialRegressor({'u1','y1'},{10, 1},2); % Use LinReg and PolyReg in the model sys2 = nlarx(ze, [LinReg; PolyReg], idLinear)
sys2 = Nonlinear ARX model with 1 output and 1 input Inputs: u1 Outputs: y1 Regressors: 1. Linear regressors in variables y1, u1 2. Order 2 regressors in variables u1, y1 List of all regressors Output function: Linear with offset Sample time: 0.04 seconds Status: Estimated using NLARX on time domain data "ze". Fit to estimation data: 94.47% (prediction focus) FPE: 0.001804, MSE: 0.001752 Model Properties
カスタマイズした式に基づくリグレッサー
線形リグレッサーおよび多項式リグレッサーが最も一般的に使用されますが、多項式では記述されない別の式を使用することが必要になる場合もあります。たとえば、 のような三角関数です。もう 1 つの例は、飽和関数 です。このような状況では、特定の数式をカプセル化する customRegressor オブジェクトの配列を使用できます。
以下の例では、リグレッサーは、変数名 'u1' および遅延サンプル 10 の余弦関数として作成しています。すなわち、 です。最後の入力引数の論理値は、このカスタムのリグレッサーがベクトル化されているかどうかを示します。ベクトル化されたリグレッサーは、計算時間が速くてすみますが、最初の入力引数で示される関数に注意が必要です。
x = customRegressor('u1', 10, @cos)x =
Custom regressor: cos(u1(t-10))
VariablesToRegressorFcn: @cos
Variables: {'u1'}
Lags: {[10]}
Vectorized: [1]
TimeVariable: 't'
Regressors described by this set
指定した式 (ここでは @cos) は、リグレッサー オブジェクトの VariablesToRegressorFcn プロパティに保存されます。既定では、関数の評価はベクトル化されると仮定されます。すなわち、入力が N 行の行列の場合、関数 x.VariablesToRegressorFcn の出力は長さ N の列ベクトルになります。ベクトル化により、モデルの推定およびシミュレーションのプロセス中に、リグレッサーの評価が高速化します。ただし、必要であれば、Vectorized プロパティを FALSE に設定することで無効にする方法もあります。
全体で同じ基となる式を共有しながら、異なるラグ値を使用するリグレッサーの配列を作成できます。たとえば、式が であるとします。ここで 'u' および 'y' は測定データが利用可能な 2 変数であり、ラグ (a,b) は範囲 1:10 で複数の値をとることができます。customRegressor コンストラクターの 1 回の呼び出しで、これらのリグレッサーの配列を作成できます。
C = customRegressor({'u','y'},{1:10, 1:10}, @(x,y)x.*abs(y))C =
Custom regressor: @(x,y)x.*abs(y)
VariablesToRegressorFcn: @(x,y)x.*abs(y)
Variables: {'u' 'y'}
Lags: {[1 2 3 4 5 6 7 8 9 10] [1 2 3 4 5 6 7 8 9 10]}
Vectorized: [1]
TimeVariable: 't'
Regressors described by this set
C は、式 を使用して範囲 1:10 にある 値および 値のすべての組み合わせに対して生成された 100 個のリグレッサーのセットを表します。
モデルにある全 3 種類のリグレッサーを IC エンジン ダイナミクスに使用
試行錯誤または物理的な考察により、モデルでリグレッサー セット を使う必要が示唆されているとします。線形式、多項式、三角関数式が混在しています。以下のように進めます。
LinReg = linearRegressor('y1',1); PolyReg = polynomialRegressor('u1',[10 11],3); CustomReg = customRegressor('y1',4,@(x)sin(x)); % for now no nonlinearity; output is a linear function of regressors sys3 = nlarx(ze,[LinReg; PolyReg; CustomReg], [])
sys3 = Nonlinear ARX model with 1 output and 1 input Inputs: u1 Outputs: y1 Regressors: 1. Linear regressors in variables y1 2. Order 3 regressors in variables u1 3. Custom regressor: sin(y1(t-4)) List of all regressors Output function: Linear with offset Sample time: 0.04 seconds Status: Estimated using NLARX on time domain data "ze". Fit to estimation data: 92.11% (prediction focus) FPE: 0.003647, MSE: 0.00357 Model Properties
getreg(sys3)
ans = 4×1 cell
{'y1(t-1)' }
{'u1(t-10)^3' }
{'u1(t-11)^3' }
{'sin(y1(t-4))'}
このワークフローを拡張して、モデルにシグモイド ネットワークのような非線形マッピング関数を含めたり、使用するリグレッサー セットのサブセットのみを線形および非線形コンポーネントの入力に指定したりできます (メモ: シグモイド ネットワークは、線形関数、オフセット項、およびシグモイド ユニットの和である非線形関数からなる 3 つのコンポーネントの合計)。以下の例では、テンプレートモデル ベースのワークフローを使用します。ここでは、テンプレート IDNLARX モデルと推定オプション セットを NLARX コマンドでパラメーター推定に使用する前に、別々に準備します。
sys4 = idnlarx(ze.OutputName, ze.InputName, [4 2 10], idSigmoidNetwork); % generate 'u1(t-10)^2', 'y1(t-1)^2', 'u1(t-10)*y1(t-1)' P = polynomialRegressor({'y1','u1'},{1, 10},2, false, true); % generate cos(u1(t-10)) C1 = customRegressor('u1',10,@cos); % generate sin(y1(t-1).*u1(t-10)+u1(t-11)) C2 = customRegressor({'y1','u1','u1'},{1, 10, 11},@(x,y,z)sin(x.*y+z)); % add the polynomial and custom regressors to the model sys2 sys4.Regressors = [sys4.Regressors; P; C1; C2]; % view the regressors and how they are used in the model disp(sys4.RegressorUsage)
y1:LinearFcn y1:NonlinearFcn
____________ _______________
y1(t-1) true true
y1(t-2) true true
y1(t-3) true true
y1(t-4) true true
u1(t-10) true true
u1(t-11) true true
y1(t-1)^2 true true
u1(t-10)^2 true true
cos(u1(t-10)) true true
sin(y1(t-1).*u1(t-10)+u1(t-11)) true true
% designate only the linear regressors to be used in the nonlinear % component of the sigmoid network Usage = sys4.RegressorUsage; Usage{7:end,2} = false; sys4.RegressorUsage = Usage; disp(sys4.RegressorUsage)
y1:LinearFcn y1:NonlinearFcn
____________ _______________
y1(t-1) true true
y1(t-2) true true
y1(t-3) true true
y1(t-4) true true
u1(t-10) true true
u1(t-11) true true
y1(t-1)^2 true false
u1(t-10)^2 true false
cos(u1(t-10)) true false
sin(y1(t-1).*u1(t-10)+u1(t-11)) true false
% Prepapre estimation options: use Levenberg-Marquardt solver with 30 maximum iterations. % Turn progress display on and set estimation focus to 'simulation' opt = nlarxOptions; opt.Focus = 'simulation'; opt.Display = 'on'; opt.SearchMethod = 'lm'; opt.SearchOptions.MaxIterations = 30; % estimate parameters of sys4 to fit data ze sys4 = nlarx(ze, sys4, opt)
sys4 = Nonlinear ARX model with 1 output and 1 input Inputs: u1 Outputs: y1 Regressors: 1. Linear regressors in variables y1, u1 2. Order 2 regressors in variables y1, u1 3. Custom regressor: cos(u1(t-10)) 4. Custom regressor: sin(y1(t-1).*u1(t-10)+u1(t-11)) List of all regressors Output function: Sigmoid network with 10 units Sample time: 0.04 seconds Status: Estimated using NLARX on time domain data "ze". Fit to estimation data: 87.81% (simulation focus) FPE: 0.001491, MSE: 0.008517 Model Properties
これで、モデルの応答と検証データセット zv の出力を比較することで、モデルを検証できます。
compare(zv, sys1, sys2, sys3, sys4)
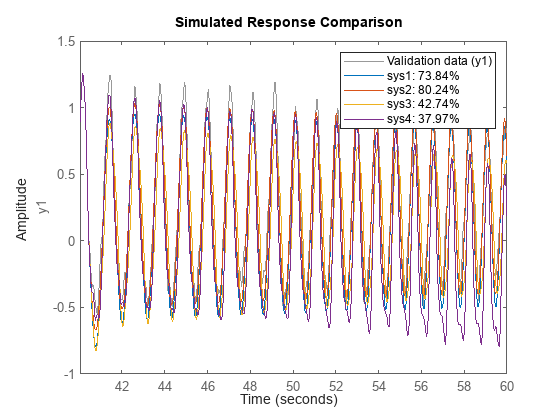
比較プロットは sys2 が最適モデルであることを示しています。この例で使用したリグレッサーは任意に選択されており、その主な目的はリグレッサーを作成し、モデルを推定する別の方法を示すことです。リグレッサーをより適切に選択することで、より良い結果が得られる可能性があります。
MIMO の例: モーター付きカメラのモデル化
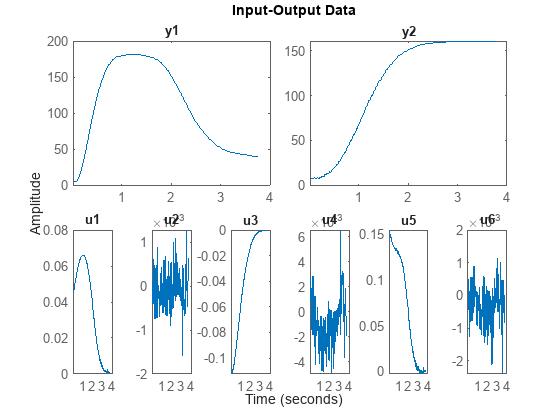
ファイル motorizedcamera.mat には、サンプリング レート 0.02 秒でモーター付きカメラから収集した 188 データ サンプルによる 1 つのデータが含まれます。入力ベクトル u(t) は 6 つの変数で構成されます。これらの変数とは、カメラに固定された直交 X-Y-Z 座標系の 3 つの並進速度成分 [m/s] と、X-Y-Z 軸周りの 3 つの回転速度成分 [rad/s] です。出力ベクトル y(t) は 2 つの変数を含みます。これらの変数は、3D 空間の固定カメラ ポイントから取得したイメージによるポイントの位置 (ピクセル単位) です。IDDATA オブジェクト z を作成し、ロードしたデータを保持します。
load motorizedcamera z = iddata(y, u, 0.02, 'Name', 'Motorized Camera', 'TimeUnit', 's'); plot(z)
MIMO でさまざまな種類のリグレッサーを使用するのは、SISO の場合とあまり違いはありません。すべてのリグレッサーは、システムのすべての出力に対するダイナミクスで使用されています。使用する特定のリグレッサーを特定の出力に割り当てるために、RegressorUsage プロパティを使用できます。
nanbnk = [ones(2,2), 2*ones(2,6), ones(2,6)];
sysMIMO = idnlarx(z.OutputName, z.InputName, nanbnk, idLinear);
C = customRegressor({'u5','u6'},{1 1},@(x,y)x.*y);
P1 = polynomialRegressor('u1',1,2);
P2 = polynomialRegressor('y2',1,3);
sysMIMO.Regressors = [sysMIMO.Regressors; C; P1; P2];
getreg(sysMIMO)ans = 17×1 cell
{'y1(t-1)' }
{'y2(t-1)' }
{'u1(t-1)' }
{'u1(t-2)' }
{'u2(t-1)' }
{'u2(t-2)' }
{'u3(t-1)' }
{'u3(t-2)' }
{'u4(t-1)' }
{'u4(t-2)' }
{'u5(t-1)' }
{'u5(t-2)' }
{'u6(t-1)' }
{'u6(t-2)' }
{'u1(t-1)^2' }
{'y2(t-1)^3' }
{'u5(t-1).*u6(t-1)'}
sysMIMO = nlarx(z, sysMIMO)
sysMIMO = Nonlinear ARX model with 2 outputs and 6 inputs Inputs: u1, u2, u3, u4, u5, u6 Outputs: y1, y2 Regressors: 1. Linear regressors in variables y1, y2, u1, u2, u3, u4, u5, u6 2. Order 2 regressors in variables u1 3. Order 3 regressors in variables y2 4. Custom regressor: u5(t-1).*u6(t-1) List of all regressors Output functions: Output 1: Linear with offset Output 2: Linear with offset Sample time: 0.02 seconds Status: Estimated using NLARX on time domain data "Motorized Camera". Fit to estimation data: [99.05;98.85]% (prediction focus) FPE: 0.2067, MSE: 0.7496 Model Properties
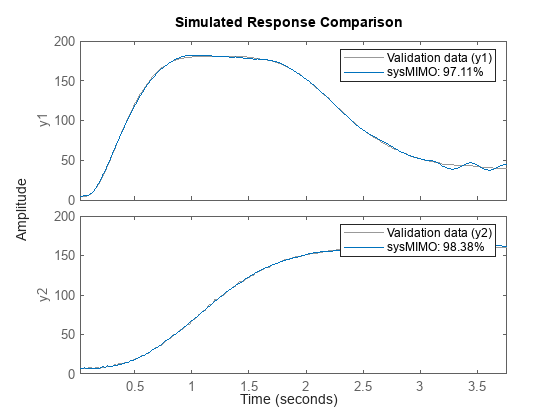
モデル応答を推定データと比較します。
compare(z,sysMIMO)
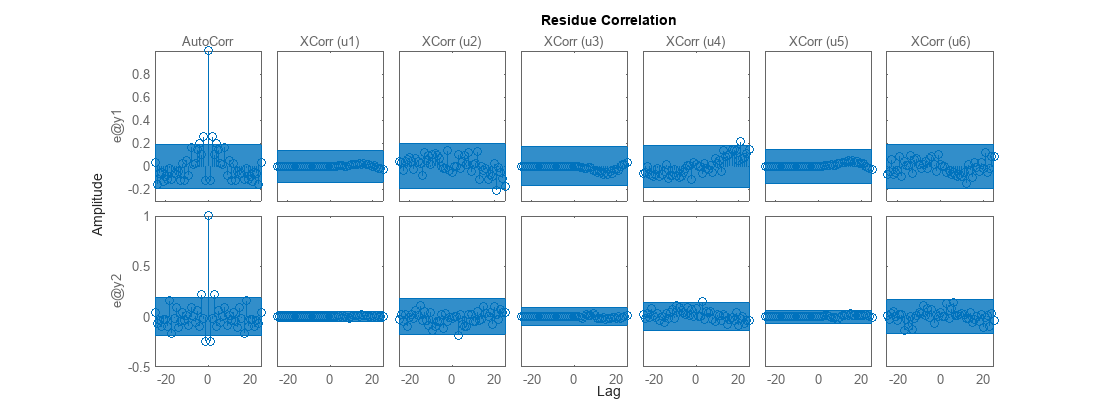
モデル残差を解析し、自己相関 (白色性テスト) および入力信号との相互相関 (相関テスト) を調べます。
fig = figure; fig.Position(3) = 2*fig.Position(3); resid(z,sysMIMO)