3 つの個体群生態系: 時系列の MATLAB と C MEX ファイル モデリング
この例では、非線形グレー ボックス時系列モデルを作成する方法を説明します。時系列モデルは、測定された入力を使用しないモデルです。調査対象となっているのは、理想化された 3 種類の生態系で、2 種の生物が次のいずれかの関係にあります。
同じ食物で競合する
捕食-被食関係にある
この例では、MATLAB® ファイルと C MEX ファイルの両方に基づくモデル化を示します。
個体群生態系
調査対象の 3 つの個体群システムすべてで、2 つの種が時間とともにどのように変化するかに注目します。これをモデル化するには、x1(t) と x2(t) で時刻 t におけるそれぞれの種の数を示します。l1 と l2 で x1(t) と x2(t) それぞれに関連する出生率を示します。これは時間に対して定数と仮定します。種の死亡率は食物の取得率と、捕食者がある場合は捕食されるリスクの両方に依存します。多くの場合 (一般に)、種 i の死亡率 (i = 1 または 2) は ui(x1(t), x2(t)) と記述できます。ここで ui(.) は適切な関数です。実際には、ui(x1(t), x2(t))*xi(t) の種 i が時間単位ごとに死亡することになります。これらの記述の総合した影響は、モデル構造の状態空間タイプでまとめられます (時系列):
d
-- x1(t) = l1*x1(t) - u1(x1(t), x2(t))*x1(t)
dt
d
-- x2(t) = l2*x2(t) - u2(x1(t), x2(t))*x2(t)
dt
ここで、出力として 2 つの状態を選択します。y1(t) = x1(t)、y2(t) = x2(t) とします。
A.1.同じ食物で競合する 2 種の生物
2 つの種が同じ食物で競合する場合、種の全体的な個体群によって食物の取得率が変化し、それによって死亡率も変化します。シンプルで一般的なアプローチは、死亡率を次のように記述できると仮定することです。
ui(x1(t), x2(t)) = gi + di*(x1(t) + x2(t))
両方の種について (i = 1 または 2)、gi と di は不明なパラメーターです。これにより、次の状態空間構造が得られます。
d
-- x1(t) = (l1-g1)*x1(t) - d1*(x1(t)+x2(t))*x1(t)
dt
d
-- x2(t) = (l2-g2)*x2(t) - d2*(x1(t)+x2(t))*x2(t)
dt
この構造からすぐに生じる問題は、l1、g1、l2、g2 を個別に特定できないことです。p1 = l1-g1 および p3 = l2-g2 であることがわかるだけです。p2 = d1、p4 = d2 とすることで、再パラメーター化されたモデル構造が得られます。
d
-- x1(t) = p1*x1(t) - p2*(x1(t)+x2(t))*x1(t)
dt
d
-- x2(t) = p3*x2(t) - p4*(x1(t)+x2(t))*x2(t)
dt
y1(t) = x1(t)
y2(t) = x2(t)
この最初の個体群の例では、MATLAB ファイル モデリングを使用します。上記の方程式が MATLAB ファイルpreys_m.m に、次の定数とともに入力されます。
function [dx, y] = preys_m(t, x, u, p1, p2, p3, p4, varargin) %PREYS_M Two species that compete for the same food. % Output equations. y = [x(1); ... % Prey species 1. x(2) ... % Prey species 2. ]; % State equations. dx = [p1*x(1)-p2*(x(1)+x(2))*x(1); ... % Prey species 1. p3*x(2)-p4*(x(1)+x(2))*x(2) ... % Prey species 2. ];
次に、MATLAB ファイルと初期パラメーター ベクトル、適切な初期状態、一部の管理情報を入力として IDNLGREY オブジェクト コンストラクターに指定します。パラメーターと初期状態の両方の開始値が、それぞれ Npo (パラメーター オブジェクトの数 = すべてのパラメーターがスカラーの場合はパラメーターの数) と Nx (状態の数) を要素とする構造体配列として指定されていることに注意してください。これらの構造体配列を通じて、既定の設定以外のプロパティ値 ('Name'、'Unit'、'Value'、'Minimum'、'Maximum'、'Fixed') を各パラメーターと初期状態に完全に割り当てることができます。ここで、各初期状態の 'Minimum' 値にゼロを割り当て (個体数は正値です!)、また、両方の初期状態を既定で推定するように指定しました。
FileName = 'preys_m'; % File describing the model structure. Order = [2 0 2]; % Model orders [ny nu nx]. Parameters = struct('Name', {'Survival factor, species 1' 'Death factor, species 1' ... 'Survival factor, species 2' 'Death factor, species 2'}, ... 'Unit', {'1/year' '1/year' '1/year' '1/year'}, ... 'Value', {1.8 0.8 1.2 0.8}, ... 'Minimum', {-Inf -Inf -Inf -Inf}, ... 'Maximum', {Inf Inf Inf Inf}, ... 'Fixed', {false false false false}); % Estimate all 4 parameters. InitialStates = struct('Name', {'Population, species 1' 'Population, species 2'}, ... 'Unit', {'Size (in thousands)' 'Size (in thousands)'}, ... 'Value', {0.2 1.8}, ... 'Minimum', {0 0}, ... 'Maximum', {Inf Inf}, ... 'Fixed', {false false}); % Estimate both initial states. Ts = 0; % Time-continuous system. nlgr = idnlgrey(FileName, Order, Parameters, InitialStates, Ts, ... 'Name', 'Two species competing for the same food', ... 'OutputName', {'Population, species 1' 'Population, species 2'}, ... 'OutputUnit', {'Size (in thousands)' 'Size (in thousands)'}, ... 'TimeUnit', 'year');
PRESENT コマンドを使用して、初期モデルの情報を表示できます。
present(nlgr);
nlgr =
Continuous-time nonlinear grey-box model defined by 'preys_m' (MATLAB file):
dx/dt = F(t, x(t), p1, ..., p4)
y(t) = H(t, x(t), p1, ..., p4) + e(t)
with 0 input(s), 2 state(s), 2 output(s), and 4 free parameter(s) (out of 4).
States: Initial value
x(1) Population, species 1(t) [Size (in t..] xinit@exp1 0.2 (estimated) in [0, Inf]
x(2) Population, species 2(t) [Size (in t..] xinit@exp1 1.8 (estimated) in [0, Inf]
Outputs:
y(1) Population, species 1(t) [Size (in thousands)]
y(2) Population, species 2(t) [Size (in thousands)]
Parameters: Value
p1 Survival factor, species 1 [1/year] 1.8 (estimated) in [-Inf, Inf]
p2 Death factor, species 1 [1/year] 0.8 (estimated) in [-Inf, Inf]
p3 Survival factor, species 2 [1/year] 1.2 (estimated) in [-Inf, Inf]
p4 Death factor, species 2 [1/year] 0.8 (estimated) in [-Inf, Inf]
Name: Two species competing for the same food
Status:
Created by direct construction or transformation. Not estimated.
More information in model's "Report" property.
Model Properties
A.2.入出力データ
次に、データ (ノイズで破損され、シミュレーションを実行したもの) を読み込んで、2 つの種が同じ食物で競合する状況を記述する IDDATA オブジェクトを作成します。このデータセットには 201 のデータ サンプルが含まれ、20 年分の進化を表します。
load('preydata'); z = iddata(y, [], 0.1, 'Name', 'Two species competing for the same food'); set(z, 'OutputName', {'Population, species 1', 'Population, species 2'}, ... 'Tstart', 0, 'TimeUnit', 'Year');
A.3.初期の 2 種モデルの性能
初期モデルのシミュレーションにより、実際の個体群ダイナミクスを表現できないことが明確にわかります。プロット図を参照してください。時系列タイプの IDNLGREY モデルでは、モデル出力は初期状態によって決定されます。
compare(z, nlgr, 1);

図 1: 初期の 2 種モデルの実際の出力とシミュレーションの出力の比較
A.4.パラメーター推定
初期モデルの低めの性能を解決するため、4 つの不明パラメーターと 2 つの初期状態を NLGREYEST を使用して推定します。推定オプションを NLGREYESTOPTIONS を使用して指定します。この例の場合、'Display' を 'on' に設定しますが、これは、推定の進捗状況についての情報が進行状況ウィンドウに表示されることを意味します。NLGREYESTOPTIONS を使用して、'GradientOptions'、'SearchMethod'、'MaxIterations'、'Tolerance'、'Display' などの基本的なアルゴリズム プロパティを指定できます。
opt = nlgreyestOptions;
opt.Display = 'on';
opt.SearchOptions.MaxIterations = 50;
nlgr = nlgreyest(z, nlgr, opt);A.5.推定された 2 種モデルの性能
パラメーターおよび初期状態の推定値は、実際の出力データの生成に使用された値と一致します。
disp(' True Estimated parameter vector');True Estimated parameter vector
ptrue = [2; 1; 1; 1];
fprintf(' %6.3f %6.3f\n', [ptrue'; getpvec(nlgr)']); 2.000 2.004
1.000 1.002
1.000 1.018
1.000 1.010
disp(' ');disp(' True Estimated initial states');True Estimated initial states
x0true = [0.1; 2]; fprintf(' %6.3f %6.3f\n', [x0true'; cell2mat(getinit(nlgr, 'Value'))']);
0.100 0.101
2.000 1.989
モデルの品質をさらに評価するため (また、初期モデルと比較した改善を示すため)、推定されたモデルもシミュレートします。シミュレーションの出力が、プロット ウィンドウで実際の出力と比較されます。示されるように、推定されたモデルは良好です。
compare(z, nlgr, 1);
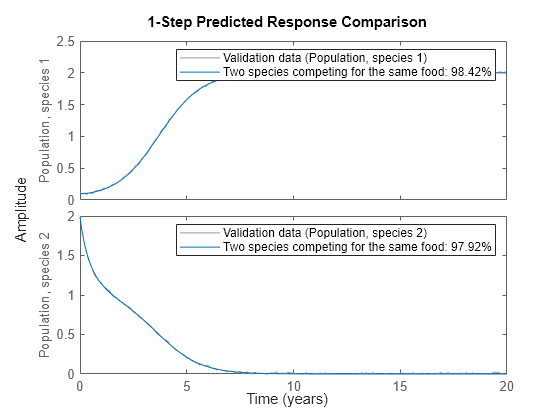
図 2: 推定された 2 種モデルの実際の出力とシミュレーションの出力の比較
PRESENT からは推定モデルの詳細情報が得られます。パラメーターの不確かさや、損失関数や赤池の FPE (最終予測誤差) 測定など、その他の推定関連の数量です。
present(nlgr);
nlgr =
Continuous-time nonlinear grey-box model defined by 'preys_m' (MATLAB file):
dx/dt = F(t, x(t), p1, ..., p4)
y(t) = H(t, x(t), p1, ..., p4) + e(t)
with 0 input(s), 2 state(s), 2 output(s), and 4 free parameter(s) (out of 4).
States: Initial value
x(1) Population, species 1(t) [Size (in t..] xinit@exp1 0.100729 (estimated) in [0, Inf]
x(2) Population, species 2(t) [Size (in t..] xinit@exp1 1.98855 (estimated) in [0, Inf]
Outputs:
y(1) Population, species 1(t) [Size (in thousands)]
y(2) Population, species 2(t) [Size (in thousands)]
Parameters: ValueStandard Deviation
p1 Survival factor, species 1 [1/year] 2.00429 0.00971109 (estimated) in [-Inf, Inf]
p2 Death factor, species 1 [1/year] 1.00235 0.00501783 (estimated) in [-Inf, Inf]
p3 Survival factor, species 2 [1/year] 1.01779 0.0229598 (estimated) in [-Inf, Inf]
p4 Death factor, species 2 [1/year] 1.0102 0.0163506 (estimated) in [-Inf, Inf]
Name: Two species competing for the same food
Status:
Termination condition: Near (local) minimum, (norm(g) < tol)..
Number of iterations: 5, Number of function evaluations: 6
Estimated using Solver: ode45; Search: lsqnonlin on time domain data "Two species competing for the same food".
Fit to estimation data: [98.42;97.92]%
FPE: 7.747e-09, MSE: 0.0001743
More information in model's "Report" property.
Model Properties
B.1.従来の捕食系
ここで、最初の種が 2 番目の種を捕食すると仮定します。種 1 の食物の取得可能性は、x2(t) (種 2 の個体数) に比例し、種 1 の死亡率は x2(t) が増加すると減少します。この事実は、簡単な式で表現されます。
u1(x1(t), x2(t)) = g1 - a1*x2(t)
ここで、g1 と a1 は不明パラメーターです。同様に、種 2 の死亡率は、最初の種の個体数が増加すると、次のように増加します。
u2(x1(t), x2(t)) = g2 + a2*x1(t)
ここで、g2 と a2 も 2 つの不明パラメーターです。上記で仮定した線形出生率を使用して、次の状態空間構造が得られます。
d
-- x1(t) = (l1-g1)*x1(t) + a1*x2(t)*x1(t)
dt
d
-- x2(t) = (l2-g2)*x2(t) - a2*x1(t)*x2(t)
dt
前の個体群の例と同様に、ここでも 6 つのパラメーターを個別に特定することはできません。上記の場合と同じ再パラメーター化の p1 = l1-g1、p2 = a1、p3 = l2-g2、p4 = a2 によって、次のモデル構造が得られます。
d
-- x1(t) = p1*x1(t) + p2*x2(t)*x1(t)
dt
d
-- x2(t) = p3*x2(t) - p4*x1(t)*x2(t)
dt
y1(t) = x1(t)
y2(t) = x2(t)
これは推定の観点からはより適しています。
今度は、この情報を predprey1_c.c という C MEX ファイルに入力します。このモデル ファイルは標準の IDNLGREY C MEX ファイルとして構成されており (「IDNLGREY モデル ファイルの作成」の例または idnlgreydemo2.m を参照してください)、状態更新関数および出力更新関数の compute_dx と compute_y は次のようになっています。
void compute_dx(double *dx, double t, double *x, double **p, const mxArray *auxvar) { /* Retrieve model parameters. */ double *p1, *p2, *p3, *p4; p1 = p[0]; /* Survival factor, predators. */ p2 = p[1]; /* Death factor, predators. */ p3 = p[2]; /* Survival factor, preys. */ p4 = p[3]; /* Death factor, preys. */ /* x[0]: Predator species. */ /* x[1]: Prey species. */ dx[0] = p1[0]*x[0]+p2[0]*x[1]*x[0]; dx[1] = p3[0]*x[1]-p4[0]*x[0]*x[1]; } /* Output equations. */ void compute_y(double *y, double t, double *x, double **p, const mxArray *auxvar) { /* y[0]: Predator species. */ /* y[1]: Prey species. */ y[0] = x[0]; y[1] = x[1]; }
モデルは時系列タイプなので、ompute_dx にも compute_y にも入力引数リストに u はありません。実際、predprey1_c.c のメイン インターフェイス関数は、IDNLGREY メソッドが predprey1_c に空の u ([]) が常に渡される場合でも、u を宣言しません。
次に、コンパイルした C MEX ファイルと初期パラメーター ベクトル、適切な初期状態、一部の管理情報を入力引数として IDNLGREY オブジェクト コンストラクターに指定します。
FileName = 'predprey1_c'; % File describing the model structure. Order = [2 0 2]; % Model orders [ny nu nx]. Parameters = struct('Name', {'Survival factor, predators' 'Death factor, predators' ... 'Survival factor, preys' 'Death factor, preys'}, ... 'Unit', {'1/year' '1/year' '1/year' '1/year'}, ... 'Value', {-1.1 0.9 1.1 0.9}, ... 'Minimum', {-Inf -Inf -Inf -Inf}, ... 'Maximum', {Inf Inf Inf Inf}, ... 'Fixed', {false false false false}); % Estimate all 4 parameters. InitialStates = struct('Name', {'Population, predators' 'Population, preys'}, ... 'Unit', {'Size (in thousands)' 'Size (in thousands)'}, ... 'Value', {1.8 1.8}, ... 'Minimum', {0 0}, ... 'Maximum', {Inf Inf}, ... 'Fixed', {false false}); % Estimate both initial states. Ts = 0; % Time-continuous system. nlgr = idnlgrey(FileName, Order, Parameters, InitialStates, Ts, ... 'Name', 'Classical 1 predator - 1 prey system', ... 'OutputName', {'Population, predators', 'Population, preys'}, ... 'OutputUnit', {'Size (in thousands)' 'Size (in thousands)'}, ... 'TimeUnit', 'year');
次に、捕食者モデルを PRESENT コマンドでテキストとして表示します。
present(nlgr);
nlgr =
Continuous-time nonlinear grey-box model defined by 'predprey1_c' (MEX-file):
dx/dt = F(t, x(t), p1, ..., p4)
y(t) = H(t, x(t), p1, ..., p4) + e(t)
with 0 input(s), 2 state(s), 2 output(s), and 4 free parameter(s) (out of 4).
States: Initial value
x(1) Population, predators(t) [Size (in t..] xinit@exp1 1.8 (estimated) in [0, Inf]
x(2) Population, preys(t) [Size (in t..] xinit@exp1 1.8 (estimated) in [0, Inf]
Outputs:
y(1) Population, predators(t) [Size (in thousands)]
y(2) Population, preys(t) [Size (in thousands)]
Parameters: Value
p1 Survival factor, predators [1/year] -1.1 (estimated) in [-Inf, Inf]
p2 Death factor, predators [1/year] 0.9 (estimated) in [-Inf, Inf]
p3 Survival factor, preys [1/year] 1.1 (estimated) in [-Inf, Inf]
p4 Death factor, preys [1/year] 0.9 (estimated) in [-Inf, Inf]
Name: Classical 1 predator - 1 prey system
Status:
Created by direct construction or transformation. Not estimated.
More information in model's "Report" property.
Model Properties
B.2.入出力データ
次のステップでは、データ (ノイズで破損され、シミュレーションを実行したもの) を読み込んで、この捕食者状況を記述する IDDATA オブジェクトを作成します。このデータセットには 201 のデータ サンプルも含まれ、20 年分の進化を表します。
load('predprey1data'); z = iddata(y, [], 0.1, 'Name', 'Classical 1 predator - 1 prey system'); set(z, 'OutputName', {'Population, predators', 'Population, preys'}, ... 'Tstart', 0, 'TimeUnit', 'Year');
B.3.初期の古典的な捕食モデルの性能
初期モデルのシミュレーションにより、実際の個体群ダイナミクスを正確には処理できないことがわかります。プロット ウィンドウを参照します。
compare(z, nlgr, 1);

図 3: 初期の古典的な捕食モデルの実際の出力とシミュレーションの出力の比較
B.4.パラメーター推定
初期モデルの性能を改善するため、4 つの不明なパラメーターと 2 つの初期状態を NLGREYEST を使用して推定します。
nlgr = nlgreyest(z, nlgr, nlgreyestOptions('Display', 'on'));
B.5.推定された古典的な捕食モデルの性能
パラメーターおよび初期状態の推定値は、実際の出力データの生成に使用された値と非常に近いものです。
disp(' True Estimated parameter vector');True Estimated parameter vector
ptrue = [-1; 1; 1; 1];
fprintf(' %6.3f %6.3f\n', [ptrue'; getpvec(nlgr)']); -1.000 -1.000
1.000 1.000
1.000 1.000
1.000 0.999
disp(' ');disp(' True Estimated initial states');True Estimated initial states
x0true = [2; 2]; fprintf(' %6.3f %6.3f\n', [x0true'; cell2mat(getinit(nlgr, 'Value'))']);
2.000 2.002
2.000 2.000
モデルの品質をさらに評価するため (また、初期モデルと比較した改善を示すため)、推定されたモデルもシミュレートします。シミュレーションの出力が、プロット ウィンドウで実際の出力と比較されます。ここでもわかるように、推定されたモデルは良好です。
compare(z, nlgr, 1);

図 4: 推定された古典的な捕食モデルの実際の出力とシミュレーションの出力の比較
予期したとおり、PE から返される予測誤差は小さく、ランダムです。
pe(z, nlgr);
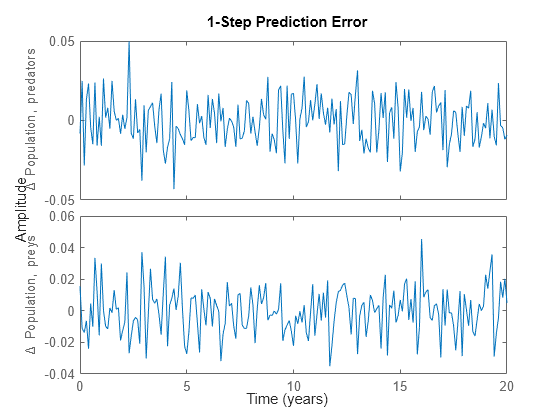
図 5: IDNLGREY の推定された古典的な捕食モデルで取得した予測誤差
C.1.被捕食者の群れがある捕食系
最後の個体群の調査も、捕食者 1 つと被捕食者 1 のシステムを使用しますが、ここでは群れをなすことによって捕食者が減少することを表す項 -p5*x2(t)^2 r が導入されているという違いがあります。以前のサンプルを再パラメーター化したモデル構造は、この群による項が付加されています。
d
-- x1(t) = p1*x1(t) + p2*x2(t)*x1(t)
dt
d
-- x2(t) = p3*x2(t) - p4*x1(t)*x2(t) - p5*x2(t)^2
dt
y1(t) = x1(t)
y2(t) = x2(t)
これらの方程式の解釈は基本的に上記と同一ですが、捕食者がいない場合は被捕食者の個体数の増加は抑制される点が異なります。
新しいモデル化状況が C MEX ファイル predprey2_c.c で反映されます。これは predprey1_c.c とほぼ同一です。モデル パラメーターの数に関連する変更 (4 から 5 に変更) を除き、主な変更は状態更新関数 compute_dx についてです。
/* State equations. */ void compute_dx(double *dx, double t, double *x, double **p, const mxArray *auxvar) { /* Retrieve model parameters. */ double *p1, *p2, *p3, *p4, *p5; p1 = p[0]; /* Survival factor, predators. */ p2 = p[1]; /* Death factor, predators. */ p3 = p[2]; /* Survival factor, preys. */ p4 = p[3]; /* Death factor, preys. */ p5 = p[4]; /* Crowding factor, preys. */ /* x[0]: Predator species. */ /* x[1]: Prey species. */ dx[0] = p1[0]*x[0]+p2[0]*x[1]*x[0]; dx[1] = p3[0]*x[1]-p4[0]*x[0]*x[1]-p5[0]*pow(x[1],2); }
追加された減少項は p5[0]*pow(x[1],2) として計算されます。べき乗関数 pow(., .) は C ライブラリの math.h で定義されます。これはモデル ファイルの先頭でステートメント #include "math.h" を使用して指定しなければなりません (predprey1_c.c の場合は、標準 C 数学関数のみがあるために必須ではありません)。
次に、コンパイルした C MEX ファイルと初期パラメーター ベクトル、適切な初期状態、一部の管理情報を入力引数として IDNLGREY オブジェクト コンストラクターに指定します。
FileName = 'predprey2_c'; % File describing the model structure. Order = [2 0 2]; % Model orders [ny nu nx]. Parameters = struct('Name', {'Survival factor, predators' 'Death factor, predators' ... 'Survival factor, preys' 'Death factor, preys' ... 'Crowding factor, preys'}, ... 'Unit', {'1/year' '1/year' '1/year' '1/year' '1/year'}, ... 'Value', {-1.1 0.9 1.1 0.9 0.2}, ... 'Minimum', {-Inf -Inf -Inf -Inf -Inf}, ... 'Maximum', {Inf Inf Inf Inf Inf}, ... 'Fixed', {false false false false false}); % Estimate all 5 parameters. InitialStates = struct('Name', {'Population, predators' 'Population, preys'}, ... 'Unit', {'Size (in thousands)' 'Size (in thousands)'}, ... 'Value', {1.8 1.8}, ... 'Minimum', {0 0}, ... 'Maximum', {Inf Inf}, ... 'Fixed', {false false}); % Estimate both initial states. Ts = 0; % Time-continuous system. nlgr = idnlgrey(FileName, Order, Parameters, InitialStates, Ts, ... 'Name', '1 predator - 1 prey system exhibiting crowding', ... 'OutputName', {'Population, predators', 'Population, preys'}, ... 'OutputUnit', {'Size (in thousands)' 'Size (in thousands)'}, ... 'TimeUnit', 'year');
モデル オブジェクトの名前 (nlgr) を入力すると、モデルの基本情報がコマンド ウィンドウに表示されます。以前と同様に、present(nlgr) からはモデルの総合的な概要が得られます。
nlgr
nlgr =
Continuous-time nonlinear grey-box model defined by 'predprey2_c' (MEX-file):
dx/dt = F(t, x(t), p1, ..., p5)
y(t) = H(t, x(t), p1, ..., p5) + e(t)
with 0 input(s), 2 state(s), 2 output(s), and 5 free parameter(s) (out of 5).
Name: 1 predator - 1 prey system exhibiting crowding
Status:
Created by direct construction or transformation. Not estimated.
Model Properties
C.2.入出力データ
次に、データ (ノイズで破損され、シミュレーションを実行したもの) を読み込んで、この捕食者状況の密生タイプを記述する IDDATA オブジェクトを作成します。このデータセットには 201 のデータ サンプルが含まれ、20 年分の進化を表します。
load('predprey2data'); z = iddata(y, [], 0.1, 'Name', '1 predator - 1 prey system exhibiting crowding'); set(z, 'OutputName', {'Population, predators', 'Population, preys'}, ... 'Tstart', 0, 'TimeUnit', 'Year');
C.3.被捕食者の群れがある初期の捕食系モデルの性能
初期モデルのシミュレーションにより、実際の個体群ダイナミクスを表現できないことが明確にわかります。図を参照してください。
clf compare(z, nlgr, 1);
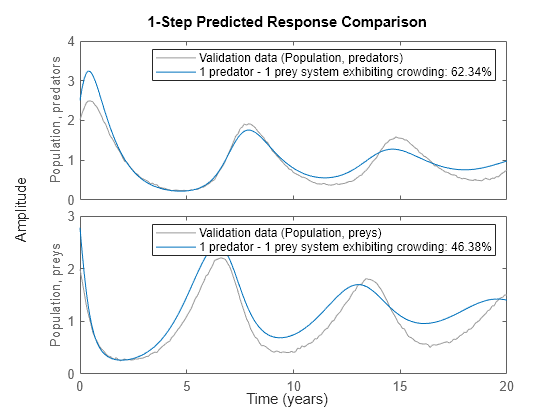
図 6: 初期の被捕食者の群れがある捕食者モデルの実際の出力とシミュレーションの出力の比較
C.4.パラメーター推定
初期モデルの性能の低さを改良するため、5 つの不明パラメーターと 2 つの初期状態を推定します。
nlgr = nlgreyest(z, nlgr, nlgreyestOptions('Display', 'on'));
C.5.被捕食者の群れがある推定された捕食系モデルの性能
パラメーターおよび初期状態の推定値は、実際の出力データの生成に使用された値と非常に近いものです。
disp(' True Estimated parameter vector');True Estimated parameter vector
ptrue = [-1; 1; 1; 1; 0.1];
fprintf(' %6.3f %6.3f\n', [ptrue'; getpvec(nlgr)']); -1.000 -1.000
1.000 1.001
1.000 1.002
1.000 1.002
0.100 0.101
disp(' ');disp(' True Estimated initial states');True Estimated initial states
x0true = [2; 2]; fprintf(' %6.3f %6.3f\n', [x0true'; cell2mat(getinit(nlgr, 'Value'))']);
2.000 2.003
2.000 2.002
モデルの品質をさらに評価するため (また、初期モデルと比較した改善を示すため)、推定されたモデルもシミュレートします。シミュレーションの出力が、プロット ウィンドウで実際の出力と比較されます。ここでもわかるように、推定されたモデルは良好です。
compare(z, nlgr, 1);
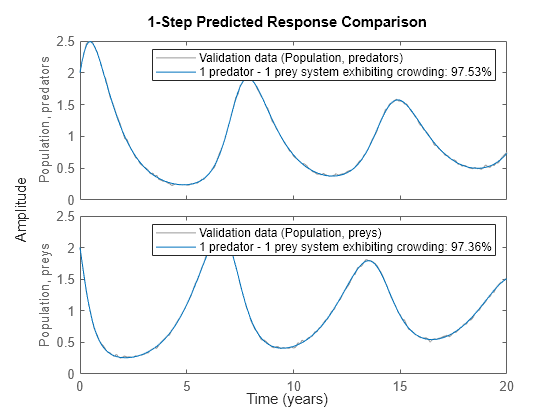
図 7: 推定された被捕食者の群れがある捕食者モデルの実際の出力とシミュレーションの出力の比較
3 番目の個体群の例の最後として、PRESENT で返されるモデル情報を示します。
present(nlgr);
nlgr =
Continuous-time nonlinear grey-box model defined by 'predprey2_c' (MEX-file):
dx/dt = F(t, x(t), p1, ..., p5)
y(t) = H(t, x(t), p1, ..., p5) + e(t)
with 0 input(s), 2 state(s), 2 output(s), and 5 free parameter(s) (out of 5).
States: Initial value
x(1) Population, predators(t) [Size (in t..] xinit@exp1 2.00281 (estimated) in [0, Inf]
x(2) Population, preys(t) [Size (in t..] xinit@exp1 2.00224 (estimated) in [0, Inf]
Outputs:
y(1) Population, predators(t) [Size (in thousands)]
y(2) Population, preys(t) [Size (in thousands)]
Parameters: Value Standard Deviation
p1 Survival factor, predators [1/year] -0.999914 0.00280581 (estimated) in [-Inf, Inf]
p2 Death factor, predators [1/year] 1.00058 0.00276684 (estimated) in [-Inf, Inf]
p3 Survival factor, preys [1/year] 1.0019 0.00272154 (estimated) in [-Inf, Inf]
p4 Death factor, preys [1/year] 1.00224 0.00268423 (estimated) in [-Inf, Inf]
p5 Crowding factor, preys [1/year] 0.101331 0.0005023 (estimated) in [-Inf, Inf]
Name: 1 predator - 1 prey system exhibiting crowding
Status:
Termination condition: Change in cost was less than the specified tolerance..
Number of iterations: 8, Number of function evaluations: 9
Estimated using Solver: ode45; Search: lsqnonlin on time domain data "1 predator - 1 prey system exhibiting crowding".
Fit to estimation data: [97.53;97.36]%
FPE: 4.327e-08, MSE: 0.0004023
More information in model's "Report" property.
Model Properties
まとめ
この例では、MATLAB および MEX モデル ファイルに基づいて IDNLGREY 時系列モデリングを実行する方法を説明しました。