このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
空力体のモデル化
この例は、大規模で複雑な非線形システムのグレーボックス モデリングを示しています。目的は、IDNLGREY モデルを使用して多数の入力 (10) と出力 (5) をもつシステムで多数のパラメーター (16) を推定できることを示すことです。システムは空力体です。速度 (並進および角度) と制御面に関連するさまざまな角度の測定を使用して、空力体の加速度と速度を予測するモデルを作成します。
入出力データ
測定された速度、角度、動的圧力を、aerodata.mat というデータ ファイルから読み込みます。
load('aerodata');このファイルには、変数 u と y の 501 件のサンプルがある、等間隔でサンプリングされたデータセットが含まれています。サンプル時間は 0.02 秒です。このデータセットは、さらに詳細な別の空力体モデルから生成されています。
次に、IDDATA オブジェクトを作成してデータを表現し、格納します。
z = iddata(y, u, 0.02, 'Name', 'Data'); z.InputName = {'Aileron angle' 'Elevator angle' ... 'Rudder angle' 'Dynamic pressure' ... 'Velocity' ... 'Measured angular velocity around x-axis' ... 'Measured angular velocity around y-axis' ... 'Measured angular velocity around z-axis' ... 'Measured angle of attack' ... 'Measured angle of sideslip'}; z.InputUnit = {'rad' 'rad' 'rad' 'kg/(m*s^2)' 'm/s' ... 'rad/s' 'rad/s' 'rad/s' 'rad' 'rad'}; z.OutputName = {'V(x)' ... % Angular velocity around x-axis 'V(y)' ... % Angular velocity around y-axis 'V(z)' ... % Angular velocity around z-axis 'Accel.(y)' ... % Acceleration in y-direction 'Accel.(z)' ... % Acceleration in z-direction }; z.OutputUnit = {'rad/s' 'rad/s' 'rad/s' 'm/s^2' 'm/s^2'}; z.Tstart = 0; z.TimeUnit = 's';
入力データを表示します。
figure('Name', [z.Name ': input data'],... 'DefaultAxesTitleFontSizeMultiplier',1,... 'DefaultAxesTitleFontWeight','normal',... 'Position',[50, 50, 850, 620]); for i = 1:z.Nu subplot(z.Nu/2, 2, i); plot(z.SamplingInstants, z.InputData(:,i)); title(['Input #' num2str(i) ': ' z.InputName{i}],'FontWeight','normal'); xlabel(''); axis tight; if (i > z.Nu-2) xlabel([z.Domain ' (' z.TimeUnit ')']); end end
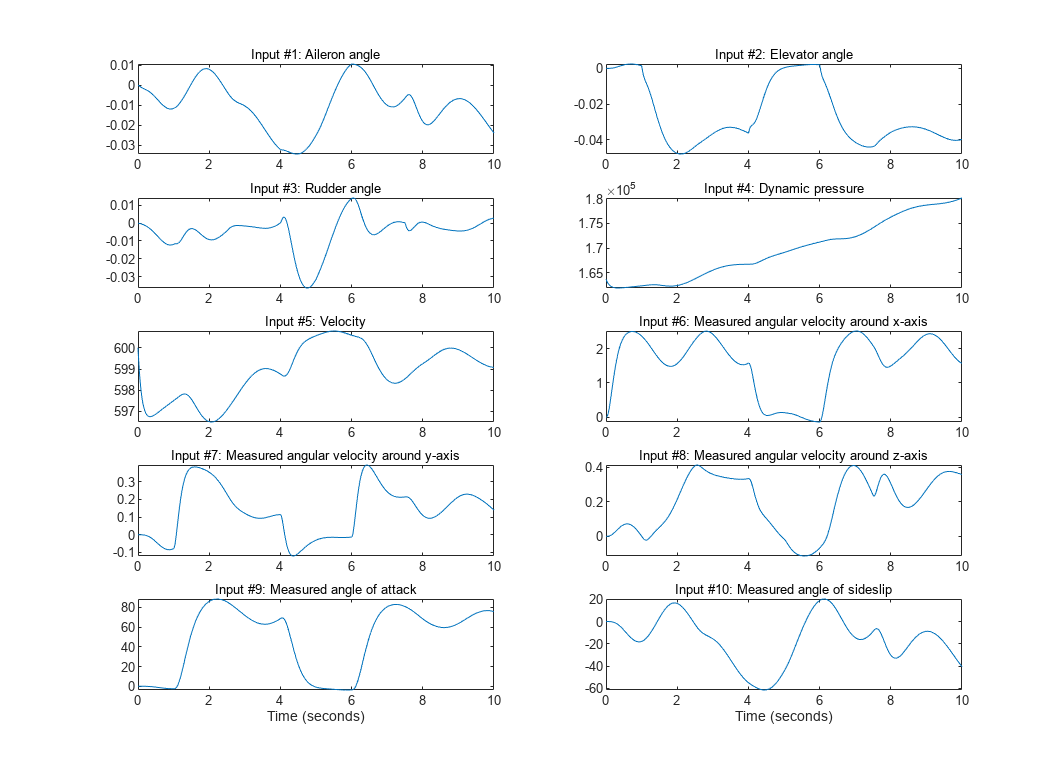
図 1: 入力信号
出力データを表示します。
figure('Name', [z.Name ': output data']); h_gcf = gcf; Pos = h_gcf.Position; h_gcf.Position = [Pos(1), Pos(2)-Pos(4)/2, Pos(3), Pos(4)*1.5]; for i = 1:z.Ny subplot(z.Ny, 1, i); plot(z.SamplingInstants, z.OutputData(:,i)); title(['Output #' num2str(i) ': ' z.OutputName{i}]); xlabel(''); axis tight; end xlabel([z.Domain ' (' z.TimeUnit ')']);

図 2: 出力信号
一部の出力の測定変数が入力ベクトルにあるのは、奇妙です。ただし、データの生成に使用されたモデルには、複数の積分器が含まれており、シミュレーションの動作が不安定になることがよくあります。これを防止するため、一部の出力信号の測定を非線形オブザーバーからフィードバックします。これらはデータセット z の入力 6 ~ 8 に該当します。したがって、閉ループで動作するシステムであり、モデル化作業の目標は、現在および過去の動作の測定値を使用してこれらの出力の「将来」の値を予測することです。
システムのモデル化
対象のダイナミクスをモデル化するため、IDNLGREY モデル オブジェクトを使用してシステムの状態空間構造を表現します。ニュートンの力とモーメントの基本法則 (釣合方程式) を使用して合理的な構造が得られます。モデル構造を完全に記述するため、基本的な空力関係 (構成関係) も使用されます。
C MEX ファイル aero_c.c は、状態方程式および出力方程式と初期条件を使用して、次のようにシステムを記述します。運動方程式の導出の詳細を省き、最終的な状態および出力方程式のみを表示します。また、構造は非線形で、非常に複雑であることがわかります。
/* State equations. */
void compute_dx(double *dx, double *x, double *u, double **p)
{
/* Retrieve model parameters. */
double *F, *M, *C, *d, *A, *I, *m, *K;
F = p[0]; /* Aerodynamic force coefficient. */
M = p[1]; /* Aerodynamic momentum coefficient. */
C = p[2]; /* Aerodynamic compensation factor. */
d = p[3]; /* Body diameter. */
A = p[4]; /* Body reference area. */
I = p[5]; /* Moment of inertia, x-y-z. */
m = p[6]; /* Mass. */
K = p[7]; /* Feedback gain. */
/* x[0]: Angular velocity around x-axis. */
/* x[1]: Angular velocity around y-axis. */
/* x[2]: Angular velocity around z-axis. */
/* x[3]: Angle of attack. */
/* x[4]: Angle of sideslip. */
dx[0] = 1/I[0]*(d[0]*A[0]*(M[0]*x[4]+0.5*M[1]*d[0]*x[0]/u[4]+M[2]*u[0])*u[3]-(I[2]-I[1])*x[1]*x[2])+K[0]*(u[5]-x[0]);
dx[1] = 1/I[1]*(d[0]*A[0]*(M[3]*x[3]+0.5*M[4]*d[0]*x[1]/u[4]+M[5]*u[1])*u[3]-(I[0]-I[2])*x[0]*x[2])+K[0]*(u[6]-x[1]);
dx[2] = 1/I[2]*(d[0]*A[0]*(M[6]*x[4]+M[7]*x[3]*x[4]+0.5*M[8]*d[0]*x[2]/u[4]+M[9]*u[0]+M[10]*u[2])*u[3]-(I[1]-I[0])*x[0]*x[1])+K[0]*(u[7]-x[2]);
dx[3] = (-A[0]*u[3]*(F[2]*x[3]+F[3]*u[1]))/(m[0]*u[4])-x[0]*x[4]+x[1]+K[0]*(u[8]/u[4]-x[3])+C[0]*pow(x[4],2);
dx[4] = (-A[0]*u[3]*(F[0]*x[4]+F[1]*u[2]))/(m[0]*u[4])-x[2]+x[0]*x[3]+K[0]*(u[9]/u[4]-x[4]);
}
/* Output equations. */
void compute_y(double *y, double *x, double *u, double **p)
{
/* Retrieve model parameters. */
double *F, *A, *m;
F = p[0]; /* Aerodynamic force coefficient. */
A = p[4]; /* Body reference area. */
m = p[6]; /* Mass. */
/* y[0]: Angular velocity around x-axis. */
/* y[1]: Angular velocity around y-axis. */
/* y[2]: Angular velocity around z-axis. */
/* y[3]: Acceleration in y-direction. */
/* y[4]: Acceleration in z-direction. */
y[0] = x[0];
y[1] = x[1];
y[2] = x[2];
y[3] = -A[0]*u[3]*(F[0]*x[4]+F[1]*u[2])/m[0];
y[4] = -A[0]*u[3]*(F[2]*x[3]+F[3]*u[1])/m[0];
}
23 個のパラメーターの開始値を指定する必要もあります。一部のパラメーター (空力係数、空力モーメント係数、慣性モーメント係数) を 8 つの異なるパラメーター オブジェクトとして指定します。初期パラメーター値は、一部は物理的推論によって、一部は定量的推定によって得られます。最後の 4 つのパラメーター (A、I、m、K) はある程度一定で、これらのパラメーターを固定することで、パラメーター オブジェクト F、M、C、d に分散された 16 の自由パラメーターでモデル構造を得られます。
Parameters = struct('Name', ... {'Aerodynamic force coefficient' ... % F, 4-by-1 vector. 'Aerodynamic momentum coefficient' ... % M, 11-by-1 vector. 'Aerodynamic compensation factor' ... % C, scalar. 'Body diameter' ... % d, scalar. 'Body reference area' ... % A, scalar. 'Moment of inertia, x-y-z' ... % I, 3-by-1 vector. 'Mass' ... % m, scalar. 'Feedback gain'}, ... % K, scalar. 'Unit', ... {'1/(rad*m^2), 1/(rad*m^2), 1/(rad*m^2), 1/(rad*m^2)' ... ['1/rad, 1/(s*rad), 1/rad, 1/rad, ' ... '1/(s*rad), 1/rad, 1/rad, 1/rad^2, ' ... '1/(s*rad), 1/rad, 1/rad'] ... '1/(s*rad)' 'm' 'm^2' ... 'kg*m^2, kg*m^2,kg*m^2' 'kg' '-'}, ... 'Value', ... {[20.0; -6.0; 35.0; 13.0] ... [-1.0; 15; 3.0; -16.0; -1800; -50; 23.0; -200; -2000; -17.0; -50.0] ... -5.0, 0.17, 0.0227 ... [0.5; 110; 110] 107 6}, ... 'Minimum',... {-Inf(4, 1) -Inf(11, 1) -Inf -Inf -Inf -Inf(3, 1) -Inf -Inf}, ... % Ignore constraints. 'Maximum', ... {Inf(4, 1) Inf(11, 1) Inf Inf Inf Inf(3, 1) Inf Inf}, ... % Ignore constraints. 'Fixed', ... {false(4, 1) false(11, 1) false true true true(3, 1) true true});
同じ方法で、モデル構造の 5 つの状態も定義します。
InitialStates = struct('Name', {'Angular velocity around x-axis' ... 'Angular velocity around y-axis' ... 'Angular velocity around z-axis' ... 'Angle of attack' 'Angle of sideslip'}, ... 'Unit', {'rad/s' 'rad/s' 'rad/s' 'rad' 'rad'}, ... 'Value', {0 0 0 0 0}, ... 'Minimum', {-Inf -Inf -Inf -Inf -Inf},... % Ignore constraints. 'Maximum', {Inf Inf Inf Inf Inf},... % Ignore constraints. 'Fixed', {true true true true true});
次数、パラメーター、初期状態データを含むモデル ファイルを使用して、システムを記述する IDNLGREY オブジェクトを作成します。
FileName = 'aero_c'; % File describing the model structure. Order = [5 10 5]; % Model orders [ny nu nx]. Ts = 0; % Time-continuous system. nlgr = idnlgrey(FileName, Order, Parameters, InitialStates, Ts, ... 'Name', 'Model', 'TimeUnit', 's');
次に、IDDATA オブジェクトからのデータを使用して、システムの入出力信号を指定します。
nlgr.InputName = z.InputName; nlgr.InputUnit = z.InputUnit; nlgr.OutputName = z.OutputName; nlgr.OutputUnit = z.OutputUnit;
10 個の入力信号、5 個の状態、5 個の出力信号をもつ、IDNLGREY オブジェクトが得られます。前述のように、モデルには 23 個のパラメーターがあり、そのうち 7 個は固定され、16 個は自由です。
nlgr
nlgr =
Continuous-time nonlinear grey-box model defined by 'aero_c' (MEX-file):
dx/dt = F(t, u(t), x(t), p1, ..., p8)
y(t) = H(t, u(t), x(t), p1, ..., p8) + e(t)
with 10 input(s), 5 state(s), 5 output(s), and 16 free parameter(s) (out of 23).
Name: Model
Status:
Created by direct construction or transformation. Not estimated.
Model Properties
初期モデルの性能
16 個の自由パラメーターを推定する前に、初期パラメーター ベクトルを使用してシステムを推定します。シミュレーションによって、初期モデルの性質についての有益な情報が得られます。
clf
compare(z, nlgr); % simulate the model and compare the response to measured values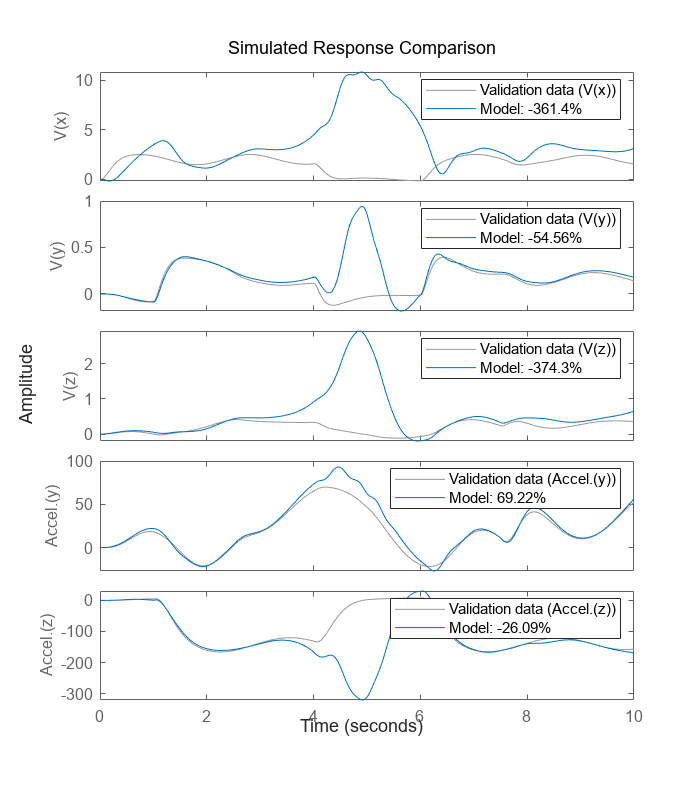
図 3: 初期モデルの測定された出力とシミュレーションの出力の比較
プロットから、測定された信号とシミュレーションの信号が、タイム スパン 4 ~ 6 秒を除いて、相互に近いことがわかります。この事実は、予測誤差のプロットで明らかです。
figure; h_gcf = gcf; Pos = h_gcf.Position; h_gcf.Position = [Pos(1), Pos(2)-Pos(4)/2, Pos(3), Pos(4)*1.5]; pe(z, nlgr);
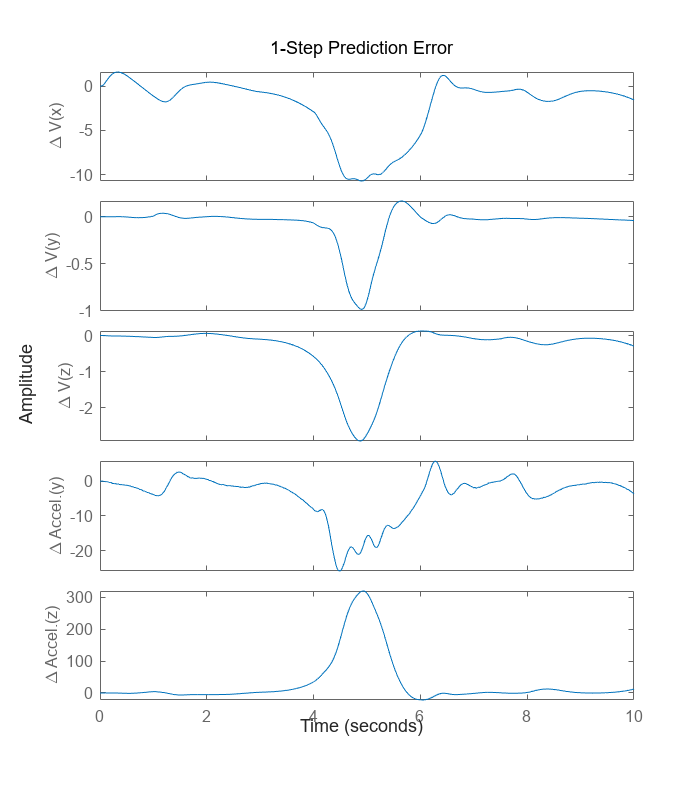
図 4: 初期モデルの予測誤差
パラメーター推定
上記で定義した初期モデルから、パラメーター推定を開始できます。次に、16 個の自由パラメーターの予測誤差推定を計算します。これらの計算には時間がかかります。
duration = clock; nlgr = nlgreyest(z, nlgr, nlgreyestOptions('Display', 'on')); duration = etime(clock, duration);
推定された空力体モデルの性能
使用するコンピューターで、パラメーターの推定を完了するには次の時間がかかりました。
disp(['Estimation time : ' num2str(duration, 4) ' seconds']);
Estimation time : 13.12 seconds
disp(['Time per iteration: ' num2str(duration/nlgr.Report.Termination.Iterations, 4) ' seconds.']);
Time per iteration: 0.6249 seconds.
推定されたモデルの性質を評価し、初期モデルと比較した改善を示すため、推定されたモデルをシミュレートして、測定された出力とシミュレーションの出力を比較します。
clf compare(z, nlgr);
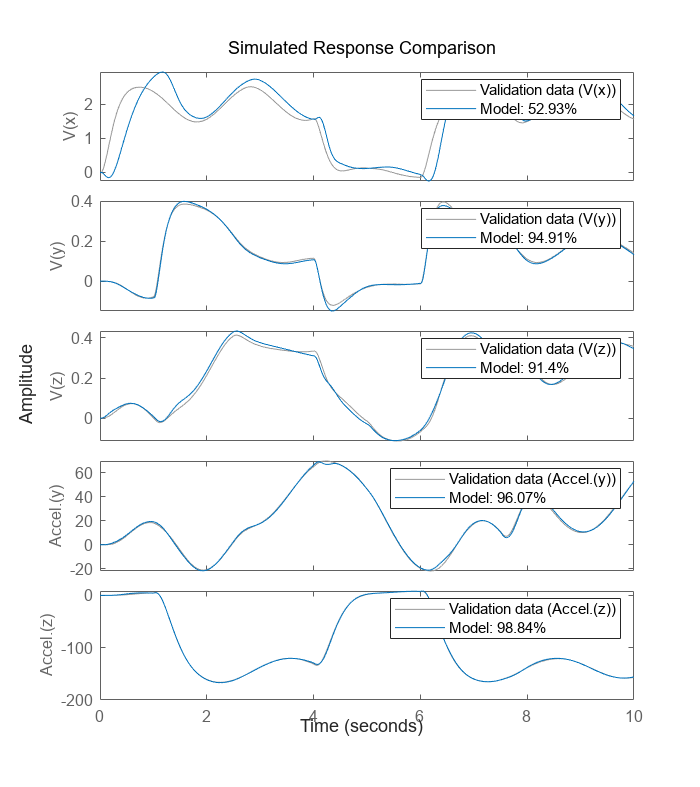
図 5: 推定されたモデルの測定された出力とシミュレーションの出力の比較
図から、初期モデルで得られたシミュレーション結果との比較による改善が明確にわかります。タイム スパン 4 ~ 6 秒のシステム ダイナミクスは、これまでよりも高精度で取得されています。これは予測誤差によって最も正確に示されています。
figure; h_gcf = gcf; Pos = h_gcf.Position; h_gcf.Position = [Pos(1), Pos(2)-Pos(4)/2, Pos(3), Pos(4)*1.5]; pe(z, nlgr);
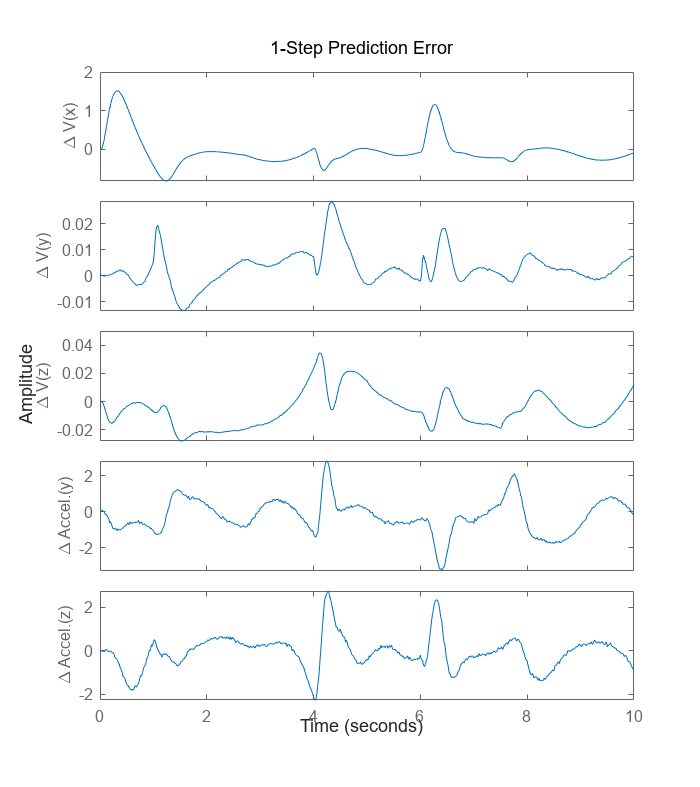
図 6: 推定されたモデルの予測誤差
ケース スタディの最後に、モデルと推定された不確かさを示します。
present(nlgr);
nlgr =
Continuous-time nonlinear grey-box model defined by 'aero_c' (MEX-file):
dx/dt = F(t, u(t), x(t), p1, ..., p8)
y(t) = H(t, u(t), x(t), p1, ..., p8) + e(t)
with 10 input(s), 5 state(s), 5 output(s), and 16 free parameter(s) (out of 23).
Inputs:
u(1) Aileron angle(t) [rad]
u(2) Elevator angle(t) [rad]
u(3) Rudder angle(t) [rad]
u(4) Dynamic pressure(t) [kg/(m*s^2)]
u(5) Velocity(t) [m/s]
u(6) Measured angular velocity around x-axis(t) [rad/s]
u(7) Measured angular velocity around y-axis(t) [rad/s]
u(8) Measured angular velocity around z-axis(t) [rad/s]
u(9) Measured angle of attack(t) [rad]
u(10) Measured angle of sideslip(t) [rad]
States: Initial value
x(1) Angular velocity around x-axis(t) [rad/s] xinit@exp1 0 (fixed) in [-Inf, Inf]
x(2) Angular velocity around y-axis(t) [rad/s] xinit@exp1 0 (fixed) in [-Inf, Inf]
x(3) Angular velocity around z-axis(t) [rad/s] xinit@exp1 0 (fixed) in [-Inf, Inf]
x(4) Angle of attack(t) [rad] xinit@exp1 0 (fixed) in [-Inf, Inf]
x(5) Angle of sideslip(t) [rad] xinit@exp1 0 (fixed) in [-Inf, Inf]
Outputs:
y(1) V(x)(t) [rad/s]
y(2) V(y)(t) [rad/s]
y(3) V(z)(t) [rad/s]
y(4) Accel.(y)(t) [m/s^2]
y(5) Accel.(z)(t) [m/s^2]
Parameters: Value Standard Deviation
p1(1) Aerodynamic force coefficient [1/(rad*m^2..] 21.2863 0.339394 (estimated) in [-Inf, Inf]
p1(2) -7.62502 0.180264 (estimated) in [-Inf, Inf]
p1(3) 35.0799 0.657227 (estimated) in [-Inf, Inf]
p1(4) 8.58246 1.08611 (estimated) in [-Inf, Inf]
p2(1) Aerodynamic momentum coefficient [1/rad, 1/(..] -1.0476 0.0733533 (estimated) in [-Inf, Inf]
p2(2) 15.6854 0.883102 (estimated) in [-Inf, Inf]
p2(3) 3.00613 0.199227 (estimated) in [-Inf, Inf]
p2(4) -17.7963 0.324639 (estimated) in [-Inf, Inf]
p2(5) -1060.91 224.269 (estimated) in [-Inf, Inf]
p2(6) -53.5594 1.25436 (estimated) in [-Inf, Inf]
p2(7) 34.6095 1.37299 (estimated) in [-Inf, Inf]
p2(8) -210.237 7.95211 (estimated) in [-Inf, Inf]
p2(9) -2641.55 273.034 (estimated) in [-Inf, Inf]
p2(10) -33.6327 3.05742 (estimated) in [-Inf, Inf]
p2(11) -50.9269 1.64086 (estimated) in [-Inf, Inf]
p3 Aerodynamic compensation factor [1/(s*rad)] -0.640669 0.706338 (estimated) in [-Inf, Inf]
p4 Body diameter [m] 0.17 0 (fixed) in [-Inf, Inf]
p5 Body reference area [m^2] 0.0227 0 (fixed) in [-Inf, Inf]
p6(1) Moment of inertia, x-y-z [kg*m^2, kg..] 0.5 0 (fixed) in [-Inf, Inf]
p6(2) 110 0 (fixed) in [-Inf, Inf]
p6(3) 110 0 (fixed) in [-Inf, Inf]
p7 Mass [kg] 107 0 (fixed) in [-Inf, Inf]
p8 Feedback gain [-] 6 0 (fixed) in [-Inf, Inf]
Name: Model
Status:
Termination condition: Maximum number of iterations or number of function evaluations reached..
Number of iterations: 21, Number of function evaluations: 22
Estimated using Solver: ode45; Search: lsqnonlin on time domain data "Data".
Fit to estimation data: [52.93;94.91;91.4;96.07;98.84]%
FPE: 4.627e-10, MSE: 1.672
More information in model's "Report" property.
Model Properties
結果のまとめ
推定されたモデルは、異なる制御戦略の基本性能を調査する際の開始点として良好です。物理的な解釈を望ましくもつ高忠実度モデルには、たとえば、いわゆる「モデル予測制御システム」の重要なコンポーネントがあります。
