このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
同定による複雑なシステムの線形近似
この例では、線形モデルの同定により、複雑な非線形システムの線形近似を取得する方法を説明します。この方法は、システムを励起する入力信号の選択に基づいています。線形近似は、選択した入力信号の非線形モデルをシミュレーションした応答に線形モデルを適合することで得られます。
この例では Simulink®、Control System Toolbox™ および Simulink Control Design™ を使用します。
はじめに
多くの場合、線形モデルは、複数の局所的条件により複雑になっている非線形システムを単純化することにより得ます。たとえば、航空機のダイナミクスの忠実度の高いモデルは詳細な Simulink モデルで表すことができます。このようなシステムのシミュレーションの高速化、操作点での局所的動作の調査、補償器の設計を行うための一般的な方法として、システムの線形化が用いられます。操作点に関して元のモデルを解析的に線形化すると、通常は元のモデルの状態と同じ数または近い数の次数のモデルが得られます。解析または制御システム設計で使用すると、この次数は入力のクラスに対して必要以上に高くなる場合があります。そのため、システムのシミュレーションから入出力データを収集し、そのデータを使用して目的の次数の線形モデルを生成するための代替方式を検討することが必要になる場合もあります。
F14 モデルの解析的な線形化
F14 モデルを考えます。このモデルは既に線形モデルですが、Derivative ブロックと外乱の原因が含まれているため、出力の特性に影響が生じる場合があります。次のように、1 つの入力端子と 2 つの出力端子の間でこのモデルを "線形化" することができます。
open_system('idF14Model') IO = getlinio('idF14Model') syslin = linearize('idF14Model',IO)
3x1 vector of Linearization IOs:
--------------------------
1. Linearization input perturbation located at the following signal:
- Block: idF14Model/Pilot
- Port: 1
- Signal Name: Stick Input
2. Linearization output measurement located at the following signal:
- Block: idF14Model/Gain5
- Port: 1
- Signal Name: Angle of Attack
3. Linearization output measurement located at the following signal:
- Block: idF14Model/Pilot G force
- Port: 1
- Signal Name: Pilot G force
syslin =
A =
Transfer Fcn Derivative Transfer Fcn Derivative1
Transfer Fcn -0.6385 0 689.4 0
Derivative 1 -1e+05 0 0
Transfer Fcn -0.00592 0 -0.6571 0
Derivative1 0 0 1 -1e+05
Actuator Mod 0 0 1.424 0
Alpha-sensor 0.001451 0 0 0
Stick Prefil 0 0 0 0
Pitch Rate L 0 0 1 0
Proportional 0 0 -0.8156 0
Actuator Mod Alpha-sensor Stick Prefil Pitch Rate L
Transfer Fcn -1280 0 0 0
Derivative 0 0 0 0
Transfer Fcn -137.7 0 0 0
Derivative1 0 0 0 0
Actuator Mod -20 2.986 -39.32 -1.67
Alpha-sensor 0 -2.526 0 0
Stick Prefil 0 0 -22.52 0
Pitch Rate L 0 0 0 -4.144
Proportional 0 -1.71 22.52 0.9567
Proportional
Transfer Fcn 0
Derivative 0
Transfer Fcn 0
Derivative1 0
Actuator Mod -3.864
Alpha-sensor 0
Stick Prefil 0
Pitch Rate L 0
Proportional 0
B =
Stick Input
Transfer Fcn 0
Derivative 0
Transfer Fcn 0
Derivative1 0
Actuator Mod 0
Alpha-sensor 0
Stick Prefil 1
Pitch Rate L 0
Proportional 0
C =
Transfer Fcn Derivative Transfer Fcn Derivative1
Angle of Att 0.001451 0 0 0
Pilot G forc -3106 3.106e+08 7.083e+04 -7.081e+09
Actuator Mod Alpha-sensor Stick Prefil Pitch Rate L
Angle of Att 0 0 0 0
Pilot G forc 0 0 0 0
Proportional
Angle of Att 0
Pilot G forc 0
D =
Stick Input
Angle of Att 0
Pilot G forc 0
Continuous-time state-space model.

syslin は 2 つの出力、1 つの入力、9 つの状態があるモデルです。これは、"Stick Input" 入力から 2 つの出力への線形化パスに元のシステムの 9 つの状態が含まれているためです。これは operpoint を使用して検証できます。
operpoint('idF14Model')
ans = Operating point for the Model idF14Model. (Time-Varying Components Evaluated at time t=0) States: ---------- x _ (1.) idF14Model/Actuator Model 0 (2.) idF14Model/Aircraft Dynamics Model/Transfer Fcn.1 0 (3.) idF14Model/Aircraft Dynamics Model/Transfer Fcn.2 0 (4.) idF14Model/Controller/Alpha-sensor Low-pass Filter 0 (5.) idF14Model/Controller/Pitch Rate Lead Filter 0 (6.) idF14Model/Controller/Proportional plus integral compensator 0 (7.) idF14Model/Controller/Stick Prefilter 0 (8.) idF14Model/Dryden Wind Gust Models/Q-gust model 0 (9.) idF14Model/Dryden Wind Gust Models/W-gust model 0 0 Inputs: None ----------
この次数を低くし、一方で選択した矩形波 ("Stick input") 入力に対する応答の忠実度を維持することは可能でしょうか。
同定データの準備
モデルをシミュレーションし、0:30 秒間の入力矩形波 (u) と出力 "Angle of attack" (y1) および "Pilot G force" (y2) のログを生成します。このデータは、等間隔の時間ベクトル (サンプル時間 0.0444 秒) への内挿の後に、"idF14SimData.mat" ファイルに保存されます。
load idF14SimData Z = iddata([y1, y2],u,Ts,'Tstart',0); Z.InputName = 'Stick input'; Z.InputUnit = 'rad/s'; Z.OutputName = {'Angle of attack', 'Pilot G force'}; Z.OutputUnit = {'rad', 'g'}; t = Z.SamplingInstants; subplot(311) plot(t,Z.y(:,1)), ylabel('Angle of attack (rad)') title('Logged Input-Output Data') subplot(312) plot(t,Z.y(:,2)), ylabel('Pilot G force (g)') subplot(313) plot(t,Z.u), ylabel('Stick input (rad/s)') axis([0 30 -1.2 1.2]) xlabel('Time (seconds)')

状態空間モデルの推定
ssest コマンドを使用して、次数 2 ~ 4 の状態空間モデルを推定します。ここでは、推定で "シミュレーション" フォーカスを使用するよう設定し、モデルの外乱コンポーネントを推定しないよう選択します。
opt = ssestOptions('Focus','simulation'); syslin2 = ssest(Z, 2, 'DisturbanceModel', 'none', opt); syslin3 = ssest(Z, 3, 'DisturbanceModel', 'none', opt); syslin4 = ssest(Z, 4, 'DisturbanceModel', 'none', opt);
線形化されたモデル syslin と 3 つの同定されたモデルのパフォーマンスをデータと比較します。syslin は SS モデルで、syslin2、syslin3、syslin4 は IDSS モデルです。
syslin.InputName = Z.InputName;
syslin.OutputName = Z.OutputName; % reconcile names to facilitate comparison
clf
compare(Z, syslin, syslin2, syslin3, syslin4)

プロットからは、3 次モデル (syslin3) が既定 (t=0) の操作条件に関する航空機のダイナミクスの線形近似として十分に機能していることがわかります。解析的な線形化により得られたもの (syslin) と比べて、データの適合はやや優れたものとなっています。元の idF14Model が線形の場合、線形化の結果 (syslin) がデータと 100% 適合しないのはなぜでしょうか。これには 2 つの理由があります。
測定された出力は突風の影響を受けています。そのため、ログに記録された出力は Stick input の単なる関数ではありません。外乱が影響を及ぼしています。
"Pilot G force" ブロックでは Derivative ブロックが使用されていて、線形化は時定数 "c" の値に依存しています。"c" の値は小さくしなければなりませんが (ここでは 1e-5 を使用します)、0 にはならないようにします。c の値が 0 以外の場合、線形化で近似誤差が発生します。
モデル syslin3 のパラメーターを見てみましょう。応答は十分に再現されているようです。
syslin3
syslin3 =
Continuous-time identified state-space model:
dx/dt = A x(t) + B u(t) + K e(t)
y(t) = C x(t) + D u(t) + e(t)
A =
x1 x2 x3
x1 -1.006 2.029 0.5842
x2 -8.284 -19.39 5.611
x3 2.784 12.63 -6.956
B =
Stick input
x1 0.2614
x2 -5.512
x3 3.606
C =
x1 x2 x3
Angle of att -8.841 0.5347 1.402
Pilot G forc -86.42 15.85 66.12
D =
Stick input
Angle of att 0
Pilot G forc 0
K =
Angle of att Pilot G forc
x1 0 0
x2 0 0
x3 0 0
Parameterization:
FREE form (all coefficients in A, B, C free).
Feedthrough: none
Disturbance component: none
Number of free coefficients: 18
Use "idssdata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using SSEST on time domain data "Z".
Fit to estimation data: [98.4;97.02]%
FPE: 2.367e-05, MSE: 0.1103
低次元化と推定によるモデルの単純化
また、線形化されたモデル syslin を低次元化し、この低次元化されたモデルのパラメーターがデータ Z に最もよく適合するように調整するという方法もあります。低次元化のための適切な値を求めるには、hsvd を使用します。
[S, BalData] = hsvd(syslin); clf; bar(S)

棒グラフからは、状態 4 以降では特異値が非常に小さいことがわかります。そのため、低次元化して 3 次にするのが最適と考えられます。
sysr = balred(syslin,3,BalData)
opt2 = bodeoptions; opt2.PhaseMatching = 'on';
clf; bodeplot(sysr,syslin,opt2)
sysr =
A =
x1 x2 x3
x1 -2.854 -7.61 -54.04
x2 -0.9714 2.341 9.123
x3 0.6979 -7.203 -24.08
B =
Stick input
x1 -137.7
x2 -869
x3 -506.7
C =
x1 x2 x3
Angle of att -0.0005063 -0.0008826 -0.001016
Pilot G forc -0.005926 -0.04692 -0.1646
D =
Stick input
Angle of att -0.03784
Pilot G forc -1.617
Continuous-time state-space model.
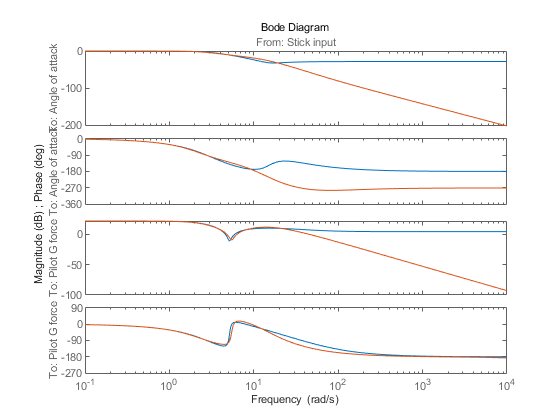
ボード線図は 10 rad/s の高い忠実度を示しています。sysr は compare プロットが示すように、状態が 9 つある元のモデルと同じ程度に応答をエミュレートできます。
compare(Z, sysr, syslin)

sysr のパラメーターを調整して、データとの適合を改善します。この推定では、"Levenberg-Marquardt" 検索方式を選択し、許容できる反復の最大数を 10 に変更します。これらの選択は試行錯誤で行われます。また、推定の進捗状況の表示もオンにします。
opt.Display = 'on'; opt.SearchMethod = 'lm'; opt.SearchOptions.MaxIterations = 10; sysr2 = ssest(Z, sysr, opt) compare(Z, sysr2)
sysr2 =
Continuous-time identified state-space model:
dx/dt = A x(t) + B u(t) + K e(t)
y(t) = C x(t) + D u(t) + e(t)
A =
x1 x2 x3
x1 -4.048 -7.681 -54.01
x2 -0.4844 1.549 8.895
x3 -0.2398 -6.777 -25.78
B =
Stick input
x1 -137.7
x2 -869
x3 -506.7
C =
x1 x2 x3
Angle of att -0.0003361 -0.0004964 0.00215
Pilot G forc -0.01191 -0.03599 -0.1434
D =
Stick input
Angle of att 0.003022
Pilot G forc 0.6438
K =
Angle of att Pilot G forc
x1 0 0
x2 0 0
x3 0 0
Parameterization:
FREE form (all coefficients in A, B, C free).
Feedthrough: yes
Disturbance component: none
Number of free coefficients: 20
Use "idssdata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using SSEST on time domain data "Z".
Fit to estimation data: [98.78;97.03]%
FPE: 1.434e-05, MSE: 0.1097


改善されたモデル sysr2 は F14 モデルの応答と非常によく一致しています (最初の出力では約 99%、次の出力では 97%)。
まとめ
ここでは、複雑なシステムの線形近似を取得するための、解析的な線形化にかわる代替方法について説明しました。結果は特定の入力信号から生成され、厳密に言えばその入力に対してしか適用できません。結果をさまざまな入力プロファイルに適用できるようにするには、各種の入力を使用して複数のシミュレーションを実行します。その後、生成されたデータセットを 1 つの複数実験データセットに結合し (iddata/merge を参照)、これを使用して推定を実行します。この例では、わかりやすいように、複雑ではありますが線形のシステムを使用しました。この方式の実際の利点は、非線形システムで見られます。
また、線形システムを低次元化し、その一方で低次元化されたモデルが元の Simulink モデルのシミュレーションされた応答に忠実になるようにする方法についても説明しました。低次元化されたモデル sysr の役割は、推定されたモデル sysr2 の初期推定を生成することです。この手法では、線形システムであれば、クラスが異なっていても、推定の初期モデルとして使用できます。
bdclose('idF14Model')
