4-Way 3-Position Directional Valve (G)
Controlled valve with four ports in a gas network
Libraries:
Simscape /
Fluids /
Gas /
Valves & Orifices /
Directional Control Valves
Description
The 4-Way 3-Position Directional Valve (G) block represents a valve with four gas ports (P, A, B, and T) and flow paths between P–A and A–T and between P–B and B–T. The paths each run through an orifice of variable width. The input signal specified at port S controls the position of the spool. The valve closes when the spool covers the orifice opening.
In a representative system, the P port connects to the pump, the T port connects to the tank, and the A and B ports connect to a double-sided actuator. Opening the P–A and B–T flow paths allows the pump to pressurize one side of the actuator and the tank to relieve the other. The actuator shaft translates to extend in some systems and retract in others. Opening the P–B and A–T flow paths flips the pressurized and relieved sides of the actuator so that the shaft can translate in reverse.
This image shows a common use for a four-way, three-position directional valve in a physical system:

The flow can be laminar or turbulent, and it can reach up to sonic speeds. The maximum velocity happens at the throat of the valve where the flow is narrowest and fastest. The flow chokes and the velocity saturates when a drop in downstream pressure can no longer increase the velocity. Choking occurs when the back-pressure ratio reaches the critical value characteristic of the valve. The block does not capture supersonic flow.
Valve Positions
The valve is continuously variable and it shifts smoothly between one normal and two working positions.
When the instantaneous displacement of the spool at port S is zero, the valve reverts to the normal position where it is no longer operating. Unless the lands of the spool are at an offset to their orifices, the valve is fully closed. The working positions are the positions the valve moves to when the spool is maximally displaced from its normal position. That displacement is positive in one case and negative in the other.
Image I shows a valve where the displacement is positive, the P–A and B–T orifices are fully open, and the P–B and A–T orifices are fully closed. Image II shows a valve where the displacement is negative, the P–A and B–T orifices are fully closed, and the P–B and A–T orifices are fully open. Image III shows a valve where the spool is in the neutral position and all the orifices are closed.
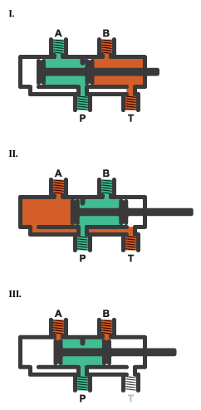
The spool displacement that puts the valve in its working position depends on the offsets of the lands on the spool. The parameters in the Valve Opening Fraction Offsets section specify the block constants for the spool displacements of the ports.
Between valve positions, the opening of an orifice depends on where the land of the spool is, relative to the rim. This distance is the orifice opening, and the block normalizes this distance so that its value is a fraction of the maximum distance at which the orifice is fully open. The normalized variable is the orifice opening fraction.
The orifice opening fractions range from -1 when the valve is in the
position shown in image I to
+1 when the valve is in the position shown in image
II.
The block calculates the opening fractions from the spool displacement and opening fraction offset. The displacement and offset are unitless fractions of the maximum land-orifice distance.
The opening fraction of the P–A orifice is:
The opening fraction of the B–T orifice is:
The opening fraction of the A–T orifice is:
The opening fraction of the P–B orifice is:
In the equations:
h is the opening fraction for the orifice. If the calculation returns a value outside of the range
0 - 1, the block uses the nearest limit.H is the opening fraction offset for the orifice. The parameters in the Valve Opening Fraction Offsets section specify the opening fraction offsets. To allow for unusual valve configurations, the block imposes no limit on their values, although they are typically between
-1and+1.x is the normalized instantaneous displacement of the spool, specified by a physical signal at port S. To compensate for extreme opening fraction offsets, there is no limit on the signal value. The value is typically between
-1and+1.
By default, the valve is fully closed when its control displacement is zero. In this state, the valve is zero-lapped.
You can offset the lands of the spool to model an underlapped or overlapped valve. Underlapped valves are partially open in the normal position. Overlapped valves are fully closed slightly beyond the normal position. The figure shows how the orifice opening fractions vary with the instantaneous spool displacement:
Image I: A zero-lapped valve. The opening fraction offsets are all zero. When the valve is in the normal position, the lands of the spool completely cover all four orifices.
Image II: An underlapped valve. The P–A and B–T opening fraction offsets are positive and the P–B and the A–T opening fraction offsets are negative. When the valve is in the normal position, the lands of the spool partially cover the four orifices.
Image III: An overlapped valve. The P–A and B–T opening fraction offsets are negative and the P–B and the A–T opening fraction offsets are positive. The control member completely covers all orifices not only in the normal position but over a small region of spool displacements around it.

Valve Parameterizations
The block behavior depends on the Valve parametrization parameter:
Cv flow coefficient— The flow coefficient Cv determines the block parameterization. The flow coefficient measures the ease with which a gas can flow when driven by a certain pressure differential. [2][3]Kv flow coefficient— The flow coefficient Kv, where , determines the block parameterization. The flow coefficient measures the ease with which a gas can flow when driven by a certain pressure differential. [2][3]Sonic conductance— The sonic conductance of the resistive element at steady state determines the block parameterization. The sonic conductance measures the ease with which a gas can flow when choked, which is a condition in which the flow velocity is at the local speed of sound. Choking occurs when the ratio between downstream and upstream pressures reaches a critical value known as the critical pressure ratio. [1]Orifice area— The size of the flow restriction determines the block parametrization. [4]
Opening Characteristics
The flow characteristic relates the opening of the valve to the input that produces it, which is often the spool travel. The block expresses the opening as a sonic conductance, flow coefficient, or restriction area, depending on the setting of the Valve parameterization parameter. The control input is the orifice opening fraction, a function of the spool displacement specified at port S.
The flow characteristic is normally given at steady state, with the inlet at a constant, carefully controlled pressure. The flow characteristic depends only on the valve and can be linear or nonlinear. To capture the flow characteristics, use the Opening characteristic parameter:
Linear— The measure of flow capacity is a linear function of the orifice opening fraction. As the opening fraction rises from0to1, the measure of flow capacity scales from the specified minimum to the specified maximum.
Tabulated— The measure of flow capacity is a general function, which can be linear or nonlinear, of the orifice opening fraction. The function is specified in tabulated form, with the independent variable specified by the Opening fraction vector.
Numerical Smoothing
When the Opening characteristic parameter is
Linear, and the Smoothing factor
parameter is nonzero, the block applies numerical smoothing to the orifice opening
fraction. Enabling smoothing helps maintain numerical robustness in your
simulation.
For more information, see Numerical Smoothing.
Leakage Flow
The leakage flow ensures that no section of a fluid network becomes isolated. Isolated fluid sections can reduce the numerical robustness of the model, slow the rate of simulation and, in some cases, cause the simulation to fail. The Leakage flow fraction parameter represents the leakage flow area in the block as a small number greater than zero.
Composite Structure
This block is a composite component comprising four instances of the Orifice (G) block connected to ports P, A, B, T, and S. Refer to the Orifice (G) block for more detail on the valve parameterizations and block calculations.
Assumptions and Limitations
The
Sonic conductancesetting of the Valve parameterization parameter is for pneumatic applications. If you use this setting for gases other than air, you may need to scale the sonic conductance by the square root of the specific gravity.The equation for the
Orifice area based on geometryparameterization is less accurate for gases that are far from ideal.This block does not model supersonic flow.
Examples
Ports
Input
Conserving
Parameters
References
[1] ISO 6358-3. "Pneumatic fluid power – Determination of flow-rate characteristics of components using compressible fluids – Part 3: Method for calculating steady-state flow rate characteristics of systems". 2014.
[2] IEC 60534-2-3. "Industrial-process control valves – Part 2-3: Flow capacity – Test procedures". 2015.
[3] ANSI/ISA-75.01.01. "Industrial-Process Control Valves – Part 2-1: Flow capacity – Sizing equations for fluid flow underinstalled conditions". 2012.
[4] P. Beater. Pneumatic Drives. Springer-Verlag Berlin Heidelberg. 2007.

