Optimize Function Using simulannealbnd, Problem-Based

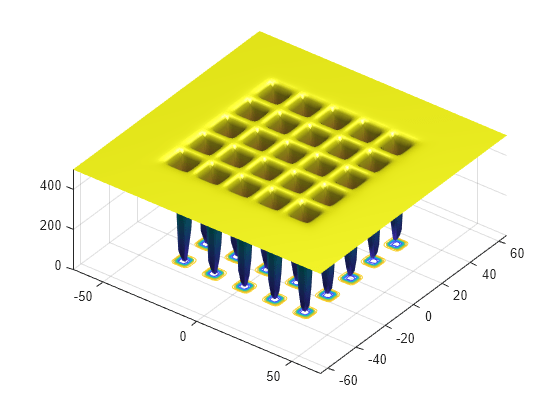
This example shows how to minimize a function using simulated annealing in the problem-based approach when the objective is a function file, possibly of unknown content (a "black box" function). The function to minimize, dejong5fcn(x), is available when you run this example. Plot the function.

dejong5fcn

Create a 2-D optimization variable x. The dejong5fcn function expects the variable to be a row vector, so specify x as a 2-element row vector.

x = optimvar("x",1,2);

To use dejong5fcn as the objective function, convert the function to an optimization expression using fcn2optimexpr.

fun = fcn2optimexpr(@dejong5fcn,x);

Create an optimization problem with the objective function fun.

prob = optimproblem("Objective",fun);

Set variable bounds from –50 to 50 in all components. When you specify scalar bounds, the software expands the bounds to all variables.

x.LowerBound = -50;
x.UpperBound = 50;

Set a pseudorandom initial point within the bounds. The initial point is a structure with field x.

rng default % For reproducibility
x0.x = x.LowerBound + rand(size(x.LowerBound)).*x.UpperBound;

Solve the problem, specifying the simulannealbnd solver.

[sol,fval] = solve(prob,x0,"Solver","simulannealbnd")

Solving problem using simulannealbnd.
simulannealbnd stopped because the change in best function value is less than options.FunctionTolerance.

sol = struct with fields:
    x: [-32.0371 -31.8792]

fval = 
0.9980