このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

paretosearch と gamultiobj の比較

ライブ スクリプトを開く

この例では、paretosearch と gamultiobj の両方を使用して、パレート フロント上にポイントのセットを作成する方法を示します。目的関数には 2 つの目的と 2 次元の制御変数 x があります。ボタンをクリックしてこの例を編集または試すと、目的関数 mymulti3 が MATLAB ® セッションで使用できるようになります。あるいは、mymulti3 コードをセッションにコピーします。計算速度を上げるため、関数はベクトル化されます。

type mymulti3
function f = mymulti3(x)
%
f(:,1) = x(:,1).^4 + x(:,2).^4 + x(:,1).*x(:,2) - (x(:,1).^2).*(x(:,2).^2) - 9*x(:,1).^2;
f(:,2) = x(:,2).^4 + x(:,1).^4 + x(:,1).*x(:,2) - (x(:,1).^2).*(x(:,2).^2) + 3*x(:,2).^3;

基本的な例とプロット

paretosearch と gamultiobj を使用して、目的関数のパレート集合を見つけます。速度を上げるには、UseVectorized オプションを true に設定します。パレート集合を視覚化するためのプロット関数を含めます。

rng default
nvars = 2;
opts = optimoptions(@gamultiobj,'UseVectorized',true,'PlotFcn','gaplotpareto');
[xga,fvalga,~,gaoutput] = gamultiobj(@(x)mymulti3(x),nvars,[],[],[],[],[],[],[],opts);
gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.

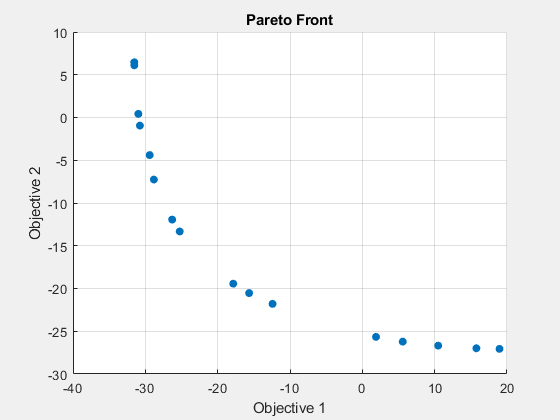
Figure Genetic Algorithm contains an axes object. The axes object with title Pareto Front, xlabel Objective 1, ylabel Objective 2 contains an object of type scatter.

optsp = optimoptions('paretosearch','UseVectorized',true,'PlotFcn',{'psplotparetof' 'psplotparetox'});
[xp,fvalp,~,psoutput] = paretosearch(@(x)mymulti3(x),nvars,[],[],[],[],[],[],[],optsp);
Pareto set found that satisfies the constraints. 

Optimization completed because the relative change in the volume of the Pareto set 
is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 
'options.ConstraintTolerance'.

Figure paretosearch contains 2 axes objects. Axes object 1 with title Pareto Front, xlabel Objective 1, ylabel Objective 2 contains an object of type scatter. Axes object 2 with title Parameter Space, xlabel Parameter 1, ylabel Parameter 2 contains an object of type scatter.

mymulti4 を使用して、パレート フロント上の理論的に正確な点を計算します。この例を編集または試すためにボタンをクリックすると、mymulti4 関数が MATLAB セッションで使用できるようになります。

type mymulti4
function mout = mymulti4(x)
%
gg = [4*x(1)^3+x(2)-2*x(1)*(x(2)^2) - 18*x(1);
    x(1)+4*x(2)^3-2*(x(1)^2)*x(2)];
gf = gg + [18*x(1);9*x(2)^2];

mout = gf(1)*gg(2) - gf(2)*gg(1);

mymulti4 関数は 2 つの目的関数の勾配を評価します。次に、x(2) の値の範囲について、fzero を使用して勾配が完全に平行になる点、つまり出力 mout = 0 となる点を見つけます。

a = [fzero(@(t)mymulti4([t,-3.15]),[2,3]),-3.15];
for jj = linspace(-3.125,-1.89,50)
    a = [a;[fzero(@(t)mymulti4([t,jj]),[2,3]),jj]];
end
figure
plot(fvalp(:,1),fvalp(:,2),'bo');
hold on
fs = mymulti3(a);
plot(fvalga(:,1),fvalga(:,2),'r*');
plot(fs(:,1),fs(:,2),'k.')
legend('Paretosearch','Gamultiobj','True')
xlabel('Objective 1')
ylabel('Objective 2')
hold off

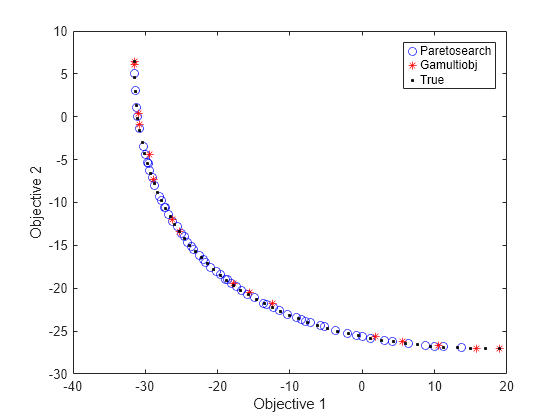
Figure contains an axes object. The axes object with xlabel Objective 1, ylabel Objective 2 contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent Paretosearch, Gamultiobj, True.

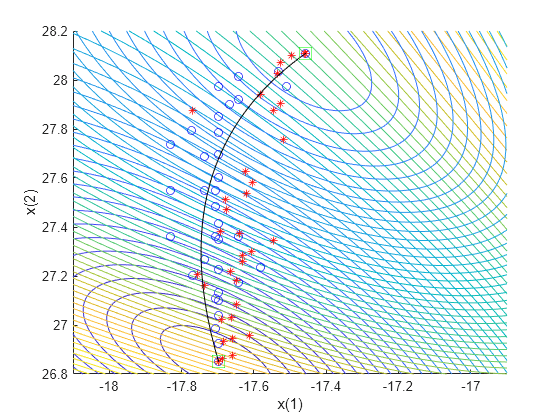
gamultiobj は、目的関数空間内でわずかに広い範囲に渡るポイントを見つけます。理論上の最適なパレート曲線と 2 つの目的関数の等高線図とともに、決定変数空間にソリューションをプロットします。

[x,y] = meshgrid(1.9:.01:3.1,-3.2:.01:-1.8);
mydata = mymulti3([x(:),y(:)]);
myff = sqrt(mydata(:,1) + 39);% Spaces the contours better
mygg = sqrt(mydata(:,2) + 28);% Spaces the contours better
myff = reshape(myff,size(x));
mygg = reshape(mygg,size(x));

figure;
hold on
contour(x,y,mygg,50)
contour(x,y,myff,50)
plot(xp(:,1),xp(:,2),'bo')
plot(xga(:,1),xga(:,2),'r*')
plot(a(:,1),a(:,2),'-k')
xlabel('x(1)')
ylabel('x(2)')
hold off

Figure contains an axes object. The axes object with xlabel x(1), ylabel x(2) contains 5 objects of type contour, line. One or more of the lines displays its values using only markers

paretosearch ソリューションとは異なり、gamultiobj ソリューションでは、目的関数空間の範囲の両端に点が存在します。ただし、paretosearch ソリューションには、目的関数空間と決定変数空間の両方で真のソリューションに近いポイントが多くあります。デフォルト オプションを使用する場合、パレート フロント上のポイントの数はソルバーごとに異なります。

シフトした問題

問題の解決策に大きな制御変数がある場合はどうなるでしょうか?問題の変数をシフトしてこのケースを調べます。制約のない問題の場合、gamultiobj は失敗する可能性がありますが、paretosearch はそのようなシフトに対してより堅牢です。

比較を容易にするために、各ソルバーのパレート フロントに 35 個のポイントを指定します。

shift = [20,-30];
fun = @(x)mymulti3(x+shift);
opts.PopulationSize = 100; % opts.ParetoFraction = 35
[xgash,fvalgash,~,gashoutput] = gamultiobj(fun,nvars,[],[],[],[],[],[],opts);
gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.

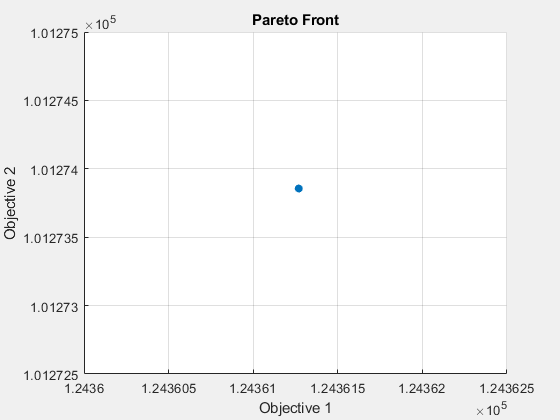
Figure Genetic Algorithm contains an axes object. The axes object with title Pareto Front, xlabel Objective 1, ylabel Objective 2 contains an object of type scatter.

gamultiobj は有用なパレート集合を見つけることができません。

optsp.PlotFcn = [];
optsp.ParetoSetSize = 35;
[xpsh,fvalpsh,~,pshoutput] = paretosearch(fun,nvars,[],[],[],[],[],[],[],optsp);
Pareto set found that satisfies the constraints. 

Optimization completed because the relative change in the volume of the Pareto set 
is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 
'options.ConstraintTolerance'.

figure
plot(fvalpsh(:,1),fvalpsh(:,2),'bo');
hold on
plot(fs(:,1),fs(:,2),'k.')
legend('Paretosearch','True')
xlabel('Objective 1')
ylabel('Objective 2')
hold off

Figure contains an axes object. The axes object with xlabel Objective 1, ylabel Objective 2 contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Paretosearch, True.

paretosearch は、ほぼ全範囲にわたって均等に広がる解のポイントを見つけます。

たとえかなり緩いものであっても、境界を追加すると、gamultiobj と paretosearch の両方が適切な解決策を見つけるのに役立ちます。各コンポーネントの -50 の下限と 50 の上限を設定します。

opts.PlotFcn = [];
optsp.PlotFcn = [];
lb = [-50,-50];
ub = -lb;
[xgash,fvalgash,~,gashoutput] = gamultiobj(fun,nvars,[],[],[],[],lb,ub,opts);
gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.

[xpsh2,fvalpsh2,~,pshoutput2] = paretosearch(fun,nvars,[],[],[],[],lb,ub,[],optsp);
Pareto set found that satisfies the constraints. 

Optimization completed because the relative change in the volume of the Pareto set 
is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 
'options.ConstraintTolerance'.

figure
plot(fvalpsh2(:,1),fvalpsh2(:,2),'bo');
hold on
plot(fvalgash(:,1),fvalgash(:,2),'r*');
plot(fs(:,1),fs(:,2),'k.')
legend('Paretosearch','Gamultiobj','True')
xlabel('Objective 1')
ylabel('Objective 2')
hold off

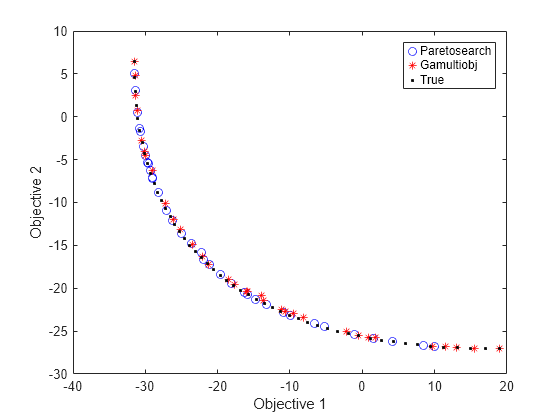
Figure contains an axes object. The axes object with xlabel Objective 1, ylabel Objective 2 contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent Paretosearch, Gamultiobj, True.

この場合、両方のソルバーが適切な解決策を見つけます。

gamultiobj から paretosearch を開始する

gamultiobj ソリューションから paretosearch を開始して、ソルバーから同様の範囲のソリューションを取得します。

optsp.InitialPoints = xgash;
[xpsh3,fvalpsh3,~,pshoutput3] = paretosearch(fun,nvars,[],[],[],[],lb,ub,[],optsp);
Pareto set found that satisfies the constraints. 

Optimization completed because the relative change in the volume of the Pareto set 
is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 
'options.ConstraintTolerance'.

figure
plot(fvalpsh3(:,1),fvalpsh3(:,2),'bo');
hold on
plot(fvalgash(:,1),fvalgash(:,2),'r*');
plot(fs(:,1),fs(:,2),'k.')
legend('Paretosearch','Gamultiobj','True')
xlabel('Objective 1')
ylabel('Objective 2')
hold off

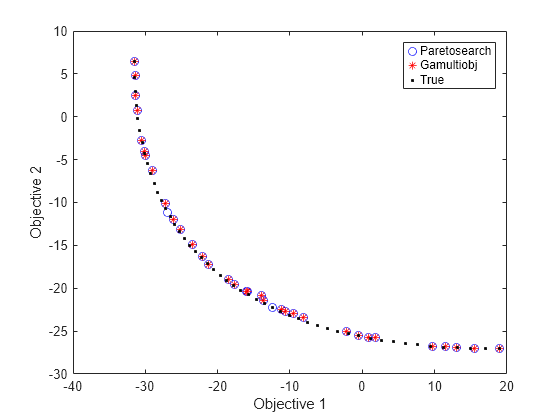
Figure contains an axes object. The axes object with xlabel Objective 1, ylabel Objective 2 contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent Paretosearch, Gamultiobj, True.

現在、paretosearch ソリューションは gamultiobj ソリューションに似ていますが、いくつかのソリューション ポイントは異なります。

単一目的のソリューションから始める

適切なソリューションを得るためのもう 1 つの方法は、各目的関数を個別に最小化するポイントから開始することです。

多目的関数から、各目的を順番に選択する単一目的関数を作成します。前のセクションのシフト関数を使用します。ソルバーに適切な開始点を与えているので、境界を指定する必要はありません。

nobj = 2; % Number of objectives

x0 = -shift; % Initial point for single-objective minimization
uncmin = cell(nobj,1); % Cell array to hold the single-objective minima
allfuns = zeros(nobj,2); % Hold the objective function values
eflag = zeros(nobj,1);
fopts = optimoptions('patternsearch','Display','off'); % Use an appropriate solver here
for i = 1:nobj
    indi = zeros(nobj,1); % Choose the objective to minimize
    indi(i) = 1;
    funi = @(x)dot(fun(x),indi);
    [uncmin{i},~,eflag(i)] = patternsearch(funi,x0,[],[],[],[],[],[],[],fopts); % Minimize objective i
    allfuns(i,:) = fun(uncmin{i});
end
uncmin = cell2mat(uncmin); % Matrix of start points

paretosearch を単一目的の最小点から開始し、その解の範囲が完全であることに注意してください。paretosearch は、少なくとも options.ParetoSetSize 個の個体の母集団を持つように、指定された初期点にランダムな初期点を追加します。同様に、gamultiobj は、提供されたポイントにランダムなポイントを追加して、少なくとも (options.PopulationSize)*(options.ParetoFraction) 個の個体の母集団を取得します。

optsp = optimoptions(optsp,'InitialPoints',uncmin);
[xpinit,fvalpinit,~,outputpinit] = paretosearch(fun,nvars,[],[],[],[],[],[],[],optsp);
Pareto set found that satisfies the constraints. 

Optimization completed because the relative change in the volume of the Pareto set 
is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 
'options.ConstraintTolerance'.

ここで、初期点から始めて gamultiobj を使用して問題を解きます。

opts = optimoptions(opts,'InitialPopulationMatrix',uncmin);
[xgash2,fvalgash2,~,gashoutput2] = gamultiobj(fun,nvars,[],[],[],[],[],[],opts);
gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.

figure
plot(fvalpinit(:,1),fvalpinit(:,2),'bo');
hold on
plot(fvalgash2(:,1),fvalgash2(:,2),'r*');
plot(fs(:,1),fs(:,2),'k.')
plot(allfuns(:,1),allfuns(:,2),'gs','MarkerSize',12)
legend('Paretosearch','Gamultiobj','True','Start Points')
xlabel('Objective 1')
ylabel('Objective 2')
hold off

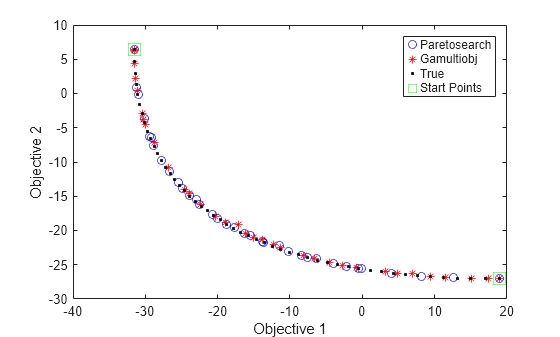
Figure contains an axes object. The axes object with xlabel Objective 1, ylabel Objective 2 contains 4 objects of type line. One or more of the lines displays its values using only markers These objects represent Paretosearch, Gamultiobj, True, Start Points.

どちらのソルバーも、極値間のパレート フロントを、適度に正確で十分な間隔のあるソリューションで埋めます。

決定変数空間の最終ポイントを表示します。

figure;
hold on
xx = x - shift(1);
yy = y - shift(2);
contour(xx,yy,mygg,50)
contour(xx,yy,myff,50)
plot(xpinit(:,1),xpinit(:,2),'bo')
plot(xgash2(:,1),xgash2(:,2),'r*')
ashift = a - shift;
plot(ashift(:,1),ashift(:,2),'-k')
plot(uncmin(:,1),uncmin(:,2),'gs','MarkerSize',12);
xlabel('x(1)')
ylabel('x(2)')
hold off

Figure contains an axes object. The axes object with xlabel x(1), ylabel x(2) contains 6 objects of type contour, line. One or more of the lines displays its values using only markers

参考

|

トピック