Implement HDL-Optimized CORDIC-Based Square Root for Positive Real Numbers
This example shows two implementations of HDL-optimized CORDIC square root in the CORDIC Square Root Resource-Shared block and the CORDIC Square Root Fully-Pipelined block. The first implementation has a resource-shared architecture that is optimized for low hardware utilization. The second implementation has a fully-pipelined architecture that is optimized for high throughput. The core algorithm of both blocks uses CORDIC in hyperbolic vectoring mode to compute the approximation of square root (see Compute Square Root Using CORDIC). This CORDIC-based algorithm is different from the Simulink® Sqrt block, which uses bisection and Newton-Raphson methods. The algorithm in the HDL-optimized CORDIC square root blocks require only iterative shift-add operations.
The input data for this example is a real non-negative scalar. Both blocks use the AMBA AXI handshake protocol at the input and output interfaces.
Generate HDL Code from Resource-Shared Architecture and Fully-Pipelined Architecture
The CORDIC Square Root Resource-Shared block and the CORDIC Square Root Fully-Pipelined block use different architectures for HDL code generation.
Resources-Shared Architecture
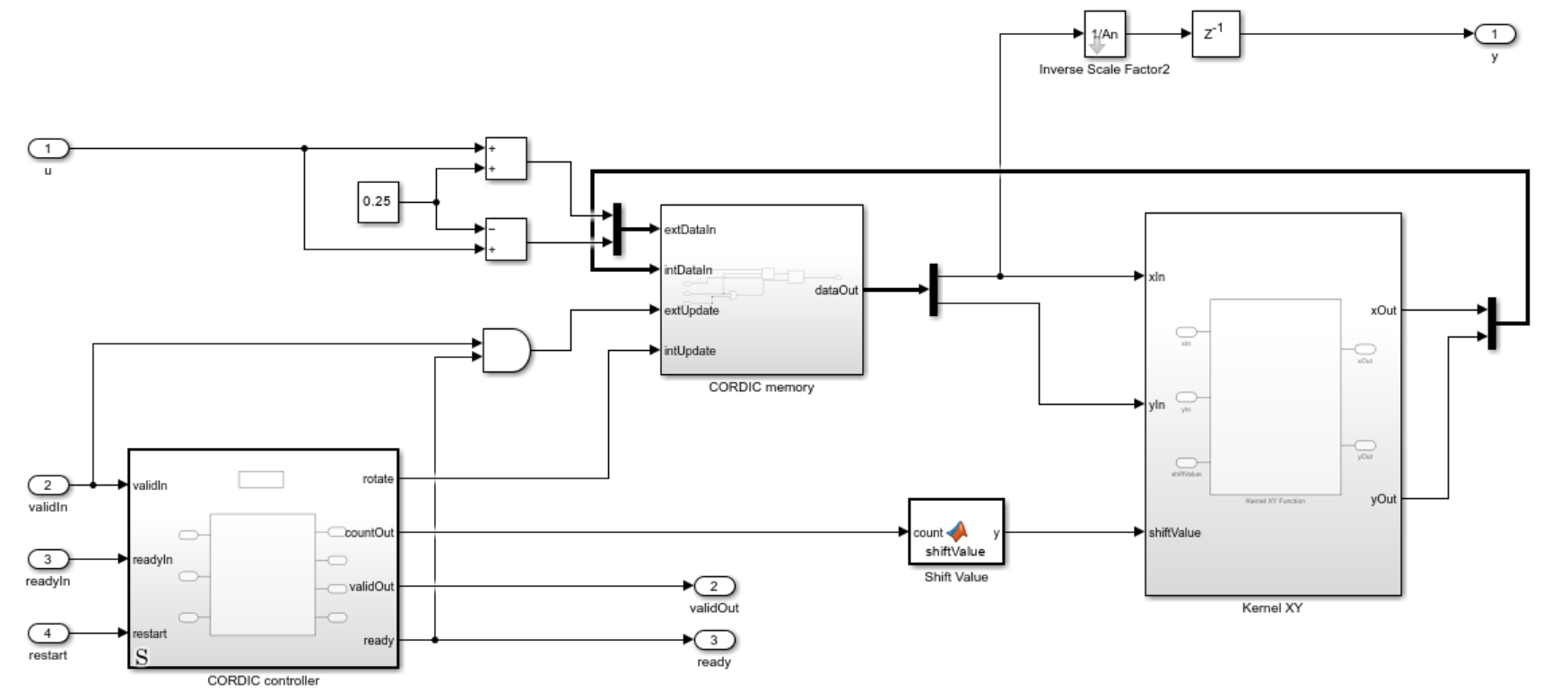
The CORDIC Square Root Resource-Shared block uses a resource-shared architecture. In the generated hardware design, this architecture prioritizes the hardware utilization constraint over throughput. The block has one CORDIC kernel, which is reused for all CORDIC shift-and-add iterations. A controller based on a MATLAB Function block controls the AMBA AXI handshake process and CORDIC workflow. This controller is a Moore machine. The state register and internal counter of the controller are modeled by persistent variables. For guidelines, see Initialize Persistent Variables in MATLAB Functions. The control logic and algorithm data path are intentionally separated for better maintainability and reusability.
Assuming that the upstream block and downstream block are always ready, the block timing diagram is as shown.

The first u input is u1, u2 is the second u input, y1 is the square root of u1, y2 is the square root of u2, and so on.
After a successful input data transaction, this block starts computing the square root approximation. During the computation, the block ignores all other input data. Once the computation is done, the block holds the result at output port and asserts its validOut signal. After a successful output data transaction, the block becomes ready again. The block asserts its ready signal and waits for the input handshake signal.
Fully-Pipelined Architecture
The CORDIC Square Root Fully-Pipelined block uses a fully-pipelined architecture. In the generated hardware design, this architecture prioritizes throughput over hardware utilization constraints. Each CORDIC shift-and-add iteration is performed by a dedicated CORDIC kernel, so the block can accept new data on any clock cycle if its downstream block is available. The cascaded CORDIC structure is implemented by a for-each subsystem with a Unit Delay Enabled Synchronous block, Selector block, and Mux block. The pipeline registers in the data path are modeled by Unit Delay Enabled Synchronous block so the downstream ready signal can control the data flow. A Unit Delay Enabled Resettable Synchronous block models the pipeline registers in the data path. The downstream ready signal controls the valid signal flow, and the restart signal resets the pipeline registers along the valid signal path.

Assuming that the upstream block and downstream block are always ready, the block timing diagram is as shown.

The first u input is u1, u2 is the second u input, y1 is the square root of u1, y2 is the square root of u2, and so on.
After a successful input data transaction, this block computes the square root approximation of the input data. Because of its fully-pipelined nature, the block is able to accept input data on any cycle, including on consecutive cycles. Once the computation is done, the block holds the result at output port, asserts its validOut signal, and waits for the downstream handshake signal. The ready signal is a direct feedthrough of the readyIn signal for back-pressure propagation. If the downstream block is not ready, this block also pauses accordingly.
Define Simulation Parameters
Specify the number of input samples and data type.
numSamples = 3;
Specify the data type as Fixed, Single, or Double.
DT =  'Fixed';
'Fixed';For fixed-point data type, specify the word length and fraction length.
wordLength = 16; FractionLength = 10;
Define the maximum CORDIC shift value. In fixed point, this value cannot exceed wordLength - 1.
switch lower(DT) case 'fixed' maximumShiftValue = wordLength - 1; case 'single' maximumShiftValue = 23; case 'double' maximumShiftValue = 52; otherwise maximumShiftValue = 52; end
Generate Nonnegative Input u
rng('default');
u = abs(randn(1,numSamples));Cast to Selected Data Type
switch lower(DT) case 'fixed' u = cast(u,'like',fi([],1,wordLength,FractionLength)); case 'single' u = single(u); case 'double' u = double(u); otherwise u = double(u); end
Configure Model Workspace and Run Simulation
model = 'CORDICSquareRootHDLOptimizedModel'; open_system(model); fixed.example.setModelWorkspace(model,'u',u,'numSamples',numSamples,'maximumShiftValue',maximumShiftValue); out = sim(model);

Verify Output Solutions
Compare fixed-point results with built-in floating point results.
yBuiltIn = sqrt(double(u))'
yBuiltIn = 3×1
0.7335
1.3542
1.5029
yShared = out.yShared
yShared =
0.7334
1.3535
1.5029
DataTypeMode: Fixed-point: binary point scaling
Signedness: Signed
WordLength: 16
FractionLength: 10
yPipelined = out.yPipelined(1:numSamples)
yPipelined =
0.7334
1.3535
1.5029
DataTypeMode: Fixed-point: binary point scaling
Signedness: Signed
WordLength: 16
FractionLength: 10
Verify that the CORDIC Square Root Resource-Shared block and the CORDIC Square Root Fully-Pipelined block return identical results in fixed point.
if strcmpi(DT,'fixed') yShared == yPipelined %#ok end
ans = 3×1 logical array
1
1
1
Block Latency Equations
The block latency is the number of clock cycles between a successful input and when the corresponding output becomes valid.
The CORDIC-based square root approximation has two main steps: normalization and CORDIC shift-add iterations. Thus, the total latency is normalization latency plus the latency of the CORDIC shift-add iterations.
The latency of normalization is determined by the input word length.
if isfi(u) && isfixed(u) % If input is fi, normalization latency is nextpow2(u.WordLength)+1. normLatency = nextpow2(u.WordLength)+1; else % If input is floating point, normalization latency is 0. normLatency = 0; end
The number of CORDIC iterations is determined by the CORDIC maximum shift value. This example uses wordLength - 1 for best precision.
sequence = fixed.cordic.hyperbolic.shiftSequence(maximumShiftValue); numOfCORDICIterations = length(sequence);
CORDIC Square Root Resource-Shared Block
For the resource-shared architecture, the CORDIC shift-add iterations latency is the number of CORDIC iterations plus two.
blockLatencySharedSim = normLatency + numOfCORDICIterations + 2 %#okblockLatencySharedSim = 24
After a successful output, the resource-shared block becomes ready in the next clock cycle.
CORDIC Square Root Fully-Pipelined Block
For the fully-pipelined architecture, the CORDIC shift-add iterations latency is the number of CORDIC iterations plus one.
blockLatencyPipelined = normLatency + numOfCORDICIterations + 1
blockLatencyPipelined = 23
When the downstream block is available, the CORDIC Square Root Fully-Pipelined block can accept new data on any clock cycle, so it is always ready.
Benchmark Block Latency from Simulation
To verify the block latency equations, log the ready/valid handshake signals to measure the block latency in simulation.
validInHistoryShared = out.validInShared; readyHistoryShared = out.readyShared; validOutHistoryShared = out.validOutShared; readyInHistoryShared = out.readyInShared; validInHistoryPipelined = out.validInPipelined; readyHistoryPipelined = out.readyPipelined; validOutHistoryPipelined = out.validOutPipelined; readyInHistoryPipelined = out.readyInPipelined;
CORDIC Square Root Resource-Shared Block Latency
Find the data transaction time for the CORDIC Square Root Resource-Shared block.
tDataInShared = find(validInHistoryShared & readyHistoryShared == 1); tDataOutShared = find(validOutHistoryShared & readyInHistoryShared == 1);
Find the rising edge of the ready signal.
tReadyShared = find(diff(readyHistoryShared) == 1) + 1;
Compute the block latency from a successful input to the output.
blockLatencySharedSim = tDataOutShared - tDataInShared(1:numSamples)
blockLatencySharedSim = 3×1
24
24
24
Compute the block latency from a successful output to when the block becomes ready again.
readyLatencySharedSim = tReadyShared - tDataOutShared
readyLatencySharedSim = 3×1
1
1
1
CORDIC Square Root Fully-Pipelined Block Latency
Find the data transaction time.
tDataInPipelined = find(validInHistoryPipelined & readyHistoryPipelined == 1); tDataOutPipelined = find(validOutHistoryPipelined & readyInHistoryPipelined == 1);
Compute the block latency from a successful into to the corresponding output.
blockLatencyPipelinedSim = tDataOutPipelined(1:numSamples) - tDataInPipelined(1:numSamples)
blockLatencyPipelinedSim = 3×1
23
23
23
Hardware Resource Utilization
Both blocks in this example support HDL code generation using the Simulink® HDL Workflow Advisor. For an example, see HDL Code Generation and FPGA Synthesis from Simulink Model (HDL Coder)(HDL Coder) and Implement Digital Downconverter for FPGA (HDL Coder) (DSP HDL Toolbox).
This example data was generated by synthesizing the block on a Xilinx® Zynq®-7000 SoC ZC702 Evaluation Kit. The synthesis tool was Vivado® v2022.1 (win64).
These parameters were used for synthesis:
Input data type:
sfix16_En10maximumShiftValue: 15 (WordLength - 1)Target frequency: 200 MHz
This table shows the post-place-and-route resource utilization results for the CORDIC Square Root Resource-Shared block.
Resource | Usage | Available | Utilization (%) |
Slice LUTs | 445 | 53200 | 0.84 |
Slice Registers | 92 | 106400 | 0.09 |
DSPs | 0 | 220 | 0.00 |
Block RAM Tile | 0 | 140 | 0.00 |
This table shows the timing summary for the CORDIC Square Root Resource-Shared block.
Value | |
Requirement | 5 ns (200 MHz) |
Data Path Delay | 5.337 ns |
Slack | -0.312 ns |
Clock Frequency | 184.71 MHz |
This table shows the post-place-and-route resource utilization results for the CORDIC Square Root Fully-Pipelined block.
Resource | Usage | Available | Utilization (%) |
Slice LUTs | 926 | 53200 | 1.74 |
Slice Registers | 701 | 106400 | 0.66 |
DSPs | 0 | 220 | 0.00 |
Block RAM Tile | 0 | 140 | 0.00 |
This table shows the timing summary for the CORDIC Square Root Fully-Pipelined block.
Value | |
Requirement | 5 ns (200 MHz) |
Data Path Delay | 5.016 ns |
Slack | 0.009 ns |
Clock Frequency | 200.36 MHz |
See Also
CORDIC Square Root HDL Optimized