ルックアップ テーブルを使用した固定小数点 Log2 の実装
この例では、ルックアップ テーブルを使用して固定小数点 log2 を実装する方法を説明します。ルックアップ テーブルを使用すると、組み込みデバイス用にコードを効率的に生成できます。
Log2 アルゴリズム
ここでは、以下の関数 fi_log2lookup_8_bit_byte によって実装される log2 アルゴリズムの概要をまとめます。
1 バイトのビット数を定数
Bとして宣言します。この例では、B=8となります。ルックアップ テーブルのデータの正規化の例で説明されている関数
fi_normalize_unsigned_8_bit_byte()を使用して、u = x*2^nおよび1 <= x < 2となるように、入力u>0を正規化します。xの上位Bビットを抽出します。x_Bは、xの上位Bビットを示します。log2(x_B)がインデックスlog2(x_B) = LOG2LUT(i)を検索して実行できるよう、整数i = x_B - 2^(B-1) + 1が LOG2LUT へのインデックスとして使用されるルックアップ テーブル LOG2LUT を生成します。小数部として解釈されている残りのビット
r = x - x_Bを使用して、tableLOG2LUT(i+1)のLOG2LUT(i)と次の値の間で線形内挿を行います。残りのビットrはxの下位w - Bビットを抽出して作成します。ここで、wはxの語長を示します。関数reinterpretcast()を使用すると、これは小数部として解釈されます。最後に、ルックアップ テーブルと線形内挿を使用して、次のように出力を計算します。
log2(u) = log2(x*2^n)
= n + log2(x)
= n + LOG2LUT(i) + r*(LOG2LUT(i+1) - LOG2LUT(i))
ルックアップ テーブルを使用した固定小数点 Log2 の計算
fi_log2lookup_8_bit_byte() により、ルックアップ テーブルを使用して固定小数点 log2 を計算します。固定小数点ルックアップ テーブルの結果を、log2 および倍精度で計算された対数と比較します。
u = fi(linspace(0.001,20,100)); y = fi_log2lookup_8_bit_byte(u); y_expected = log2(double(u));
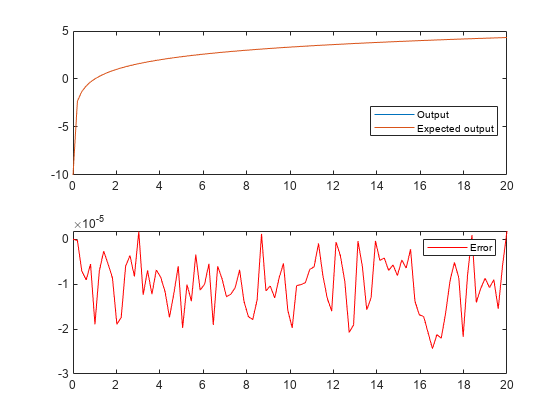
結果をプロットします。
clf subplot(211) plot(u,y,u,y_expected) legend('Output','Expected output','Location','Best') subplot(212) plot(u,double(y)-y_expected,'r') legend('Error')
figure(gcf)
fi_log2lookup_8_bit_byte の関数定義
function y = fi_log2lookup_8_bit_byte(u) % Load the lookup table LOG2LUT = log2_lookup_table(); % Remove fimath from the input to insulate this function from math % settings declared outside this function. u = removefimath(u); % Declare the output y = coder.nullcopy(fi(zeros(size(u)),numerictype(LOG2LUT),fimath(LOG2LUT))); B = 8; % Number of bits in a byte w = u.WordLength; for k = 1:numel(u) assert(u(k)>0,'Input must be positive.'); % Normalize the input such that u = x*2^n and 1 <= x < 2 [x,n] = fi_normalize_unsigned_8_bit_byte(u(k)); % Extract the high byte of x high_byte = storedInteger(bitsliceget(x, w, w - B + 1)); % Convert the high byte into an index for LOG2LUT i = high_byte - 2^(B-1) + 1; % Interpolate between points. % The upper byte was used for the index into LOG2LUT % The remaining bits make up the fraction between points. T_unsigned_fraction = numerictype(0, w-B, w-B); r = reinterpretcast(bitsliceget(x,w-B,1), T_unsigned_fraction); y(k) = n + LOG2LUT(i) + ... r*(LOG2LUT(i+1) - LOG2LUT(i)) ; end % Remove fimath from the output to insulate the caller from math settings % declared inside this function. y = removefimath(y); end
Log2 ルックアップ テーブル
関数 log2_lookup_table は、値 log2 のルックアップ テーブルを読み込みます。テーブルは次を実行すると作成できます。
B = 8;
log2_table = log2((2^(B-1):2^(B))/2^(B-1))
function LOG2LUT = log2_lookup_table() B = 8; % Number of bits in a byte % log2_table = log2((2^(B-1) : 2^(B)) / 2^(B - 1)) log2_table = [0.000000000000000 0.011227255423254 0.022367813028454 0.033423001537450 ... 0.044394119358453 0.055282435501190 0.066089190457773 0.076815597050831 ... 0.087462841250339 0.098032082960527 0.108524456778169 0.118941072723507 ... 0.129283016944966 0.139551352398794 0.149747119504682 0.159871336778389 ... 0.169925001442312 0.179909090014934 0.189824558880017 0.199672344836364 ... 0.209453365628950 0.219168520462162 0.228818690495881 0.238404739325079 ... 0.247927513443586 0.257387842692652 0.266786540694901 0.276124405274238 ... 0.285402218862248 0.294620748891627 0.303780748177103 0.312882955284355 ... 0.321928094887362 0.330916878114617 0.339850002884625 0.348728154231078 ... 0.357552004618084 0.366322214245816 0.375039431346925 0.383704292474052 ... 0.392317422778760 0.400879436282184 0.409390936137702 0.417852514885898 ... 0.426264754702098 0.434628227636725 0.442943495848728 0.451211111832329 ... 0.459431618637297 0.467605550082997 0.475733430966398 0.483815777264256 ... 0.491853096329675 0.499845887083205 0.507794640198696 0.515699838284042 ... 0.523561956057013 0.531381460516312 0.539158811108031 0.546894459887637 ... 0.554588851677637 0.562242424221073 0.569855608330948 0.577428828035749 ... 0.584962500721156 0.592457037268080 0.599912842187128 0.607330313749611 ... 0.614709844115208 0.622051819456376 0.629356620079610 0.636624620543649 ... 0.643856189774725 0.651051691178929 0.658211482751795 0.665335917185176 ... 0.672425341971496 0.679480099505446 0.686500527183218 0.693486957499325 ... 0.700439718141092 0.707359132080883 0.714245517666123 0.721099188707185 ... 0.727920454563199 0.734709620225838 0.741466986401147 0.748192849589460 ... 0.754887502163469 0.761551232444479 0.768184324776926 0.774787059601173 ... 0.781359713524660 0.787902559391432 0.794415866350106 0.800899899920305 ... 0.807354922057604 0.813781191217037 0.820178962415188 0.826548487290915 ... 0.832890014164742 0.839203788096944 0.845490050944375 0.851749041416058 ... 0.857980995127572 0.864186144654280 0.870364719583405 0.876516946565000 ... 0.882643049361841 0.888743248898259 0.894817763307943 0.900866807980749 ... 0.906890595608518 0.912889336229962 0.918863237274595 0.924812503605781 ... 0.930737337562886 0.936637939002571 0.942514505339240 0.948367231584678 ... 0.954196310386875 0.960001932068081 0.965784284662087 0.971543553950772 ... 0.977279923499916 0.982993574694310 0.988684686772166 0.994353436858858 ... 1.000000000000000]; % Cast to fixed point with the most accurate rounding method WL = 4*B; % Word length FL = 2*B; % Fraction length LOG2LUT = fi(log2_table,1,WL,FL,'RoundingMethod','Nearest'); % Set fimath for the most efficient math operations F = fimath('OverflowAction','Wrap',... 'RoundingMethod','Floor',... 'SumMode','SpecifyPrecision',... 'SumWordLength',WL,... 'SumFractionLength',FL,... 'ProductMode','SpecifyPrecision',... 'ProductWordLength',WL,... 'ProductFractionLength',2*FL); LOG2LUT = setfimath(LOG2LUT,F); end
You can also select a web site from the following list:
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)