正弦関数のルックアップ テーブルの作成
はじめに
以下の節では、関数 fixpt_look1_func_approx を使用してルックアップ テーブルを作成する方法を説明します。区間 0 ~ 0.25 にある関数 sin(2πx) のルックアップ テーブルを作成する方法の例を紹介します。
ルックアップ テーブルの関数パラメーターの設定
まず、関数 fixpt_look1_func_approx のパラメーター値を定義します。
% Required parameters funcstr = 'sin(2*pi*x)'; % Ideal function xmin = 0; % Minimum input of interest xmax = 0.25; % Maximum input of interest xdt = ufix(16); % x data type xscale = 2^-16; % x data scaling ydt = sfix(16); % y data type yscale = 2^-14; % y data scaling rndmeth = 'Floor'; % Rounding method % Optional parameters errmax = 2^-10; % Maximum allowed error of the lookup table nptsmax = 21; % Maximum number of points of the lookup table
パラメーター errmax、nptsmax、spacing はオプションです。少なくとも errmax または nptsmax のいずれかのパラメーターを使用しなければなりません。errmax パラメーターのみを使用し、nptsmax を使用しない場合、関数は点が最も少ないルックアップ テーブルを作成し、最悪誤差は最大で errmax になります。nptsmax パラメーターのみを使用し、errmax を使用しない場合、関数は最大 nptsmax の点があるルックアップ テーブルを作成し、最悪誤差は最小になります。オプションの spacing パラメーターを使用して、ルックアップ テーブルのブレークポイント間の間隔を制限できます。
制限のない間隔で errmax を使用する
指定した最悪誤差のデータ点が最も少ないルックアップ テーブルを間隔を制限せずに作成します。
[xdata,ydata,errworst] = fixpt_look1_func_approx(funcstr, ...
xmin,xmax,xdt,xscale,ydt,yscale,rndmeth,errmax,[]);nptsmax パラメーターと spacing パラメーターは指定されていないことに注意してください。
length(xdata)
ans = 16
を errmax で指定される許容誤差内に近似するには、16 個の点が必要です。最大誤差は以下のようになります。
errworst
errworst = 9.7656e-04
errworst の値は、errmax の値以下になります。
結果をプロットします。
figure(1)
fixpt_look1_func_plot(xdata,ydata,funcstr,xmin,xmax,xdt, ...
xscale,ydt,yscale,rndmeth);
上のプロットは、理想関数 とブレークポイント間の固定小数点ルックアップ テーブル近似を示します。この例では、理想関数と近似が非常に近接しているため 2 つのグラフは一致しているように見えます。下のプロットは誤差を示します。
この例では、Y データ点 ydata が xdata の点に適用された理想関数と等しくなっています。ただし、fixpt_look1_func_approx を実行すると ydata に別の値のセットを定義することができます。これにより最大誤差が小さくなる場合があります。
また、元の区間のサブセットのルックアップ テーブルを評価するために、xmin と xmax の値を変えることもできます。
ydata、xmin、または xmax を変更した後の新しい最大誤差を確認するには、以下のように入力します。
errworst = fixpt_look1_func_plot(xdata,ydata,funcstr,xmin,xmax,xdt,xscale,ydt,yscale,rndmeth)
制限のない間隔で nptsmax を使用する
指定した最大データ点数の最悪誤差を最小にするルックアップ テーブルを間隔を制限せずに作成します。
[xdata, ydata, errworst] = fixpt_look1_func_approx(funcstr, ...
xmin,xmax,xdt,xscale,ydt,yscale,rndmeth,[],nptsmax);空の大かっこは、この例では使用しないパラメーター errmax を無視するように関数に伝えます。errmax を省略すると、関数は nptsmax で指定されたサイズの、最悪誤差の最も小さいルックアップ テーブルを返します。
length(xdata)
ans = 21
関数は 21 個の点があるベクトル xdata を返します。最大誤差は以下のようになります。
errworst
errworst = 5.1139e-04
errworst の値は、errmax の値以下になります。
結果をプロットします。
figure(2)
fixpt_look1_func_plot(xdata,ydata,funcstr,xmin,xmax,xdt, ...
xscale,ydt,yscale,rndmeth);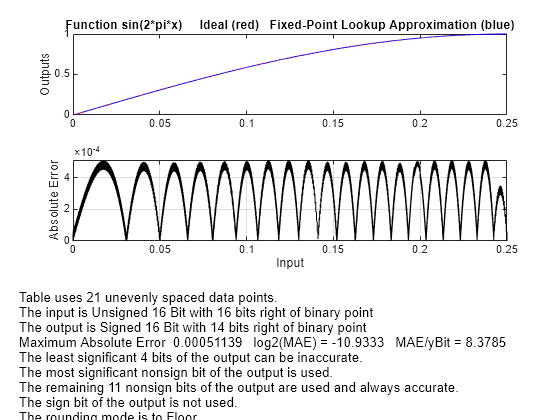
間隔の制限
上記の 2 つの例では、関数 fixpt_look1_func_approx は点の間隔を制限しないルックアップ テーブルを作成します。間隔パラメーターを使用し、間隔を制限してルックアップ テーブルの計算効率を高めることができます。2 のべき乗間隔 'pow2' と等間隔 'even' は両方ともルックアップ テーブルの計算速度を向上させ、コマンドの読み取り専用メモリ (ROM) の使用量が少なくします。ただし、いずれかの間隔制限を errmax と一緒に指定すると、同程度の精度を実現するために、通常は間隔を制限しない場合よりもデータ点が多く必要になります。詳細については、速度、誤差、およびメモリの使用量に与える間隔の影響を参照してください。
等間隔で errmax を使用する
ブレークポイントが等間隔で、最悪誤差が指定されているルックアップ テーブルを作成します。
spacing = 'even'; [xdata,ydata,errworst] = fixpt_look1_func_approx(funcstr, ... xmin,xmax,xdt,xscale,ydt,yscale,rndmeth,errmax,[],spacing); length(xdata)
ans = 20
errworst
errworst = 9.2109e-04
結果をプロットします。
figure(3)
fixpt_look1_func_plot(xdata,ydata,funcstr,xmin,xmax,xdt, ...
xscale,ydt,yscale,rndmeth);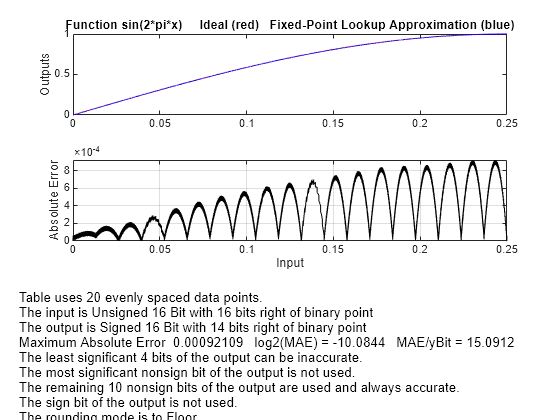
等間隔で nptsmax を使用する
ブレークポイントが等間隔で、指定された最大数の点の最悪誤差を最小にするルックアップ テーブルを作成します。
spacing = 'even'; [xdata, ydata, errworst] = fixpt_look1_func_approx(funcstr, ... xmin,xmax,xdt,xscale,ydt,yscale,rndmeth,[],nptsmax,spacing); length(xdata)
ans = 21
errworst
errworst = 8.3793e-04
結果は、2^-10.2209 の最大絶対誤差を実現するためには 21 個の等間隔の点が必要です。
結果をプロットします。
figure(4)
fixpt_look1_func_plot(xdata,ydata,funcstr,xmin,xmax,xdt, ...
xscale,ydt,yscale,rndmeth);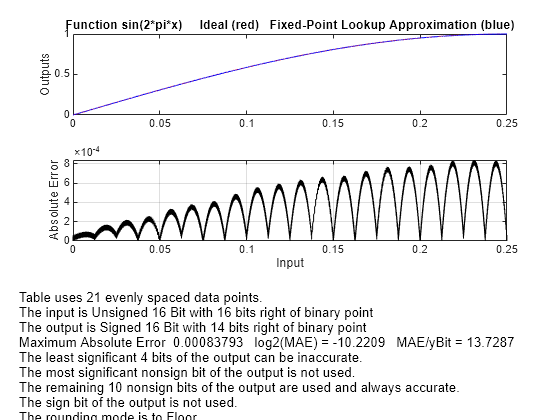
2 のべき乗の間隔で errmax を使用する
間隔が 2 のべき乗で、最悪誤差が指定されているルックアップ テーブルを作成します。
spacing = 'pow2'; [xdata, ydata, errworst] = ... fixpt_look1_func_approx(funcstr,xmin, ... xmax,xdt,xscale,ydt,yscale,rndmeth,errmax,[],spacing); length(xdata)
ans = 33
errmax で指定した最悪誤差を実現するには、33 個の点が必要です。これらの点が等間隔であることを検証するには、以下のように入力します。
widths = diff(xdata)
widths = 32×1
0.0078
0.0078
0.0078
0.0078
0.0078
0.0078
0.0078
0.0078
0.0078
0.0078
0.0078
0.0078
0.0078
0.0078
0.0078
⋮
これは、要素が xdata 内の連続する点間の差であるベクトルを生成します。widths のすべての要素は 2^-7 です。
最大誤差は以下のようになります。
errworst
errworst = 3.7209e-04
これは、errmax の値以下です。
結果をプロットします。
figure(5)
fixpt_look1_func_plot(xdata,ydata,funcstr,xmin,xmax,xdt, ...
xscale,ydt,yscale,rndmeth);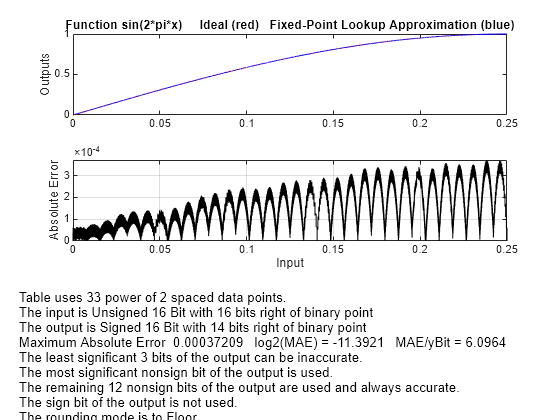
2 のべき乗の間隔で nptsmax を使用する
間隔が 2 のべき乗で、指定された数の点の最悪誤差を最小にするルックアップ テーブルを作成します。
spacing = 'pow2'; [xdata, ydata, errworst] = ... fixpt_look1_func_approx(funcstr,xmin, ... xmax,xdt,xscale,ydt,yscale,rndmeth,[],nptsmax,spacing); length(xdata)
ans = 17
errworst
errworst = 0.0013
最大絶対誤差 2^-9.6267 を達成するには 17 個の点が必要です。
結果をプロットします。
figure(6)
fixpt_look1_func_plot(xdata,ydata,funcstr,xmin,xmax,xdt, ...
xscale,ydt,yscale,rndmeth);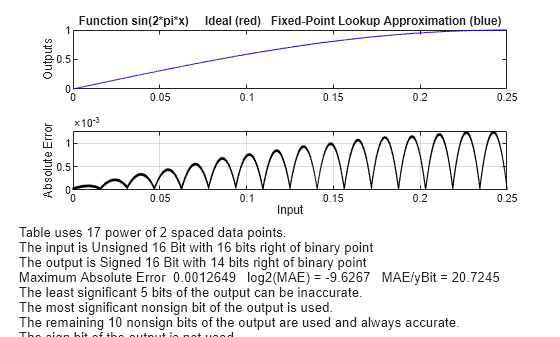
errmax と nptsmax の両方を指定する
errmax パラメーターと nptsmax パラメーターの両方を含めると、関数 fixpt_look1_func_approx はデータ点が最大 nptsmax 個で、最悪誤差が最大 errmax のルックアップ テーブルを見つけます。両方の条件を満たすルックアップ テーブルを見つけた場合、間隔に次の優先順位が使用されます。
2 のべき乗
偶数
制限がない
関数が両方の条件を満たすルックアップ テーブルを見つけられない場合、nptsmax は無視され、間隔に制限がなく最悪誤差が最大で errmax のルックアップ テーブルが返されます。この場合、関数は nptsmax パラメーターが省略されたときと同じ動作をします。
次の例は、以下のように入力するときに nptsmax に別の値を指定した場合の結果を示します。
[xdata ydata errworst] = fixpt_look1_func_approx(funcstr, ... xmin,xmax,xdt,xscale,ydt,yscale,rndmeth,errmax,nptsmax);
nptsmax の 3 つの異なる設定の結果は次のとおりです。
nptsmax = 33;— 例 3 のように、関数は間隔が 2 のべき乗の 33 個の点があるルックアップ テーブルを作成します。nptsmax = 21;— 例 5 のように、errmaxとnptsmaxの条件は 2 のべき乗の間隔では満たされないため、関数は等間隔の 20 個の点があるルックアップ テーブルを作成します。nptsmax = 16;— 例 1 のように、errmaxとnptsmaxの条件は 2 のべき乗の間隔でも等間隔でも満たされないため、関数は間隔に制限のない 16 個の点があるルックアップ テーブルを作成します。
例の結果の比較
次の表では、例の結果をまとめます。errmax を指定すると、等間隔では間隔に制限がない場合よりも多くのデータ点が必要になり、2 のべき乗の間隔では等間隔の場合よりも多くの点が必要になります。
| 例 | オプション | 間隔 | 最悪誤差 | テーブル内の点数 |
|---|---|---|---|---|
1 |
|
|
| 16 |
2 |
|
|
| 21 |
3 |
|
|
| 20 |
4 |
|
|
| 21 |
5 |
|
|
| 33 |
6 |
|
|
| 17 |