算術演算

メモ

以下の節は、どのデータ型とスケーリングを選択するとオーバーフローや精度の低下が発生するかを理解するのに役立ちます。

モジュロ演算

2 進数はモジュロ演算に基づきます。モジュロ演算は有限数値セットのみを使用して、そのセットの範囲外となる計算結果をラップしてセット内に戻します。

たとえば、日常的な時計はモジュロ 12 演算を使用しています。このシステムの数字は 1 ～ 12 のみなので、"時計" システムで 9 足す 9 は 6 です。これは数値円として容易に可視化できます。

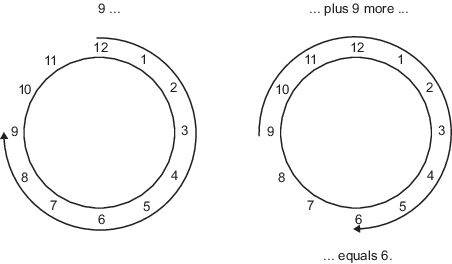
同様に、2 進数では 0 と 1 しか使用できないので、この範囲外となる演算結果は "円を周って" 0 または 1 にラップされます。

2 の補数

2 の補数は 2 進数を解釈する方法の 1 つです。2 の補数では、正の数値が常に 0 から始まり、負の数値が常に 1 から始まります。2 の補数の最初のビットが 0 の場合、値は標準的な 2 進数の値を計算して得られます。2 の補数の最初のビットが 1 の場合、値は左端のビットが負であると想定し、2 進数の値を計算して得られます。以下に例を示します。

$\begin{array}{l} 01 = (0 + 2^{0}) = 1 \\ 11 = ((- 2^{1}) + (2^{0})) = (- 2 + 1) = - 1 \end{array}$

2 の補数を使用して負の 2 進数を計算するには、次のようにします。

1 の補数を取るか、"ビットを反転" します。
2 進数を使用して 2^(-FL) を追加します。ここで FL は小数部の長さです。
元の語長を超えたビットは破棄します。

たとえば、11010 (-6) の負を取ることにします。まず、この数値の 1 の補数を取るか、次のようにビットを反転します。

$11010 \to 00101$

次に、1 を足してすべての数値を 0 か 1 にラップします。

$\begin{array}{l} \underline{\begin{array}{r} 00101 \\ + 1 \end{array}} \\ \begin{matrix} 00110 & (6) \end{matrix} \end{array}$

加算と減算

固定小数点数の加算では、加数の 2 進小数点を整列する必要があります。次に、0 または 1 以外の数値が使用されないように、2 進数を使用して加算を実行します。

たとえば、010010.1 (18.5) と 0110.110 (6.75) を加算します。

$\begin{matrix} \begin{array}{r} \underline{\begin{matrix} 010010.1 \\ + 0110.110 \end{matrix}} \\ 011001.010 \end{array} & \begin{array}{l} (18.5) \\ (6.75) \\ (25.25) \end{array} \end{matrix}$

固定小数点の減算は加算と同じですが、負の値に 2 の補数を使用します。減算では、加数を符号拡張して相互の長さを一致させなければなりません。たとえば、010010.1 (18.5) から 0110.110 (6.75) を減算します。

$\begin{matrix} \underline{\begin{matrix} 010010.100 \\ - 0110.110 \end{matrix}} & \begin{matrix} (18.5) \\ (6.75) \end{matrix} \end{matrix}$

既定の fimath では、CastBeforeSum プロパティの値は 1 (true) です。これによって加算の前に、加数が加算データ型にキャストされます。したがって、加算中に 2 進小数点を揃えるためのシフトは不要です。

CastBeforeSum の値が 0 (偽) の場合は、加数が完全精度を維持して加算されます。加算後に和が量子化されます。

乗算

2 の補数固定小数点数の乗算は通常の 10 進法の乗算と類似していますが、中間結果を加算する前に符号拡張して左側を揃えなければならない点が異なります。

たとえば、10.11 (-1.25) と 011 (3) を乗算します。

乗算のデータ型

以下の図は、Fixed-Point Designer™ ソフトウェアで固定小数点の乗算に使用されるデータ型を示しています。これらの図は、実数と実数、複素数と実数、複素数と複素数の乗算に使用されるデータ型の違いを説明しています。

実数と実数の乗算. 次の図は、2 つの実数の乗算でツールボックスが使用するデータ型を示しています。ソフトウェアはこの演算の出力を乗算データ型で返します。これは fimath オブジェクトの ProductMode プロパティによって決まります。

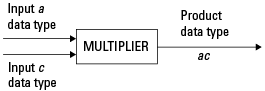
実数と複素数の乗算. 次の図は、実数と複素数の固定小数点数の乗算でツールボックスが使用するデータ型を示しています。実数と複素数の乗算と、複素数と実数の乗算は等価です。ソフトウェアはこの演算の出力を乗算データ型で返します。これは fimath オブジェクトの ProductMode プロパティによって決まります。

複素数と複素数の乗算. 次の図は、2 つの複素数固定小数点数の乗算を示しています。ソフトウェアはこの演算の出力を加算データ型で返します。これは fimath オブジェクトの SumMode プロパティによって決まります。中間の乗算データ型は fimath オブジェクトの ProductMode プロパティによって決まります。

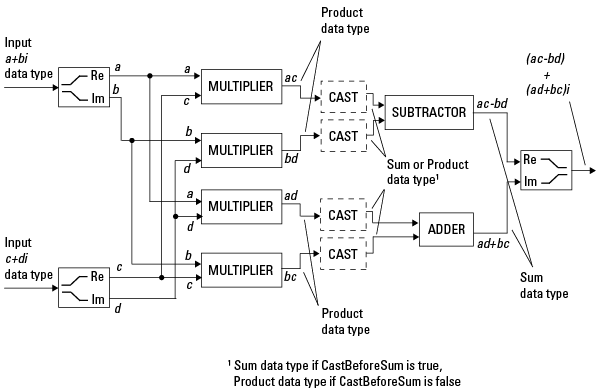
fimath オブジェクトの CastBeforeSum プロパティが true の場合、前の図では乗数の後に加算データ型へのキャストが発生しています。C コードでは、これは以下に相当します。

acc=ac;
acc-=bd;

上記は減算の場合です。

acc=ad;
acc+=bc;

これは加算の場合で、acc はアキュムレータです。CastBeforeSum プロパティが false の場合は、減算と加算の演算の前にキャストが発生せず、データは乗算データ型のままです。

fimath を使用する乗算

次の例を見てみましょう。

F = fimath('ProductMode','FullPrecision',...
'SumMode','FullPrecision');
T1 = numerictype('WordLength',24,'FractionLength',20);
T2 = numerictype('WordLength',16,'FractionLength',10);

実数*実数. 結果 z の語長と小数部の長さは、それぞれ被乗数の語長と小数部の長さの和と等しくなります。これは、fimath SumMode プロパティと ProductMode プロパティが FullPrecision に設定されているからです。

P = fipref;
P.FimathDisplay = 'none';
x = fi(5,T1,F)

x = 

     5

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 24
        FractionLength: 20

y = fi(10,T2,F)

y = 

    10

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 10

z = x*y

z = 

    50

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 40
        FractionLength: 30

実数*複素数. 結果 z の語長と小数部の長さは、それぞれ被乗数の語長と小数部の長さの和と等しくなります。これは、fimath SumMode プロパティと ProductMode プロパティが FullPrecision に設定されているからです。

x = fi(5,T1,F)

x = 

     5

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 24
        FractionLength: 20

y = fi(10+2i,T2,F)

y = 

  10.0000 + 2.0000i

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 10

z = x*y

z = 

  50.0000 +10.0000i

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 40
        FractionLength: 30

複素数*複素数. 複素数と複素数の乗算には、乗算だけでなく加算も必要になります。その結果、最大精度の結果の語長は被乗数の語長の和より 1 ビット多くなります。

x = fi(5+6i,T1,F)

x = 

   5.0000 + 6.0000i

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 24
        FractionLength: 20

y = fi(10+2i,T2,F)

y = 

  10.0000 + 2.0000i

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 10

z = x*y

z = 

  38.0000 +70.0000i

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 41
        FractionLength: 30

キャスト

fimath オブジェクトでは、中間積加算データ型とスケーリングを SumMode プロパティと ProductMode プロパティで指定できます。SumMode プロパティと ProductMode プロパティを設定するときには、各キャストの影響に注意してください。選択したデータ型によっては、オーバーフローや丸めが生じる可能性があります。次の 2 つの例は、オーバーフローと丸めが発生する状況を示しています。

メモ

キャストのその他の例は、fi オブジェクトのキャストを参照してください。

短いデータ型から長いデータ型へのキャスト

小数部が 2 ビットの 4 ビットデータ型から、小数部が 7 ビットの 8 ビットデータ型への非ゼロ数値のキャストを考えてみます。

図のように、2 進小数点がキャスト先の 2 進小数点の位置と一致するように、ソースビットが左にシフトします。最上位のソースビットがあふれるため、オーバーフローが発生する可能性があり、結果は飽和またはラップします。キャスト先データ型の末端にある空のビットは 0 または 1 で埋められます。

オーバーフローが発生しない場合は、空のビットが 0 で埋められます。
ラップが発生した場合は、空のビットが 0 で埋められます。
飽和が発生した場合は、以下の処理が行われます。
- 正の数値の空のビットは 1 で埋められます。
- 負の数値の空のビットは 0 で埋められます。

短いデータ型から長いデータ型へのキャストを使用しても、オーバーフローが発生することがわかります。これは、ソースデータ型の整数の長さ (この場合は 2) が、キャスト先データ型 (この場合は 1) の整数の長さより長いときに起こることがあります。同様に、短いデータ型から長いデータ型にキャストするときでも、キャスト先のデータ型とスケーリングの小数ビット数がソースよりも少ない場合は、丸めが必要になることがあります。

長いデータ型から短いデータ型へのキャスト

小数部が 7 ビットの 8 ビットデータ型から、小数部が 2 ビットの 4 ビットデータ型への非ゼロ数値のキャストを考えてみます。

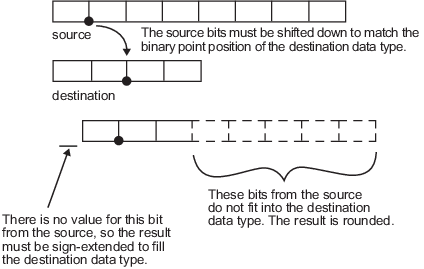
図のように、2 進小数点がキャスト先の 2 進小数点の位置と一致するように、ソースビットが右にシフトします。ソースからの最上位ビットの値はないので、符号拡張を使用してキャスト先データ型の整数部を指定します。符号拡張とは、最上位ビットの値をもつビットを 2 の補数値の最上部に追加することです。符号拡張は 2 進数の値を変更しません。この例では、ソースの下位 5 ビットはキャスト先の小数部の長さに収まりません。したがって、結果は丸められるので精度が低下する可能性があります。

この場合は、長いデータ型から短いデータ型へのキャストでも、すべての整数ビットが維持されます。一方、短いデータ型にキャストする場合でも、キャスト先データ型の小数部の長さがソースデータ型の小数部の長さ以上の場合は、完全精度を維持できます。ただし、その場合は結果の最上位からビットが失われ、オーバーフローが発生する可能性があります。

最悪の状況は、キャスト先データ型の整数の長さと小数部の長さが、ソースのデータ型とスケーリングの整数の長さと小数部の長さよりも短い場合に発生します。その場合は、オーバーフローと精度低下の両方が起こる可能性があります。