Fit a VEC(1) model to seven macroeconomic series. Supply the response data as a numeric matrix.
Consider a VEC model for the following macroeconomic series:
Gross domestic product (GDP)
GDP implicit price deflator
Paid compensation of employees
Nonfarm business sector hours of all persons
Effective federal funds rate
Personal consumption expenditures
Gross private domestic investment
Suppose that a cointegrating rank of 4 and one short-run term are appropriate, that is, consider a VEC(1) model.
Load the Data_USEconVECModel data set.
For more information on the data set and variables, enter Description at the command line.
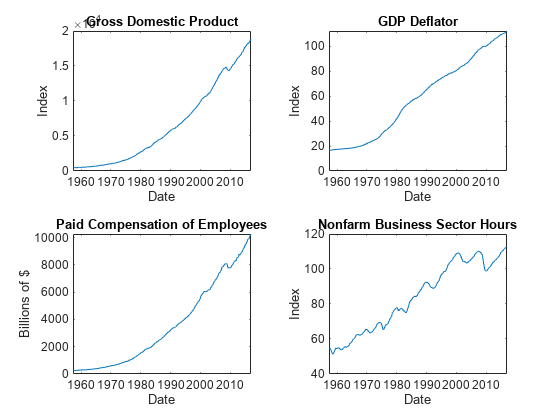
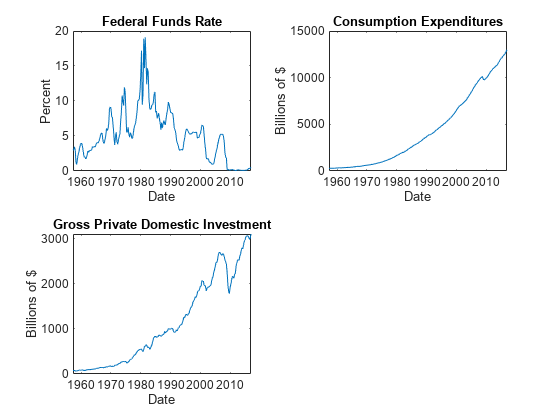
Determine whether the data needs to be preprocessed by plotting the series on separate plots.
Stabilize all series, except the federal funds rate, by applying the log transform. Scale the resulting series by 100 so that all series are on the same scale.
Create a VEC(1) model using the shorthand syntax. Specify the variable names.
Mdl =
vecm with properties:
Description: "7-Dimensional Rank = 4 VEC(1) Model with Linear Time Trend"
SeriesNames: "GDP" "GDPDEF" "COE" ... and 4 more
NumSeries: 7
Rank: 4
P: 2
Constant: [7×1 vector of NaNs]
Adjustment: [7×4 matrix of NaNs]
Cointegration: [7×4 matrix of NaNs]
Impact: [7×7 matrix of NaNs]
CointegrationConstant: [4×1 vector of NaNs]
CointegrationTrend: [4×1 vector of NaNs]
ShortRun: {7×7 matrix of NaNs} at lag [1]
Trend: [7×1 vector of NaNs]
Beta: [7×0 matrix]
Covariance: [7×7 matrix of NaNs]
Mdl is a vecm model object. All properties containing NaN values correspond to parameters to be estimated given data.
Estimate the model using the entire data set and the default options.
EstMdl =
vecm with properties:
Description: "7-Dimensional Rank = 4 VEC(1) Model"
SeriesNames: "GDP" "GDPDEF" "COE" ... and 4 more
NumSeries: 7
Rank: 4
P: 2
Constant: [14.1329 8.77841 -7.20359 ... and 4 more]'
Adjustment: [7×4 matrix]
Cointegration: [7×4 matrix]
Impact: [7×7 matrix]
CointegrationConstant: [-28.6082 -109.555 77.0912 ... and 1 more]'
CointegrationTrend: [4×1 vector of zeros]
ShortRun: {7×7 matrix} at lag [1]
Trend: [7×1 vector of zeros]
Beta: [7×0 matrix]
Covariance: [7×7 matrix]
EstMdl is an estimated vecm model object. It is fully specified because all parameters have known values. By default, estimate imposes the constraints of the H1 Johansen VEC model form by removing the cointegrating trend and linear trend terms from the model. Parameter exclusion from estimation is equivalent to imposing equality constraints to zero.
Display a short summary from the estimation.
results = struct with fields:
Description: "7-Dimensional Rank = 4 VEC(1) Model"
Model: "H1"
SampleSize: 238
NumEstimatedParameters: 112
LogLikelihood: -1.4939e+03
AIC: 3.2118e+03
BIC: 3.6007e+03
Table: [133×4 table]
Covariance: [7×7 double]
Correlation: [7×7 double]
The Table field of results is a table of parameter estimates and corresponding statistics.