simulate
Monte Carlo simulation of vector error-correction (VEC) model
Syntax
Description
Conditional and Unconditional Simulation for Numeric Arrays
Y = simulate(Mdl,numobs,Name=Value)simulate returns numeric arrays when all optional
input data are numeric arrays. For example,
simulate(Mdl,100,NumPaths=1000,Y0=PS) returns a numeric
array of 1000, 100-period simulated response paths from Mdl
and specifies the numeric array of presample response data
PS.
To perform a conditional simulation, specify response data in the simulation
horizon by using the YF name-value argument.
Unconditional Simulation for Tables and Timetables
Tbl = simulate(Mdl,numobs,Presample=Presample)Tbl containing the random
multivariate response and innovations variables, which results from the
unconditional simulation of the response series in the model
Mdl. simulate uses the table or
timetable of presample data Presample to initialize the
response series. (since R2022b)
simulate selects the variables in
Mdl.SeriesNames to simulate or all variables in
Presample. To select different response variables in
Presample to simulate, use the
PresampleResponseVariables name-value argument.
Tbl = simulate(Mdl,numobs,Presample=Presample,Name=Value)simulate(Mdl,100,Presample=PSTbl,PresampleResponseVariables=["GDP"
"CPI"]) returns a timetable of variables containing 100-period
simulated response and innovations series from Mdl,
initialized by the data in the GDP and CPI
variables of the timetable of presample data in PSTbl. (since R2022b)
Conditional Simulation for Tables and Timetables
Tbl = simulate(Mdl,numobs,InSample=InSample,ResponseVariables=ResponseVariables)Tbl containing the random
multivariate response and innovations variables, which results from the
conditional simulation of the response series in the model
Mdl. InSample is a table or
timetable of response or predictor data in the simulation horizon that
simulate uses to perform the conditional simulation
and ResponseVariables specifies the response variables in
InSample. (since R2022b)
Tbl = simulate(___,Name=Value)
Examples
Consider a VEC model for the following seven macroeconomic series, fit the model to the data, and then perform unconditional simulation by generating a random path of the response variables from the estimated model.
Gross domestic product (GDP)
GDP implicit price deflator
Paid compensation of employees
Nonfarm business sector hours of all persons
Effective federal funds rate
Personal consumption expenditures
Gross private domestic investment
Suppose that a cointegrating rank of 4 and one short-run term are appropriate, that is, consider a VEC(1) model.
Load the Data_USEconVECModel data set.
load Data_USEconVECModelFor more information on the data set and variables, enter Description at the command line.
Determine whether the data needs to be preprocessed by plotting the series on separate plots.
figure tiledlayout(2,2) nexttile plot(FRED.Time,FRED.GDP) title("Gross Domestic Product") ylabel("Index") xlabel("Date") nexttile plot(FRED.Time,FRED.GDPDEF) title("GDP Deflator") ylabel("Index") xlabel("Date") nexttile plot(FRED.Time,FRED.COE) title("Paid Compensation of Employees") ylabel("Billions of $") xlabel("Date") nexttile plot(FRED.Time,FRED.HOANBS) title("Nonfarm Business Sector Hours") ylabel("Index") xlabel("Date")
figure tiledlayout(2,2) nexttile plot(FRED.Time,FRED.FEDFUNDS) title("Federal Funds Rate") ylabel("Percent") xlabel("Date") nexttile plot(FRED.Time,FRED.PCEC) title("Consumption Expenditures") ylabel("Billions of $") xlabel("Date") nexttile plot(FRED.Time,FRED.GPDI) title("Gross Private Domestic Investment") ylabel("Billions of $") xlabel("Date")
Stabilize all series, except the federal funds rate, by applying the log transform. Scale the resulting series by 100 so that all series are on the same scale.
FRED.GDP = 100*log(FRED.GDP); FRED.GDPDEF = 100*log(FRED.GDPDEF); FRED.COE = 100*log(FRED.COE); FRED.HOANBS = 100*log(FRED.HOANBS); FRED.PCEC = 100*log(FRED.PCEC); FRED.GPDI = 100*log(FRED.GPDI);
Create a VECM(1) model using the shorthand syntax. Specify the variable names.
Mdl = vecm(7,4,1); Mdl.SeriesNames = FRED.Properties.VariableNames
Mdl =
vecm with properties:
Description: "7-Dimensional Rank = 4 VEC(1) Model with Linear Time Trend"
SeriesNames: "GDP" "GDPDEF" "COE" ... and 4 more
NumSeries: 7
Rank: 4
P: 2
Constant: [7×1 vector of NaNs]
Adjustment: [7×4 matrix of NaNs]
Cointegration: [7×4 matrix of NaNs]
Impact: [7×7 matrix of NaNs]
CointegrationConstant: [4×1 vector of NaNs]
CointegrationTrend: [4×1 vector of NaNs]
ShortRun: {7×7 matrix of NaNs} at lag [1]
Trend: [7×1 vector of NaNs]
Beta: [7×0 matrix]
Covariance: [7×7 matrix of NaNs]
Mdl is a vecm model object. All properties containing NaN values correspond to parameters to be estimated given data.
Estimate the model using the entire data set and the default options.
EstMdl = estimate(Mdl,FRED.Variables)
EstMdl =
vecm with properties:
Description: "7-Dimensional Rank = 4 VEC(1) Model"
SeriesNames: "GDP" "GDPDEF" "COE" ... and 4 more
NumSeries: 7
Rank: 4
P: 2
Constant: [14.1329 8.77841 -7.20359 ... and 4 more]'
Adjustment: [7×4 matrix]
Cointegration: [7×4 matrix]
Impact: [7×7 matrix]
CointegrationConstant: [-28.6082 -109.555 77.0912 ... and 1 more]'
CointegrationTrend: [4×1 vector of zeros]
ShortRun: {7×7 matrix} at lag [1]
Trend: [7×1 vector of zeros]
Beta: [7×0 matrix]
Covariance: [7×7 matrix]
EstMdl is an estimated vecm model object. It is fully specified because all parameters have known values. By default, estimate imposes the constraints of the H1 Johansen VEC model form by removing the cointegrating trend and linear trend terms from the model. Parameter exclusion from estimation is equivalent to imposing equality constraints to zero.
Simulate a response series path from the estimated model with length equal to the path in the data.
rng(1); % For reproducibility
numobs = size(FRED,1);
Y = simulate(EstMdl,numobs);Y is a 240-by-7 matrix of simulated responses. Columns correspond to the variable names in EstMdl.SeriesNames.
Illustrate the relationship between simulate and filter by estimating a 4-D VEC(1) model of the four response series in Johansen's Danish data set. Simulate a single path of responses using the fitted model and the historical data as initial values, and then filter a random set of Gaussian disturbances through the estimated model using the same presample responses.
Load Johansen's Danish economic data.
load Data_JDanishFor details on the variables, enter Description.
Create a default 4-D VEC(1) model. Assume that a cointegrating rank of 1 is appropriate.
Mdl = vecm(4,1,1); Mdl.SeriesNames = DataTable.Properties.VariableNames
Mdl =
vecm with properties:
Description: "4-Dimensional Rank = 1 VEC(1) Model with Linear Time Trend"
SeriesNames: "M2" "Y" "IB" ... and 1 more
NumSeries: 4
Rank: 1
P: 2
Constant: [4×1 vector of NaNs]
Adjustment: [4×1 matrix of NaNs]
Cointegration: [4×1 matrix of NaNs]
Impact: [4×4 matrix of NaNs]
CointegrationConstant: NaN
CointegrationTrend: NaN
ShortRun: {4×4 matrix of NaNs} at lag [1]
Trend: [4×1 vector of NaNs]
Beta: [4×0 matrix]
Covariance: [4×4 matrix of NaNs]
Estimate the VEC(1) model using the entire data set. Specify the H1* Johansen model form.
EstMdl = estimate(Mdl,Data,Model="H1*");When reproducing the results of simulate and filter, it is important to take these actions.
Set the same random number seed using
rng.Specify the same presample response data using the
Y0name-value argument.
Simulate 100 observations by passing the estimated model to simulate. Specify the entire data set as the presample.
rng("default")
YSim = simulate(EstMdl,100,Y0=Data);YSim is a 100-by-4 matrix of simulated responses. Columns correspond to the columns of the variables in EstMdl.SeriesNames.
Set the default random seed. Simulate 4 series of 100 observations from the standard Gaussian distribution.
rng("default")
Z = randn(100,4);Filter the Gaussian values through the estimated model. Specify the entire data set as the presample.
YFilter = filter(EstMdl,Z,Y0=Data);
YFilter is a 100-by-4 matrix of simulated responses. Columns correspond to the columns of the variables in EstMdl.SeriesNames. Before filtering the disturbances, filter scales Z by the lower triangular Cholesky factor of the model covariance in EstMdl.Covariance.
Compare the resulting responses between filter and simulate.
(YSim - YFilter)'*(YSim - YFilter)
ans = 4×4
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
The results are identical.
Consider this VEC(1) model for three hypothetical response series.
The innovations are multivariate Gaussian with a mean of 0 and the covariance matrix
Create variables for the parameter values.
A = [-0.3 0.3; -0.2 0.1; -1 0]; % Adjustment B = [0.1 -0.7; -0.2 0.5; 0.2 0.2]; % Cointegration Phi = {[0. 0.1 0.2; 0.2 -0.2 0; 0.7 -0.2 0.3]}; % ShortRun c = [-1; -3; -30]; % Constant tau = [0; 0; 0]; % Trend Sigma = [1.3 0.4 1.6; 0.4 0.6 0.7; 1.6 0.7 5]; % Covariance
Create a vecm model object representing the VEC(1) model using the appropriate name-value pair arguments.
Mdl = vecm(Adjustment=A,Cointegration=B, ...
Constant=c,ShortRun=Phi,Trend=tau,Covariance=Sigma);Mdl is effectively a fully specified vecm model object. That is, the cointegration constant and linear trend are unknown, but are not needed for simulating observations or forecasting given that the overall constant and trend parameters are known.
Simulate 1000 paths of 100 observations. Return the innovations (scaled disturbances).
rng(1); % For reproducibility
numpaths = 1000;
numobs = 100;
[Y,E] = simulate(Mdl,numobs,NumPaths=numpaths);Y is a 100-by-3-by-1000 matrix of simulated responses. E is a matrix whose dimensions correspond to the dimensions of Y, but represents the simulated, scaled disturbances. Columns correspond to the response variable names Mdl.SeriesNames.
For each time point, compute the mean vector of the simulated responses among all paths.
MeanSim = mean(Y,3);
MeanSim is a 100-by-7 matrix containing the average of the simulated responses at each time point.
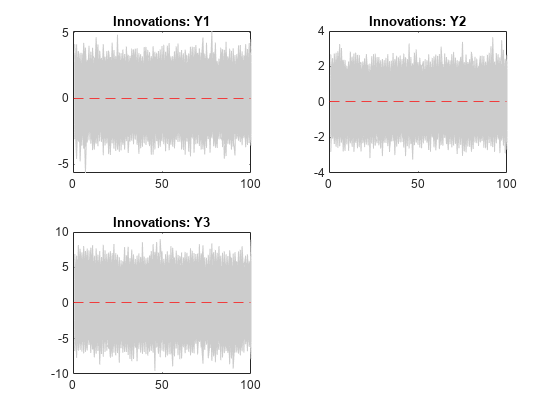
Plot the simulated responses and their averages, and plot the simulated innovations.
figure tiledlayout(2,2) for j = 1:numel(Mdl.SeriesNames) nexttile h1 = plot(squeeze(Y(:,j,:)),Color=[0.8 0.8 0.8]); hold on h2 = plot(MeanSim(:,j),Color="k",LineWidth=2); hold off title(Mdl.SeriesNames{j}); legend([h1(1) h2],["Simulated" "Mean"]) end
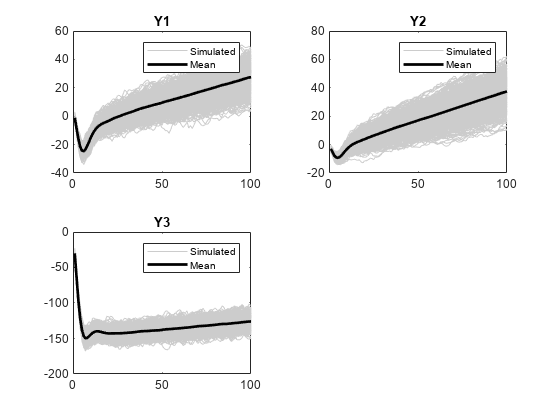
figure tiledlayout(2,2) for j = 1:numel(Mdl.SeriesNames) nexttile h1 = plot(squeeze(E(:,j,:)),Color=[0.8 0.8 0.8]); hold on yline(0,"r--") title("Innovations: " + Mdl.SeriesNames{j}) end
Since R2022b
Consider a VEC model for the following seven macroeconomic series, and then fit the model to a timetable of response data. This example is based on Return Response Series in Matrix from Unconditional Simulation.
Load and Preprocess Data
Load the Data_USEconVECModel data set.
load Data_USEconVECModel
DTT = FRED;
DTT.GDP = 100*log(DTT.GDP);
DTT.GDPDEF = 100*log(DTT.GDPDEF);
DTT.COE = 100*log(DTT.COE);
DTT.HOANBS = 100*log(DTT.HOANBS);
DTT.PCEC = 100*log(DTT.PCEC);
DTT.GPDI = 100*log(DTT.GPDI);Prepare Timetable for Estimation
When you plan to supply a timetable directly to estimate, you must ensure it has all the following characteristics:
All selected response variables are numeric and do not contain any missing values.
The timestamps in the
Timevariable are regular, and they are ascending or descending.
Remove all missing values from the table.
DTT = rmmissing(DTT); T = height(DTT)
T = 240
DTT does not contain any missing values.
Determine whether the sampling timestamps have a regular frequency and are sorted.
areTimestampsRegular = isregular(DTT,"quarters")areTimestampsRegular = logical
0
areTimestampsSorted = issorted(DTT.Time)
areTimestampsSorted = logical
1
areTimestampsRegular = 0 indicates that the timestamps of DTT are irregular. areTimestampsSorted = 1 indicates that the timestamps are sorted. Macroeconomic series in this example are timestamped at the end of the month. This quality induces an irregularly measured series.
Remedy the time irregularity by shifting all dates to the first day of the quarter.
dt = DTT.Time; dt = dateshift(dt,"start","quarter"); DTT.Time = dt;
DTT is regular with respect to time.
Create Model Template for Estimation
Create a VEC(1) model using the shorthand syntax. Specify the variable names.
Mdl = vecm(7,4,1); Mdl.SeriesNames = DTT.Properties.VariableNames;
Mdl is a vecm model object. All properties containing NaN values correspond to parameters to be estimated given data.
Fit Model to Data
Estimate the model by supplying the timetable of data DTT. By default, because the number of variables in Mdl.SeriesNames is the number of variables in DTT, estimate fits the model to all the variables in DTT.
EstMdl = estimate(Mdl,DTT); p = EstMdl.P
p = 2
EstMdl is an estimated vecm model object.
Perform Unconditional Simulation of Estimated Model
Simulate a response and innovations path from the estimated model and return the simulated series as variables in a timetable. simulate requires information for the output timetable, such as variable names, sampling times for the simulation horizon, and sampling frequency. Therefore, supply a presample of the earliest p = 2 observations of the data DTT, from which simulate infers the required timetable information. Specify a simulation horizon of numobs - p.
rng(1) % For reproducibility
PSTbl = DTT(1:p,:);
T = T - p;
Tbl = simulate(EstMdl,T,Presample=PSTbl);
size(Tbl)ans = 1×2
238 14
PSTbl
PSTbl=2×7 timetable
Time GDP GDPDEF COE HOANBS FEDFUNDS PCEC GPDI
___________ ______ ______ ______ ______ ________ ______ ______
01-Jan-1957 615.4 280.25 556.3 400.29 2.96 564.3 435.29
01-Apr-1957 615.87 280.95 557.03 400.07 3 565.11 435.54
head(Tbl)
Time GDP_Responses GDPDEF_Responses COE_Responses HOANBS_Responses FEDFUNDS_Responses PCEC_Responses GPDI_Responses GDP_Innovations GDPDEF_Innovations COE_Innovations HOANBS_Innovations FEDFUNDS_Innovations PCEC_Innovations GPDI_Innovations
___________ _____________ ________________ _____________ ________________ __________________ ______________ ______________ _______________ __________________ _______________ __________________ ____________________ ________________ ________________
01-Jul-1957 616.84 281.66 557.71 400.25 4.2485 566.28 434.68 -0.48121 0.20806 -0.61665 0.18593 0.76536 -0.27865 -1.4663
01-Oct-1957 619.27 282.31 559.72 400.14 4.0194 567.96 437.93 0.87578 0.087449 0.57148 -0.11607 -0.49734 0.41769 1.1751
01-Jan-1958 620.08 282.64 561.48 400.26 4.213 569.24 436.02 -0.56236 -0.12462 0.29936 0.13665 -0.36138 -0.16951 -2.7145
01-Apr-1958 620.73 282.94 562.02 400 4.2137 570.22 435.64 -0.82272 -0.074885 -0.56525 -0.36422 -0.15674 -0.25453 -2.5725
01-Jul-1958 621.25 283.36 562.07 400.21 4.2975 570.96 433.7 -0.62693 0.079973 -1.0419 0.33534 0.29843 -0.38226 -2.7238
01-Oct-1958 621.9 284.06 562.91 399.89 3.1839 571.64 431.99 -0.4246 0.3155 -0.2015 -0.080769 -0.99093 -0.27001 -2.4234
01-Jan-1959 622.57 284.44 564.48 399.68 4.0431 572.48 431.76 -0.41423 -0.093221 0.80092 0.30483 0.51348 -0.23757 -0.064299
01-Apr-1959 624.12 285 566.1 399.1 5.4039 574.44 432.44 0.13226 0.17348 0.88597 -0.46611 1.6584 0.88675 -1.7633
Tbl is a 238-by-14 matrix of simulated responses (denoted responseVariable_Responses) and corresponding innovations (denoted responseVariable_Innovations). The timestamps of Tbl follow directly from the timestamps of PSTbl, and they have the same sampling frequency.
Since R2022b
Consider the model and data in Return Response Series in Matrix from Unconditional Simulation.
Load the Data_USEconVECModel data set.
load Data_USEconVECModelThe Data_Recessions data set contains the beginning and ending serial dates of recessions. Load this data set. Convert the matrix of date serial numbers to a datetime array.
load Data_Recessions dtrec = datetime(Recessions,ConvertFrom="datenum");
Remove the exponential trend from the series, and then scale them by a factor of 100.
DTT = FRED; DTT.GDP = 100*log(DTT.GDP); DTT.GDPDEF = 100*log(DTT.GDPDEF); DTT.COE = 100*log(DTT.COE); DTT.HOANBS = 100*log(DTT.HOANBS); DTT.PCEC = 100*log(DTT.PCEC); DTT.GPDI = 100*log(DTT.GPDI);
Create a dummy variable that identifies periods in which the U.S. was in a recession or worse. Specifically, the variable should be 1 if FRED.Time occurs during a recession, and 0 otherwise. Include the variable with the FRED data.
isin = @(x)(any(dtrec(:,1) <= x & x <= dtrec(:,2))); DTT.IsRecession = double(arrayfun(isin,DTT.Time));
Remove all missing values from the table.
DTT = rmmissing(DTT);
To make the series regular, shift all dates to the first day of the quarter.
dt = DTT.Time; dt = dateshift(dt,"start","quarter"); DTT.Time = dt;
DTT is regular with respect to time.
Create separate presample and estimation sample data sets. The presample contains the earliest p = 2 observations, and the estimation sample contains the rest of the data.
p = 2;
PSTbl = DTT(1:p,:);
InSample = DTT((p+1):end,:);
prednames = "IsRecession";Create a VEC(1) model using the shorthand syntax. Assume that the appropriate cointegration rank is 4. You do not have to specify the presence of a regression component when creating the model. Specify the variable names.
Mdl = vecm(7,4,p-1); Mdl.SeriesNames = DTT.Properties.VariableNames(1:end-1);
Estimate the model using the entire in-sample data InSample, and specify the presample PSTbl. Specify the predictor identifying whether the observation was measured during a recession.
EstMdl = estimate(Mdl,InSample,PredictorVariables="IsRecession", ... Presample=PSTbl);
Generate 100 random response and innovations paths from the estimated model by performing an unconditional simulation. Specify that the length of the paths is the same as the length of the estimation sample period. Supply the presample and estimation sample data, and specify the predictor variable name.
rng(1) % For reproducibility numpaths = 100; numobs = height(InSample); Tbl = simulate(EstMdl,numobs,NumPaths=numpaths, ... Presample=PSTbl,InSample=InSample,PredictorVariables=prednames); size(Tbl)
ans = 1×2
238 22
head(Tbl(:,endsWith(Tbl.Properties.VariableNames,["_Responses" "Innovations"])))
Time GDP_Responses GDPDEF_Responses COE_Responses HOANBS_Responses FEDFUNDS_Responses PCEC_Responses GPDI_Responses GDP_Innovations GDPDEF_Innovations COE_Innovations HOANBS_Innovations FEDFUNDS_Innovations PCEC_Innovations GPDI_Innovations
___________ _____________ ________________ _____________ ________________ __________________ ______________ ______________ _______________ __________________ _______________ __________________ ____________________ ________________ ________________
01-Jul-1957 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double
01-Oct-1957 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double
01-Jan-1958 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double
01-Apr-1958 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double
01-Jul-1958 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double
01-Oct-1958 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double
01-Jan-1959 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double
01-Apr-1959 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double
Tbl is a 238-by-22 timetable of estimation sample data, simulated responses (denoted responseName_Responses) and corresponding innovations (denoted responseName_Innovations). The simulated response and innovations variables are 238-by-100 matrices, where wach row is a period in the estimation sample and each column is a separate, independently generated path.
For each time in the estimation sample, compute the mean vector of the simulated responses among all paths.
idx = endsWith(Tbl.Properties.VariableNames,"_Responses");
simrespnames = Tbl.Properties.VariableNames(idx);
MeanSim = varfun(@(x)mean(x,2),Tbl,InputVariables=simrespnames);MeanSim is a 238-by-7 timetable containing the average of the simulated responses at each time point.
Plot the simulated responses, their averages, and the data.
figure tiledlayout(2,2) for j = 1:4 nexttile plot(Tbl.Time,Tbl{:,simrespnames(j)},Color=[0.8,0.8,0.8]) title(Mdl.SeriesNames{j}); hold on h1 = plot(Tbl.Time,Tbl{:,Mdl.SeriesNames(j)}); h2 = plot(Tbl.Time,MeanSim{:,"Fun_"+simrespnames(j)}); hold off end
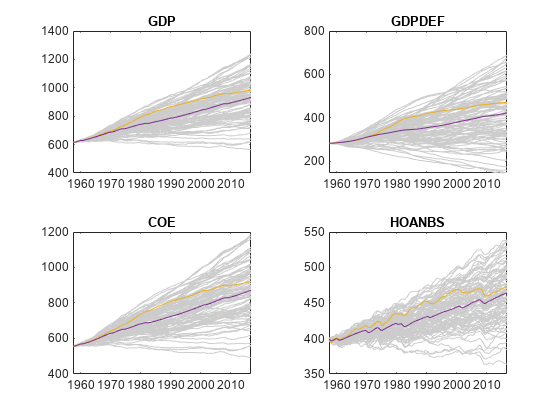
figure tiledlayout(2,2) for j = 5:7 nexttile plot(Tbl.Time,Tbl{:,simrespnames(j)},Color=[0.8,0.8,0.8]) title(Mdl.SeriesNames{j}); hold on h1 = plot(Tbl.Time,Tbl{:,Mdl.SeriesNames(j)}); h2 = plot(Tbl.Time,MeanSim{:,"Fun_"+simrespnames(j)}); hold off end

Since R2022b
Perform a conditional simulation of the VEC model in Return Response Series in Matrix from Unconditional Simulation, in which economists hypothesize that the effective federal funds rate is 0.5% for 12 quarters after the end of the sampling period (from Q1 of 2017 through Q4 of 2019).
Load and Preprocess Data
Load the Data_USEconVECModel data set.
load Data_USEconVECModel
DTT = FRED;
DTT.GDP = 100*log(DTT.GDP);
DTT.GDPDEF = 100*log(DTT.GDPDEF);
DTT.COE = 100*log(DTT.COE);
DTT.HOANBS = 100*log(DTT.HOANBS);
DTT.PCEC = 100*log(DTT.PCEC);
DTT.GPDI = 100*log(DTT.GPDI);Prepare Timetable for Estimation
Remove all missing values from the table.
DTT = rmmissing(DTT);
To make the series regular, shift all dates to the first day of the quarter.
dt = DTT.Time; dt = dateshift(dt,"start","quarter"); DTT.Time = dt;
DTT is regular with respect to time.
Create Model Template for Estimation
Create a VEC(1) model using the shorthand syntax. Specify the variable names.
Mdl = vecm(7,4,1); Mdl.SeriesNames = DTT.Properties.VariableNames;
Mdl is a vecm model object. All properties containing NaN values correspond to parameters to be estimated given data.
Fit Model to Data
Estimate the model. Pass the entire timetable DTT. Because the VEC model is 7-D and the estimation data contains seven variables, estimate selects all response variables in the data by default. Alternatively, you can use the ResponseVariables name-value argument.
EstMdl = estimate(Mdl,DTT);
Prepare for Conditional Simulation of Estimated Model
Suppose economists hypothesize that the effective federal funds rate will be at 0.5% for the next 12 quarters.
Create a timetable with the following qualities:
The timestamps are regular with respect to the estimation sample timestamps and they are ordered from Q1 of 2017 through Q4 of 2019.
All variables of DTT, except for
FEDFUNDS, are a 12-by-1 vector ofNaNvalues.FEDFUNDSis a 12-by-1 vector, where each element is 0.5.
numobs = 12;
shdt = DTT.Time(end) + calquarters(1:numobs);
DTTCondSim = retime(DTT,shdt,"fillwithmissing");
DTTCondSim.FEDFUNDS = 0.5*ones(numobs,1);DTTCondSim is a 12-by-7 timetable that follows directly, in time, from DTT, and both timetables have the same variables. All variables in DTTCondSim contain NaN values, except for FEDFUNDS, which is a vector composed of the value 0.5.
Perform Conditional Simulation of Estimated Model
Simulate all variables given the hypothesis by supplying the conditioning data DTTCondSim and specifying the response variable names. Generate 100 paths. Because the simulation horizon is beyond the estimation sample data, supply the estimation sample as a presample to initialize the model.
rng(1) % For reproducibility Tbl = simulate(EstMdl,numobs,NumPaths=100, ... InSample=DTTCondSim,ResponseVariables=EstMdl.SeriesNames, ... Presample=DTT,PresampleResponseVariables=EstMdl.SeriesNames); size(Tbl)
ans = 1×2
12 21
idx = endsWith(Tbl.Properties.VariableNames,["_Responses" "_Innovations"]); head(Tbl(:,idx))
Time GDP_Responses GDPDEF_Responses COE_Responses HOANBS_Responses FEDFUNDS_Responses PCEC_Responses GPDI_Responses GDP_Innovations GDPDEF_Innovations COE_Innovations HOANBS_Innovations FEDFUNDS_Innovations PCEC_Innovations GPDI_Innovations
___________ _____________ ________________ _____________ ________________ __________________ ______________ ______________ _______________ __________________ _______________ __________________ ____________________ ________________ ________________
01-Jan-2017 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double
01-Apr-2017 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double
01-Jul-2017 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double
01-Oct-2017 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double
01-Jan-2018 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double
01-Apr-2018 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double
01-Jul-2018 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double
01-Oct-2018 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double 1×100 double
Tbl is a 12-by-21 matrix of simulated responses and innovations of all variables in the simulation horizon, given FEDFUNDS is 0.5%. GDP_Responses contains the simulated paths of the transformed GDP and GDP_Innovations contains the corresponding innovations series. FEDFUNDS_Responses is a 12-by-100 matrix composed of the value 0.5.
Plot the simulated values of the variables and their period-wise means.
idx = (endsWith(Tbl.Properties.VariableNames,"_Responses") + ... ~startsWith(Tbl.Properties.VariableNames,"FEDFUNDS")) == 2; simrespnames = Tbl.Properties.VariableNames(idx); MeanSim = varfun(@(x)mean(x,2),Tbl,InputVariables=simrespnames); figure tiledlayout(3,2) for j = simrespnames nexttile h1 = plot(Tbl.Time,Tbl{:,j},Color=[0.8,0.8,0.8]); title(erase(j,"_Responses")); hold on h2 = plot(Tbl.Time,MeanSim{:,"Fun_"+j}); hold off end hl = legend([h1(1) h2],"Simulation","Simulation Mean", ... Location="northwest");

Input Arguments
Since R2022b
Presample data that provides initial values for the model Mdl,
specified as a table or timetable with numprevars variables and
numpreobs rows. The following situations describe when to use
Presample:
Presampleis required whensimulateperforms an unconditional simulation, which occurs under one of the following conditions:You do not supply data in the simulation horizon (that is, you do not use the
InSamplename-value argument).You specify only predictor data for the model regression component in the simulation horizon using the
InSampleandPredictorVariablesname-value arguments, but you do not select any response variables fromInSample.
Presampleis optional whensimulateperforms a conditional simulation, that is, when you supply response data in the simulation horizon, on which to condition the simulated responses, by using theInSampleandResponseVariablesname-value arguments. By default,simulatesets any necessary presample observations.For stationary VAR processes without regression components,
simulatesets presample observations to the unconditional meanFor nonstationary processes or models that contain a regression component,
simulatesets presample observations to zero.
Regardless of the situation, simulate returns the
simulated variables in the output table or timetable Tbl, which is
commensurate with Presample.
Each row is a presample observation, and measurements in each row, among all paths,
occur simultaneously. numpreobs must be at least
Mdl.P. If you supply more rows than necessary,
simulate uses the latest Mdl.P
observations only.
Each variable is a numpreobs-by-numprepaths
numeric matrix. Variables are associated with response series in
Mdl.SeriesNames. To control presample variable selection, see the
optional PresampleResponseVariables name-value argument.
For each variable, columns are separate, independent paths.
If variables are vectors,
simulateapplies them to each respective path to initialize the model for the simulation. Therefore, all respective response paths derive from common initial conditions.Otherwise, for each variable
ResponseKjsimulateappliesPresample.to produceResponseK(:,j)Tbl.ResponseK(:,. Variables must have at leastj)numpathscolumns, andsimulateuses only the firstnumpathscolumns.
If Presample is a timetable, all the following conditions must be true:
Presamplemust represent a sample with a regular datetime time step (seeisregular).The inputs
InSampleandPresamplemust be consistent in time such thatPresampleimmediately precedesInSamplewith respect to the sampling frequency and order.The datetime vector of sample timestamps
Presample.Timemust be ascending or descending.
If Presample is a table, the last row contains the latest
presample observation.
Since R2022b
Future time series response or predictor data, specified as a table or timetable.
InSample contains numvars variables, including
numseries response variables
yt or numpreds predictor
variables xt for the model regression component.
You can specify InSample only when other data inputs are tables or
timetables.
Use InSample in the following situations:
Perform conditional simulation. You must also supply the response variable names in
InSampleby using theResponseVariablesname-value argument.Supply future predictor data for either unconditional or conditional simulation. To supply predictor data, you must specify predictor variable names in
InSampleby using thePredictorVariablesname-value argument. Otherwise,simulateignores the model regression component.
simulate returns the simulated variables in the
output table or timetable Tbl, which is commensurate with
InSample.
Each row corresponds to an observation in the simulation horizon, the first row is the earliest observation, and measurements in each row, among all paths, occur simultaneously. InSample must have at least numobs rows to cover the simulation horizon. If you supply more rows than necessary, simulate uses only the first numobs rows.
Each response variable is a numeric matrix with numpaths columns. For each
response variable KjResponseKResponseKPresample.) into the future.
For each selected response variable ResponseKResponseK
If
InSample.is a vector,ResponseKsimulateapplies to each of thenumpathsoutput paths (seeNumPaths).Otherwise,
InSample.must have at leastResponseKnumpathscolumns. If you supply more pages than necessary,simulateuses only the firstnumpathscolumns.
Each predictor variable is a numeric vector. All predictor variables are present in the regression component of each response equation and apply to all response paths.
If InSample is a timetable, the following conditions apply:
If InSample is a table, the last row contains the latest
observation.
Elements of the response variables of InSample can be numeric scalars or missing values (indicated by NaN values). simulate treats numeric scalars as deterministic future responses that are known in advance, for example, set by policy. simulate simulates responses for corresponding NaN values conditional on the known values. Elements of selected predictor variables must be numeric scalars.
By default, simulate performs an unconditional simulation without a
regression component in the model (each selected response variable is a
numobs-by-numpaths matrix composed of
NaN values indicating a complete lack of knowledge of the future
state of all simulated responses). Therefore, variables in Tbl result
from a conventional, unconditional Monte Carlo simulation.
For more details, see Algorithms.
Example: Consider simulating one path from a model composed of two response
series, GDP and CPI, three periods
into the future. Suppose that you have prior knowledge about some of the
future values of the responses, and you want to simulate the unknown
responses conditional on your knowledge. Specify InSample
as a table containing the values that you know, and use
NaN for values you do not know but want to simulate.
For example, InSample=array2table([2 NaN; 0.1 NaN; NaN
NaN],VariableNames=["GDP" "CPI"]) specifies that you have no
knowledge of the future values of CPI, but you know that
GDP is 2, 0.1, and unknown in periods 1, 2, and 3,
respectively, in the simulation horizon.
Since R2022b
Variables to select from InSample to treat as response variables
yt, specified as one of the following
data types:
String vector or cell vector of character vectors containing
numseriesvariable names inInSample.Properties.VariableNamesA length
numseriesvector of unique indices (integers) of variables to select fromInSample.Properties.VariableNamesA length
numvarslogical vector, whereResponseVariables(selects variablej) = truejInSample.Properties.VariableNames, andsum(ResponseVariables)isnumseries
To perform conditional simulation, you must specify
ResponseVariables to select the response variables in
InSample for the conditioning data.
ResponseVariables applies only when you specify
InSample.
The selected variables must be numeric vectors (single path) or matrices (columns represent multiple independent paths) of the same width.
Example: ResponseVariables=["GDP" "CPI"]
Example: ResponseVariables=[true false true false] or
ResponseVariable=[1 3] selects the first and third table
variables as the response variables.
Data Types: double | logical | char | cell | string
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: simulate(Mdl,100,Presample=PSTbl,PresampleResponseVariables=["GDP"
"CPI"]) returns a timetable of variables containing 100-period
simulated response and innovations series from Mdl, initialized
by the data in the GDP and CPI variables of
the timetable of presample data in PSTbl..
Presample responses that provide initial values for the model
Mdl, specified as a
numpreobs-by-numseries numeric matrix or a
numpreobs-by-numseries-by-numprepaths
numeric array. Use Y0 only when you supply optional data inputs as
numeric arrays.
numpreobs is the number of presample observations.
numprepaths is the number of presample response paths.
Each row is a presample observation, and measurements in each row, among all pages,
occur simultaneously. The last row contains the latest presample observation.
Y0 must have at least Mdl.P rows. If you
supply more rows than necessary, simulate uses the latest
Mdl.P observations only.
Each column corresponds to the response series name in
Mdl.SeriesNames.
Pages correspond to separate, independent paths.
If
Y0is a matrix,simulateapplies it to simulate each sample path (page). Therefore, all paths in the output argumentYderive from common initial conditions.Otherwise,
simulateappliesY0(:,:,to initialize simulating pathj)j.Y0must have at leastnumpathspages, andsimulateuses only the firstnumpathspages.
By default, simulate sets any necessary presample observations.
For stationary VAR processes without regression components,
simulatesets presample observations to the unconditional meanFor nonstationary processes or models that contain a regression component,
simulatesets presample observations to zero.
Data Types: double
Since R2022b
Variables to select from Presample to use for presample data, specified
as one of the following data types:
String vector or cell vector of character vectors containing
numseriesvariable names inPresample.Properties.VariableNamesA length
numseriesvector of unique indices (integers) of variables to select fromPresample.Properties.VariableNamesA length
numprevarslogical vector, wherePresampleResponseVariables(selects variablej) = truejPresample.Properties.VariableNames, andsum(PresampleResponseVariables)isnumseries
PresampleResponseVariables applies only when you specify
Presample.
The selected variables must be numeric vectors and cannot contain missing values
(NaN).
PresampleResponseNames does not need to contain the same names as in
Mdl.SeriesNames; simulate uses the data in
selected variable PresampleResponseVariables(
as a presample for j)Mdl.SeriesNames(.j)
If the number of variables in Presample matches
Mdl.NumSeries, the default specifies all variables in
Presample. If the number of variables in Presample
exceeds Mdl.NumSeries, the default matches variables in
Presample to names in Mdl.SeriesNames.
Example: PresampleResponseVariables=["GDP" "CPI"]
Example: PresampleResponseVariables=[true false true false] or
PresampleResponseVariable=[1 3] selects the first and third table
variables for presample data.
Data Types: double | logical | char | cell | string
Predictor data for the regression component in the model, specified as a numeric
matrix containing numpreds columns. Use X only
when you supply optional data inputs as numeric arrays.
numpreds is the number of predictor variables
(size(Mdl.Beta,2)).
Each row corresponds to an observation, and measurements in each row occur
simultaneously. The last row contains the latest observation. X must
have at least numobs rows. If you supply more rows than necessary,
simulate uses only the latest numobs
observations. simulate does not use the regression component in
the presample period.
Each column is an individual predictor variable. All predictor variables are present in the regression component of each response equation.
simulate applies X to each path (page);
that is, X represents one path of observed predictors.
By default, simulate excludes the regression component,
regardless of its presence in Mdl.
Data Types: double
Since R2022b
Variables to select from InSample to treat as exogenous predictor
variables xt, specified as one of the following data types:
String vector or cell vector of character vectors containing
numpredsvariable names inInSample.Properties.VariableNamesA length
numpredsvector of unique indices (integers) of variables to select fromInSample.Properties.VariableNamesA length
numvarslogical vector, wherePredictorVariables(selects variablej) = truejInSample.Properties.VariableNames, andsum(PredictorVariables)isnumpreds
Regardless, selected predictor variable
jMdl.Beta(:,.j)
PredictorVariables applies only when you specify
InSample.
The selected variables must be numeric vectors and cannot contain missing values
(NaN).
By default, simulate excludes the regression component, regardless
of its presence in Mdl.
Example: PredictorVariables=["M1SL" "TB3MS" "UNRATE"]
Example: PredictorVariables=[true false true false] or
PredictorVariable=[1 3] selects the first and third table variables as
the response variables.
Data Types: double | logical | char | cell | string
Future multivariate response series for conditional simulation, specified as a numeric matrix
or array containing numseries columns. Use YF only
when you supply optional data inputs as numeric arrays.
Each row corresponds to observations in the simulation horizon, and the first row is the
earliest observation. Specifically, row j in sample path
k
(YF()
contains the responses j,:,k)j periods into the future.
YF must have at least numobs rows to cover the
simulation horizon. If you supply more rows than necessary, simulate
uses only the first numobs rows.
Each column corresponds to the response variable name in
Mdl.SeriesNames.
Each page corresponds to a separate sample path. Specifically, path
k (YF(:,:,)
captures the state, or knowledge, of the response series as they evolve from the presample
past (k)Y0) into the future.
If
YFis a matrix,simulateappliesYFto each of thenumpathsoutput paths (seeNumPaths).Otherwise,
YFmust have at leastnumpathspages. If you supply more pages than necessary,simulateuses only the firstnumpathspages.
Elements of YF can be numeric scalars or missing values (indicated by
NaN values). simulate treats numeric scalars
as deterministic future responses that are known in advance, for example, set by policy.
simulate simulates responses for corresponding
NaN values conditional on the known values.
By default, YF is an array composed of NaN values indicating a complete lack of knowledge of the future state of all simulated responses. Therefore, simulate obtains the output responses Y from a conventional, unconditional Monte Carlo simulation.
For more details, see Algorithms.
Example: Consider simulating one path from a model composed of four
response series three periods into the future. Suppose that you have
prior knowledge about some of the future values of the responses, and
you want to simulate the unknown responses conditional on your
knowledge. Specify YF as a matrix containing the
values that you know, and use NaN for values you do
not know but want to simulate. For example, 'YF',[NaN 2 5 NaN;
NaN NaN 0.1 NaN; NaN NaN NaN NaN] specifies that you have
no knowledge of the future values of the first and fourth response
series; you know the value for period 1 in the second response series,
but no other value; and you know the values for periods 1 and 2 in the
third response series, but not the value for period 3.
Data Types: double
Note
NaNvalues inY0andXindicate missing values.simulateremoves missing values from the data by list-wise deletion. IfY0is a 3-D array, thensimulateperforms these steps:Horizontally concatenate pages to form a
numpreobs-by-numpaths*numseriesmatrix.Remove any row that contains at least one
NaNfrom the concatenated data.
In the case of missing observations, the results obtained from multiple paths of
Y0can differ from the results obtained from each path individually.For conditional simulation (see
YF), ifXcontains any missing values in the latestnumobsobservations, thensimulateissues an error.simulateissues an error when selected response variables fromPresampleand selected predictor variables fromInSamplecontain any missing values.
Output Arguments
Simulated multivariate response series, returned as a
numobs-by-numseries numeric matrix or a
numobs-by-numseries-by-numpaths
numeric array. simulate returns Y only when
you supply optional data sets as numeric matrices or arrays, for example, you use the
Y0 name-value argument.
Y represents the continuation of the presample responses in
Y0.
Each row is a time point in the simulation horizon. Values in a row, among all pages, occur simultaneously. The last row contains the latest simulated values.
Each column corresponds to the response series name in
Mdl.SeriesNames.
Pages correspond to separate, independently simulated paths.
If you specify future responses for conditional simulation using the
YF name-value argument, the known values in
YF appear in the same positions in Y. However,
Y contains simulated values for the missing observations in
YF.
Simulated multivariate model innovations series, returned as a
numobs-by-numseries numeric matrix or a
numobs-by-numseries-by-numpaths
numeric array. simulate returns E only when
you supply optional data sets as numeric matrices or arrays, for example, you use the
Y0 name-value argument.
Elements of E and Y correspond.
If you specify future responses for conditional simulation (see the
YF name-value argument), simulate
infers the innovations from the known values in YF and places the
inferred innovations in the corresponding positions in E. For the
missing observations in YF, simulate draws
from the Gaussian distribution conditional on any known values, and places the draws in
the corresponding positions in E.
Since R2022b
Simulated multivariate response, model innovations, and other variables, returned as a
table or timetable, the same data type as Presample or
InSample. simulate returns
Tbl only when you supply at least one of the inputs
Presample and InSample.
Tbl contains the following variables:
The simulated paths within the simulation horizon of the selected response series yt. Each simulated response variable in
Tblis anumobs-by-numpathsnumeric matrix, wherenumobsis the value ofNumObsandnumpathsis the value ofNumPaths. Each row corresponds to a time in the simulation horizon and each column corresponds to a separate path.simulatenames the simulated response variableResponseKResponseK_ResponsesMdl.Series(isK)GDP,Tblcontains a variable for the corresponding simulated response with the nameGDP_Responses. If you specifyResponseVariables,ResponseKResponseVariable(. Otherwise,K)ResponseKPresampleResponseVariable(.K)The simulated paths within the simulation horizon of the innovations εt corresponding to yt. Each simulated innovations variable in
Tblis anumobs-by-numpathsnumeric matrix. Each row corresponds to a time in the simulation horizon and each column corresponds to a separate path.simulatenames the simulated innovations variable of responseResponseKResponseK_InnovationsMdl.Series(isK)GDP,Tblcontains a variable for the corresponding innovations with the nameGDP_Innovations.
If Tbl is a timetable, the following conditions hold:
The row order of
Tbl, either ascending or descending, matches the row order ofInSample, when you specify it. If you do not specifyInSampleand you specifyPresample, the row order ofTblis the same as the row orderPresample.If you specify
InSample, row timesTbl.TimeareInSample.Time(1:numobs). Otherwise,Tbl.Time(1)is the next time afterPresample(end)relative to the sampling frequency, andTbl.Time(2:numobs)are the following times relative to the sampling frequency.
Algorithms
simulateperforms conditional simulation using this process for all pagesk= 1,...,numpathsand for each timet= 1,...,numobs.simulateinfers (or inverse filters) the model innovations for all response variables (E(from the known future responses (t,:,k)YF(). Int,:,k)E,simulatemimics the pattern ofNaNvalues that appears inYF.For the missing elements of
Eat timet,simulateperforms these steps.Draw
Z1, the random, standard Gaussian distribution disturbances conditional on the known elements ofE.Scale
Z1by the lower triangular Cholesky factor of the conditional covariance matrix. That is,Z2=L*Z1, whereL=chol(C,"lower")andCis the covariance of the conditional Gaussian distribution.Impute
Z2in place of the corresponding missing values inE.
For the missing values in
YF,simulatefilters the corresponding random innovations through the modelMdl.
simulateuses this process to determine the time origin t0 of models that include linear time trends.If you do not specify
Y0, then t0 = 0.Otherwise,
simulatesets t0 tosize(Y0,1)–Mdl.P. Therefore, the times in the trend component are t = t0 + 1, t0 + 2,..., t0 +numobs. This convention is consistent with the default behavior of model estimation in whichestimateremoves the firstMdl.Presponses, reducing the effective sample size. Althoughsimulateexplicitly uses the firstMdl.Ppresample responses inY0to initialize the model, the total number of observations inY0(excluding any missing values) determines t0.
References
[1] Hamilton, James D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.
[2] Johansen, S. Likelihood-Based Inference in Cointegrated Vector Autoregressive Models. Oxford: Oxford University Press, 1995.
[3] Juselius, K. The Cointegrated VAR Model. Oxford: Oxford University Press, 2006.
[4] Lütkepohl, H. New Introduction to Multiple Time Series Analysis. Berlin: Springer, 2005.
Version History
Introduced in R2017bIn addition to accepting input data in numeric arrays,
simulate accepts input data in tables and timetables. simulate chooses default series on which to operate, but you can use the following name-value arguments to select variables.
Presamplespecifies the input table or regular timetable of presample response data.PresampleResponseVariablesspecifies the response series names inPresample.Insamplespecifies the table or regular timetable of future response and predictor data for conditional simulation.ResponseVariablesspecifies the response series names inInSample.PredictorVariablesspecifies the predictor series inInSamplefor a model regression component.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Web サイトの選択
Web サイトを選択すると、翻訳されたコンテンツにアクセスし、地域のイベントやサービスを確認できます。現在の位置情報に基づき、次のサイトの選択を推奨します:
また、以下のリストから Web サイトを選択することもできます。
最適なサイトパフォーマンスの取得方法
中国のサイト (中国語または英語) を選択することで、最適なサイトパフォーマンスが得られます。その他の国の MathWorks のサイトは、お客様の地域からのアクセスが最適化されていません。
南北アメリカ
- América Latina (Español)
- Canada (English)
- United States (English)
ヨーロッパ
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)