mixconjugateblm

Bayesian linear regression model with conjugate priors for stochastic search variable selection (SSVS)

Description

The Bayesian linear regression model object mixconjugateblm specifies the joint prior distribution of the regression coefficients and the disturbance variance (β, σ²) for implementing SSVS (see [1] and [2]) assuming β and σ² are dependent random variables.

In general, when you create a Bayesian linear regression model object, it specifies the joint prior distribution and characteristics of the linear regression model only. That is, the model object is a template intended for further use. Specifically, to incorporate data into the model for posterior distribution analysis and feature selection, pass the model object and data to the appropriate object function.

Creation

Syntax

PriorMdl = mixconjugateblm(NumPredictors)

PriorMdl = mixconjugateblm(NumPredictors,Name,Value)

Description

PriorMdl = mixconjugateblm(NumPredictors) creates a Bayesian linear regression model object (PriorMdl) composed of NumPredictors predictors and an intercept, and sets the NumPredictors property. The joint prior distribution of (β, σ²) is appropriate for implementing SSVS for predictor selection [2]. PriorMdl is a template that defines the prior distributions and the dimensionality of β.

PriorMdl = mixconjugateblm(NumPredictors,Name,Value) sets properties (except NumPredictors) using name-value pair arguments. Enclose each property name in quotes. For example, mixconjugateblm(3,'Probability',abs(rand(4,1))) specifies random prior regime probabilities for all four coefficients in the model.

Properties

You can set writable property values when you create the model object by using name-value argument syntax, or after you create the model object by using dot notation. For example, to exclude an intercept from the model, enter

PriorMdl.Intercept = false;

NumPredictors — Number of predictor variables

nonnegative integer

Number of predictor variables in the Bayesian multiple linear regression model, specified as a nonnegative integer.

NumPredictors must be the same as the number of columns in your predictor data, which you specify during model estimation or simulation.

When specifying NumPredictors, exclude any intercept term for the value.

After creating a model, if you change the of value NumPredictors using dot notation, then these parameters revert to the default values:

• Variables names (VarNames)

• Prior mean of β (Mu)

• Prior variances of β for each regime (V)

• Prior correlation matrix of β (Correlation)

• Prior regime probabilities (Probability)

Data Types: double

Intercept — Flag for including regression model intercept

true (default) | false

Flag for including a regression model intercept, specified as a value in this table.

Value	Description
false	Exclude an intercept from the regression model. Therefore, β is a p-dimensional vector, where p is the value of NumPredictors.
true	Include an intercept in the regression model. Therefore, β is a (p + 1)-dimensional vector. This specification causes a T-by-1 vector of ones to be prepended to the predictor data during estimation and simulation.

If you include a column of ones in the predictor data for an intercept term, then set Intercept to false.

Example: 'Intercept',false

Data Types: logical

VarNames — Predictor variable names

string vector | cell vector of character vectors

Predictor variable names for displays, specified as a string vector or cell vector of character vectors. VarNames must contain NumPredictors elements. VarNames(j) is the name of the variable in column j of the predictor data set, which you specify during estimation, simulation, or forecasting.

The default is {'Beta(1)','Beta(2),...,Beta(p)}, where p is the value of NumPredictors.

Example: 'VarNames',["UnemploymentRate"; "CPI"]

Data Types: string | cell | char

Mu — Component-wise mean hyperparameter of Gaussian mixture prior on β

zeros(Intercept + NumPredictors,2) (default) | numeric matrix

Component-wise mean hyperparameter of the Gaussian mixture prior on β, specified as an (Intercept + NumPredictors)-by-2 numeric matrix. The first column contains the prior means for component 1 (the variable-inclusion regime, that is, γ = 1). The second column contains the prior means for component 2 (the variable-exclusion regime, that is, γ = 0).

• If Intercept is false, then Mu has NumPredictors rows. mixconjugateblm sets the prior mean of the NumPredictors coefficients corresponding to the columns in the predictor data set, which you specify during estimation, simulation, or forecasting.

• Otherwise, Mu has NumPredictors + 1 elements. The first element corresponds to the prior means of the intercept, and all other elements correspond to the predictor variables.

Tip

To perform SSVS, use the default value of Mu.

Example: In a 3-coefficient model, 'Mu',[0.5 0; 0.5 0; 0.5 0] sets the component 1 prior mean of all coefficients to 0.5 and sets the component 2 prior mean of all coefficients to 0.

Data Types: double

V — Component-wise variance factor hyperparameter of Gaussian mixture prior on β

repmat([10 0.1],Intercept + NumPredictors,1) (default) | positive numeric matrix

Component-wise variance factor hyperparameter of the Gaussian mixture prior on β, an (Intercept + NumPredictors)-by-2 positive numeric matrix. The first column contains the prior variance factors for component 1 (the variable-inclusion regime, that is, γ = 1). The second column contains the prior variance factors for component 2 (the variable-exclusion regime, that is, γ = 0). Regardless of regime or coefficient, the prior variance of a coefficient is the variance factor times σ².

• If Intercept is false, then V has NumPredictors rows. mixconjugateblm sets the prior variance factor of the NumPredictors coefficients corresponding to the columns in the predictor data set, which you specify during estimation, simulation, or forecasting.

• Otherwise, V has NumPredictors + 1 elements. The first element corresponds to the prior variance factor of the intercept, and all other elements correspond to the predictor variables.

Tip

• To perform SSVS, specify a larger variance factor for regime 1 than for regime 2 (for all j, specify V(j,1) > V(j,2)).

• For more details on what value to specify for V, see [1].

Example: In a 3-coefficient model, 'V',[100 1; 100 1; 100 1] sets the component 1 prior variance factor of all coefficients to 100 and sets the component 2 prior variance factor of all coefficients to 1.

Data Types: double

Probability — Prior probability distribution for variable inclusion and exclusion regimes

0.5*ones(Intercept + NumPredictors,1) (default) | numeric vector of values in [0,1] | function handle

Prior probability distribution for the variable inclusion and exclusion regimes, specified as an (Intercept + NumPredictors)-by-1 numeric vector of values in [0,1], or a function handle in the form @fcnName, where fcnName is the function name. Probability represents the prior probability distribution of γ = {γ₁,…,γ_K}, where:

• K = Intercept + NumPredictors, which is the number of coefficients in the regression model.

• γ_k ∈ {0,1} for k = 1,…,K. Therefore, the sample space has a cardinality of 2^K.

• γ_k = 1 indicates variable VarNames(k) is included in the model, and γ_k = 0 indicates that the variable is excluded from the model.

If Probability is a numeric vector:

• Rows correspond to the variable names in VarNames. For models containing an intercept, the prior probability for intercept inclusion is Probability(1).

• For k = 1,…,K, the prior probability for excluding variable k is 1 – Probability(k).

• Prior probabilities of the variable-inclusion regime, among all variables and the intercept, are independent.

If Probability is a function handle, then it represents a custom prior distribution of the variable-inclusion regime probabilities. The corresponding function must have this declaration statement (the argument and function names can vary):

logprob = regimeprior(varinc)

• logprob is a numeric scalar representing the log of the prior distribution. You can write the prior distribution up to a proportionality constant.

• varinc is a K-by-1 logical vector. Elements correspond to the variable names in VarNames and indicate the regime in which the corresponding variable exists. varinc(k) = true indicates VarName(k) is included in the model, and varinc(k) = false indicates it is excluded from the model.

You can include more input arguments, but they must be known when you call mixconjugateblm.

For details on what value to specify for Probability, see [1].

Example: In a 3-coefficient model, 'Probability',rand(3,1) assigns random prior variable-inclusion probabilities to each coefficient.

Data Types: double | function_handle

Correlation — Prior correlation matrix of β

eye(Intercept + NumPredictors) (default) | numeric, positive definite matrix

Prior correlation matrix of β for both components in the mixture model, specified as an (Intercept + NumPredictors)-by-(Intercept + NumPredictors) numeric, positive definite matrix. Consequently, the prior covariance matrix for component j in the mixture model is sigma2*diag(sqrt(V(:,j)))*Correlation*diag(sqrt(V(:,j))), where sigma2 is σ² and V is the matrix of coefficient variance factors.

Rows and columns correspond to the variable names in VarNames.

By default, regression coefficients are uncorrelated, conditional on the regime.

Note

You can supply any appropriately sized numeric matrix. However, if your specification is not positive definite, mixconjugateblm issues a warning and replaces your specification with CorrelationPD, where:

CorrelationPD = 0.5*(Correlation + Correlation.');

For details on what value to specify for Correlation, see [1].

Data Types: double

A — Shape hyperparameter of inverse gamma prior on σ²

3 (default) | numeric scalar

Shape hyperparameter of the inverse gamma prior on σ², specified as a numeric scalar.

A must be at least –(Intercept + NumPredictors)/2.

With B held fixed, the inverse gamma distribution becomes taller and more concentrated as A increases. This characteristic weighs the prior model of σ² more heavily than the likelihood during posterior estimation.

For the functional form of the inverse gamma distribution, see Analytically Tractable Posteriors.

Example: 'A',0.1

Data Types: double

B — Scale hyperparameter of inverse gamma prior on σ²

1 (default) | positive scalar | Inf

Scale parameter of inverse gamma prior on σ², specified as a positive scalar or Inf.

With A held fixed, the inverse gamma distribution becomes taller and more concentrated as B increases. This characteristic weighs the prior model of σ² more heavily than the likelihood during posterior estimation.

Example: 'B',5

Data Types: double

Object Functions

estimate	Perform predictor variable selection for Bayesian linear regression models
simulate	Simulate regression coefficients and disturbance variance of Bayesian linear regression model
forecast	Forecast responses of Bayesian linear regression model
plot	Visualize prior and posterior densities of Bayesian linear regression model parameters
summarize	Distribution summary statistics of Bayesian linear regression model for predictor variable selection

Examples

Create Prior Model for SSVS

Consider the linear regression model that predicts the US real gross national product (GNPR) using a linear combination of industrial production index (IPI), total employment (E), and real wages (WR).

$${\text{GNPR}}_t={\beta }_0+{\beta }_1{\text{IPI}}_t+{\beta }_2{\text{E}}_t+{\beta }_3{\text{WR}}_t+{\epsilon }_t.$$

For all $$t$$, $${\epsilon }_t$$ is a series of independent Gaussian disturbances with a mean of 0 and variance $${\sigma }^2$$.

Assume these prior distributions for $\mathit{k}$ = 0,...,3:

• $${\beta }_k|{\sigma }^2,{\gamma }_k={\gamma }_k\sigma \sqrt{V_{k1}}{Z}_1+(1-{\gamma }_k)\sigma \sqrt{V_{k2}}{Z}_2$$, where ${\mathit{Z}}_1$ and ${\mathit{Z}}_2$ are independent, standard normal random variables. Therefore, the coefficients have a Gaussian mixture distribution. Assume all coefficients are conditionally independent, a priori, but they are dependent on the disturbance variance.

• $${\sigma }^2\sim IG(A,B)$$. $$A$$ and $$B$$ are the shape and scale, respectively, of an inverse gamma distribution.

• ${\gamma }_{\mathit{k}}\in \left\{0,1\right\}$and it represents the random variable-inclusion regime variable with a discrete uniform distribution.

Create a prior model for SSVS. Specify the number of predictors p.

p = 3;
PriorMdl = mixconjugateblm(p);

PriorMdl is a mixconjugateblm Bayesian linear regression model object representing the prior distribution of the regression coefficients and disturbance variance. mixconjugateblm displays a summary of the prior distributions at the command line.

Alternatively, you can create a prior model for SSVS by passing the number of predictors to bayeslm and setting the ModelType name-value pair argument to 'mixconjugate'.

MdlBayesLM = bayeslm(p,'ModelType','mixconjugate')

MdlBayesLM = 
  mixconjugateblm with properties:

    NumPredictors: 3
        Intercept: 1
         VarNames: {4x1 cell}
               Mu: [4x2 double]
                V: [4x2 double]
      Probability: [4x1 double]
      Correlation: [4x4 double]
                A: 3
                B: 1

 
           |  Mean     Std         CI95        Positive      Distribution     
------------------------------------------------------------------------------
 Intercept |  0      1.5890  [-3.547,  3.547]    0.500   Mixture distribution 
 Beta(1)   |  0      1.5890  [-3.547,  3.547]    0.500   Mixture distribution 
 Beta(2)   |  0      1.5890  [-3.547,  3.547]    0.500   Mixture distribution 
 Beta(3)   |  0      1.5890  [-3.547,  3.547]    0.500   Mixture distribution 
 Sigma2    | 0.5000  0.5000  [ 0.138,  1.616]    1.000   IG(3.00,    1)       
 

Mdl and MdlBayesLM are equivalent model objects.

You can set writable property values of created models using dot notation. Set the regression coefficient names to the corresponding variable names.

PriorMdl.VarNames = ["IPI" "E" "WR"]

PriorMdl = 
  mixconjugateblm with properties:

    NumPredictors: 3
        Intercept: 1
         VarNames: {4x1 cell}
               Mu: [4x2 double]
                V: [4x2 double]
      Probability: [4x1 double]
      Correlation: [4x4 double]
                A: 3
                B: 1

 
           |  Mean     Std         CI95        Positive      Distribution     
------------------------------------------------------------------------------
 Intercept |  0      1.5890  [-3.547,  3.547]    0.500   Mixture distribution 
 IPI       |  0      1.5890  [-3.547,  3.547]    0.500   Mixture distribution 
 E         |  0      1.5890  [-3.547,  3.547]    0.500   Mixture distribution 
 WR        |  0      1.5890  [-3.547,  3.547]    0.500   Mixture distribution 
 Sigma2    | 0.5000  0.5000  [ 0.138,  1.616]    1.000   IG(3.00,    1)       
 

MATLAB® associates the variable names to the regression coefficients in displays.

Plot the prior distributions.

plot(PriorMdl);

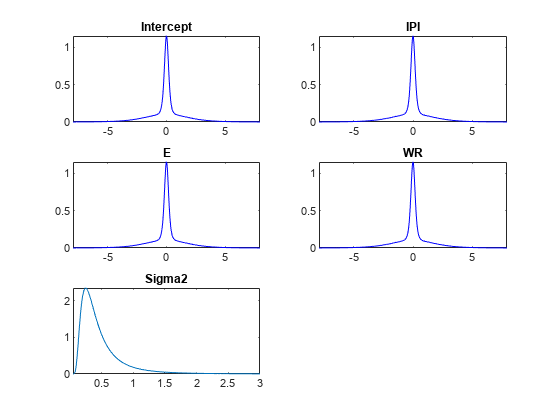
The prior distribution of each coefficient is a mixture of two Gaussians: both components have a mean of zero, but component 1 has a large variance relative to component 2. Therefore, their distributions are centered at zero and have the spike-and-slab appearance.

Perform Variable Selection Using SSVS and Default Options

Consider the linear regression model in Create Prior Model for SSVS.

Create a prior model for performing SSVS. Assume that $\beta$ and ${\sigma }^2$ are dependent (a conjugate mixture model). Specify the number of predictors p and the names of the regression coefficients.

p = 3;
PriorMdl = mixconjugateblm(p,'VarNames',["IPI" "E" "WR"]);

Display the prior regime probabilities and Gaussian mixture variance factors of the prior $\beta$.

priorProbabilities = table(PriorMdl.Probability,'RowNames',PriorMdl.VarNames,...
    'VariableNames',"Probability")

priorProbabilities=4×1 table
                 Probability
                 ___________

    Intercept        0.5    
    IPI              0.5    
    E                0.5    
    WR               0.5    

priorV = array2table(PriorMdl.V,'RowNames',PriorMdl.VarNames,...
    'VariableNames',["gammaIs1" "gammaIs0"])

priorV=4×2 table
                 gammaIs1    gammaIs0
                 ________    ________

    Intercept       10         0.1   
    IPI             10         0.1   
    E               10         0.1   
    WR              10         0.1   

PriorMdl stores prior regime probabilities in the Probability property and the regime variance factors in the V property. The default prior probability of variable inclusion is 0.5. The default variance factors for each coefficient are 10 for the variable-inclusion regime and 0.01 for the variable-exclusion regime.

Load the Nelson-Plosser data set. Create variables for the response and predictor series.

load Data_NelsonPlosser
X = DataTable{:,PriorMdl.VarNames(2:end)};
y = DataTable{:,'GNPR'};

Implement SSVS by estimating the marginal posterior distributions of $$\beta$$ and $${\sigma }^2$$. Because SSVS uses Markov chain Monte Carlo (MCMC) for estimation, set a random number seed to reproduce the results.

rng(1);
PosteriorMdl = estimate(PriorMdl,X,y);

Method: MCMC sampling with 10000 draws
Number of observations: 62
Number of predictors:   4
 
           |   Mean      Std           CI95        Positive  Distribution  Regime 
----------------------------------------------------------------------------------
 Intercept | -18.8333  10.1851  [-36.965,  0.716]    0.037     Empirical   0.8806 
 IPI       |   4.4554   0.1543   [ 4.165,  4.764]    1.000     Empirical   0.4545 
 E         |   0.0010   0.0004   [ 0.000,  0.002]    0.997     Empirical   0.0925 
 WR        |   2.4686   0.3615   [ 1.766,  3.197]    1.000     Empirical   0.1734 
 Sigma2    |  47.7557   8.6551   [33.858, 66.875]    1.000     Empirical    NaN   
 

PosteriorMdl is an empiricalblm model object that stores draws from the posterior distributions of $$\beta$$ and $${\sigma }^2$$ given the data. estimate displays a summary of the marginal posterior distributions at the command line. Rows of the summary correspond to regression coefficients and the disturbance variance, and columns correspond to characteristics of the posterior distribution. The characteristics include:

• CI95, which contains the 95% Bayesian equitailed credible intervals for the parameters. For example, the posterior probability that the regression coefficient of E (standardized) is in [0.000, 0.002] is 0.95.

• Regime, which contains the marginal posterior probability of variable inclusion ($\gamma =1$ for a variable). For example, the posterior probability that E should be included in the model is 0.0925.

Assuming, that variables with Regime < 0.1 should be removed from the model, the results suggest that you can exclude the unemployment rate from the model.

By default, estimate draws and discards a burn-in sample of size 5000. However, a good practice is to inspect a trace plot of the draws for adequate mixing and lack of transience. Plot a trace plot of the draws for each parameter. You can access the draws that compose the distribution (the properties BetaDraws and Sigma2Draws) using dot notation.

figure;
for j = 1:(p + 1)
    subplot(2,2,j);
    plot(PosteriorMdl.BetaDraws(j,:));
    title(sprintf('%s',PosteriorMdl.VarNames{j}));
end

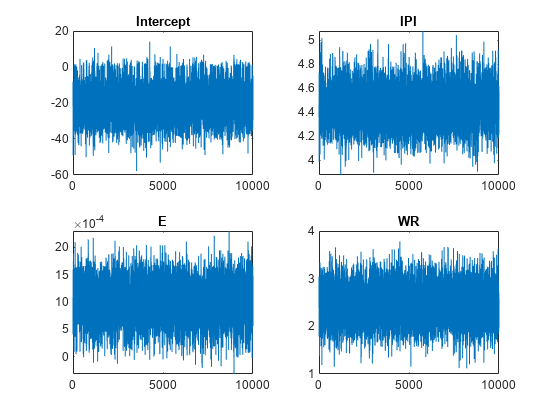
figure;
plot(PosteriorMdl.Sigma2Draws);
title('Sigma2');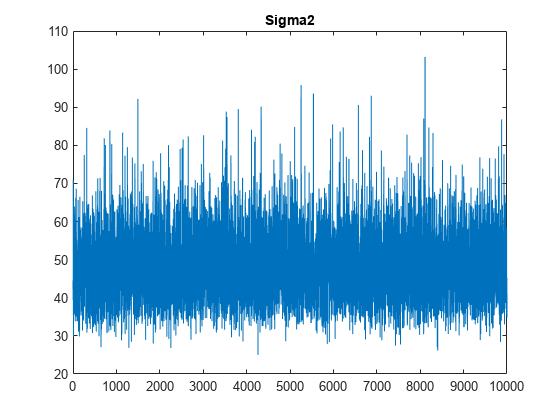

The trace plots indicate that the draws seem to mix well. The plots show no detectable transience or serial correlation, and the draws do not jump between states.

Specify Custom Prior Regime Probability Distribution for SSVS

Consider the linear regression model in Create Prior Model for SSVS.

Load the Nelson-Plosser data set. Create variables for the response and predictor series.

load Data_NelsonPlosser
VarNames = ["IPI" "E" "WR"];
X = DataTable{:,VarNames};
y = DataTable{:,"GNPR"};

Assume the following:

• The intercept is in the model with probability 0.9.

• IPI and E are in the model with probability 0.75.

• If E is included in the model, then the probability that WR is included in the model is 0.9.

• If E is excluded from the model, then the probability that WR is included is 0.25.

Declare a function named priorssvsexample.m that:

• Accepts a logical vector indicating whether the intercept and variables are in the model (true for model inclusion). Element 1 corresponds to the intercept, and the rest of the elements correspond to the variables in the data.

• Returns a numeric scalar representing the log of the described prior regime probability distribution.

function logprior = priorssvsexample(varinc)
%PRIORSSVSEXAMPLE Log prior regime probability distribution for SSVS
%   PRIORSSVSEXAMPLE is an example of a custom log prior regime probability
%   distribution for SSVS with dependent random variables. varinc is
%   a 4-by-1 logical vector indicating whether 4 coefficients are in a model
%   and logPrior is a numeric scalar representing the log of the prior
%   distribution of the regime probabilities.
%   
%   Coefficients enter a model according to these rules:
%       * varinc(1) is included with probability 0.9.
%       * varinc(2) and varinc(3) are in the model with probability 0.75.
%       * If varinc(3) is included in the model, then the probability that
%       varinc(4) is included in the model is 0.9.
%       * If varinc(3) is excluded from the model, then the probability
%       that varinc(4) is included is 0.25.

logprior = log(0.9) + 2*log(0.75) + log(varinc(3)*0.9 + (1-varinc(3))*0.25);

end

Create a prior model for performing SSVS. Assume that 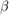and 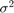are (a conjugate mixture model). Specify the number of predictors p the names of the regression coefficients, and custom, prior probability distribution of the variable-inclusion regimes.

p = 3;
PriorMdl = mixconjugateblm(p,'VarNames',["IPI" "E" "WR"],...
    'Probability',@priorssvsexample);

Implement SSVS by estimating the marginal posterior distributions of 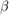and 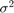. Because SSVS uses MCMC for estimation, set a random number seed to reproduce the results.

rng(1);
PosteriorMdl = estimate(PriorMdl,X,y);

Method: MCMC sampling with 10000 draws
Number of observations: 62
Number of predictors:   4
 
           |   Mean      Std           CI95        Positive  Distribution  Regime 
----------------------------------------------------------------------------------
 Intercept | -18.7971  10.1644  [-37.002,  0.765]    0.039     Empirical   0.8797 
 IPI       |   4.4559   0.1530   [ 4.166,  4.760]    1.000     Empirical   0.4623 
 E         |   0.0010   0.0004   [ 0.000,  0.002]    0.997     Empirical   0.2665 
 WR        |   2.4684   0.3618   [ 1.759,  3.196]    1.000     Empirical   0.1727 
 Sigma2    |  47.7391   8.6741   [33.823, 67.024]    1.000     Empirical    NaN   
 

Assuming, that variables with Regime < 0.1 should be removed from the model, the results suggest that you can include all variables in the model.

Forecast Responses Using Posterior Predictive Distribution

Consider the regression model in Create Prior Model for SSVS.

Perform SSVS:

1. Create a Bayesian regression model for SSVS with a conjugate prior for the data likelihood. Use the default settings.

2. Hold out the last 10 periods of data from estimation.

3. Estimate the marginal posterior distributions.

p = 3;
PriorMdl = bayeslm(p,'ModelType','mixconjugate','VarNames',["IPI" "E" "WR"]);

load Data_NelsonPlosser
fhs = 10; % Forecast horizon size
X = DataTable{1:(end - fhs),PriorMdl.VarNames(2:end)};
y = DataTable{1:(end - fhs),'GNPR'};
XF = DataTable{(end - fhs + 1):end,PriorMdl.VarNames(2:end)}; % Future predictor data
yFT = DataTable{(end - fhs + 1):end,'GNPR'};                  % True future responses

rng(1); % For reproducibility
PosteriorMdl = estimate(PriorMdl,X,y,'Display',false);

Forecast responses using the posterior predictive distribution and the future predictor data XF. Plot the true values of the response and the forecasted values.

yF = forecast(PosteriorMdl,XF);

figure;
plot(dates,DataTable.GNPR);
hold on
plot(dates((end - fhs + 1):end),yF)
h = gca;
hp = patch([dates(end - fhs + 1) dates(end) dates(end) dates(end - fhs + 1)],...
    h.YLim([1,1,2,2]),[0.8 0.8 0.8]);
uistack(hp,'bottom');
legend('Forecast Horizon','True GNPR','Forecasted GNPR','Location','NW')
title('Real Gross National Product: 1909 - 1970');
ylabel('rGNP');
xlabel('Year');
hold off

yF is a 10-by-1 vector of future values of real GNP corresponding to the future predictor data.

Estimate the forecast root mean squared error (RMSE).

frmse = sqrt(mean((yF - yFT).^2))

frmse = 
18.8470

The forecast RMSE is a relative measure of forecast accuracy. Specifically, you estimate several models using different assumptions. The model with the lowest forecast RMSE is the best-performing model of the ones being compared.

When you perform Bayesian regression with SSVS, a best practice is to tune the hyperparameters. One way to do so is to estimate the forecast RMSE over a grid of hyperparameter values, and choose the value that minimizes the forecast RMSE.

More About

Bayesian Linear Regression Model

A Bayesian linear regression model treats the parameters β and σ² in the multiple linear regression (MLR) model y_t = x_tβ + ε_t as random variables.

For times t = 1,...,T:

• y_t is the observed response.

• x_t is a 1-by-(p + 1) row vector of observed values of p predictors. To accommodate a model intercept, x_1t = 1 for all t.

• β is a (p + 1)-by-1 column vector of regression coefficients corresponding to the variables that compose the columns of x_t.

• ε_t is the random disturbance with a mean of zero and Cov(ε) = σ²I_T×T, while ε is a T-by-1 vector containing all disturbances. These assumptions imply that the data likelihood is

  $$\ell \left(\beta ,{\sigma }^2|y,x\right)={\displaystyle \prod _{t=1}^T\varphi \left(y_t;x_t\beta ,{\sigma }^2\right).}$$

  ϕ(y_t;x_tβ,σ²) is the Gaussian probability density with mean x_tβ and variance σ² evaluated at y_t;.

Before considering the data, you impose a joint prior distribution assumption on (β,σ²). In a Bayesian analysis, you update the distribution of the parameters by using information about the parameters obtained from the likelihood of the data. The result is the joint posterior distribution of (β,σ²) or the conditional posterior distributions of the parameters.

Stochastic Search Variable Selection

Stochastic search variable selection (SSVS) is a predictor variable selection method for Bayesian linear regression that searches the space of potential models for models with high posterior probability, and averages the models it finds after it completes the search.

SSVS assumes that the prior distribution of each regression coefficient is a mixture of two Gaussian distributions, and the prior distribution of σ² is inverse gamma with shape A and scale B. Let γ = {γ₁,…,γ_K} be a latent, random regime indicator for the regression coefficients β, where:

• K is the number of coefficients in the model (Intercept + NumPredictors). γ_k = 1 means that β_k|σ²,γ_k is Gaussian with mean 0 and variance c₁.

• γ_k = 0 means that a predictor is Gaussian with mean 0 and variance c₂.

• A probability mass function governs the distribution of γ, and the sample space of γ is composed of 2^K elements.

More specifically, given γ_k and σ², β_k = γ_kc₁Z + (1 – γ_k)c₂Z, where:

• Z is a standard normal random variable.

• For conjugate models (mixconjugateblm), c_j = σ²V_j, j = 1,2.

• For semiconjugate models (mixsemiconjugateblm), c_j = V_j.

c₁ is relatively large, which implies that the corresponding predictor is more likely to be in the model. c₂ is relatively small, which implies that the corresponding predictor is less likely to be in the model because distribution is dense around 0.

In this framework, if the potential exists for a total of K coefficients in a model, then the space has 2^K models through which to search. Because computing posterior probabilities of all 2^K models can be computationally expensive, SSVS uses MCMC to sample γ = {γ₁,…,γ_K} and estimate posterior probabilities of corresponding models. The models that the algorithm chooses often have higher posterior probabilities. The algorithm composes the estimated posterior distributions of β and σ² by computing the weighted average of the sampled models. The algorithm attributes a larger weight to those models sampled more often.

The resulting posterior distribution for conjugate mixture models is analytically tractable (see Algorithms). For details on the posterior distribution, see Analytically Tractable Posteriors.

Algorithms

A closed-form posterior exists for conjugate mixture priors in the SSVS framework with K coefficients. However, because the prior β|σ²,γ, marginalized by γ, is a 2^K-component Gaussian mixture, MATLAB^® uses MCMC instead to sample from the posterior for numerical stability.

Alternative Functionality

The bayeslm function can create any supported prior model object for Bayesian linear regression.

References

[1] George, E. I., and R. E. McCulloch. "Variable Selection Via Gibbs Sampling." Journal of the American Statistical Association. Vol. 88, No. 423, 1993, pp. 881–889.

[2] Koop, G., D. J. Poirier, and J. L. Tobias. Bayesian Econometric Methods. New York, NY: Cambridge University Press, 2007.

Version History

Introduced in R2018b