simsmooth
Simulation smoother of Bayesian vector autoregression (VAR) model
Syntax
Description
simsmooth is well suited for advanced applications, such as out-of-sample conditional forecasting from the posterior predictive distribution of a Bayesian VAR(p) model, VARX(p) model forecasting, missing value imputation, and parameter estimation in the presence of missing values. Also, simsmooth enables you to adjust the Gibbs sampler for out-of-sample forecasting. To estimate out-of-sample forecasts from a Bayesian VAR(p) model, see forecast.
[ returns 1000 random draws of coefficient vectors λ
CoeffDraws,SigmaDraws] = simsmooth(PriorMdl,Y)Coeff and innovations covariance matrices Σ Sigma, drawn from the posterior distribution formed by combining the prior Bayesian VAR(p) model
PriorMdl and the response data Y.
The sampling procedure includes a Bayesian data augmentation step that uses the Kalman filter (see Algorithms). During sampling, simsmooth replaces non-presample missing values in Y, indicated by NaN values, with imputed values.
[ uses additional options specified by one or more name-value pair arguments. For example, you can set the number of random draws from the distribution or specify the presample response data.CoeffDraws,SigmaDraws] = simsmooth(PriorMdl,Y,Name,Value)
[ also returns the imputed response values of each draw CoeffDraws,SigmaDraws,NaNDraws]
= simsmooth(___)NaNDraws using any of the input argument combinations in the previous syntaxes.
[ also returns the mean CoeffDraws,SigmaDraws,NaNDraws,YMean,YStd]
= simsmooth(___)YMean and standard deviation YStd of the posterior predictive distribution of the augmented data.
Examples
When simulate estimates the posterior distribution from which to draw parameters, it removes all rows in the data that contain at least one missing value (NaN). However, simsmooth uses Bayesian data augmentation to impute non-presample missing values during posterior estimation.
Consider the 3-D VAR(4) model for the US inflation (INFL), unemployment (UNRATE), and federal funds (FEDFUNDS) rates.
For all , is a series of independent 3-D normal innovations with a mean of 0 and covariance . Assume a weak conjugate prior distribution for the parameters .
Load and Preprocess Data
Load the US macroeconomic data set. Compute the inflation rate, and stabilize the unemployment and federal funds rates.
load Data_USEconModel seriesnames = ["INFL" "UNRATE" "FEDFUNDS"]; DataTimeTable.INFL = 100*[NaN; price2ret(DataTimeTable.CPIAUCSL)]; DataTimeTable.DUNRATE = [NaN; diff(DataTimeTable.UNRATE)]; DataTimeTable.DFEDFUNDS = [NaN; diff(DataTimeTable.FEDFUNDS)]; seriesnames(2:3) = "D" + seriesnames(2:3);
Several series have leading NaN values because their measurements were not available at the same time as other measurements. Because leading NaN values can interfere with presample specification, remove all rows containing at least one leading missing value.
rmldDataTimeTable = rmmissing(DataTimeTable(:,seriesnames));
Create Prior Model
Create a weak conjugate prior model by specifying large coefficient prior variances. Specify the response series names.
numseries = numel(seriesnames);
numlags = 4;
PriorMdl = conjugatebvarm(numseries,numlags,'SeriesNames',seriesnames);
numcoeffseqn = size(PriorMdl.V,1);
PriorMdl.V = 1e4*eye(numcoeffseqn);Randomly Place Missing Values in Data
To illustrate simulation in the presence of missing values, randomly place missing values in the data after the presample period.
rng(1) % For reproducibility T = size(rmldDataTimeTable,1); idxpre = 1:PriorMdl.P; % Presample period idxest = (PriorMdl.P + 1):T; % Estimation period nmissing = 20; % Simulate at most nmissing missing values sidx = [randsample(idxest,nmissing,true); randsample(1:numseries,nmissing,true)]; lsidx = sub2ind([T,numseries],sidx(1,:),sidx(2,:)); MissData = table2array(rmldDataTimeTable); MissData(lsidx) = NaN; MissDataTimeTable = rmldDataTimeTable; MissDataTimeTable{:,:} = MissData;
Simulate Parameters from Posterior
Draw 1000 parameter sets from the posterior distribution by calling simsmooth, which estimates the posterior distribution of the parameters, and then forms the posterior predictive distribution.
[Coeff,Sigma] = simsmooth(PriorMdl,MissDataTimeTable.Variables);
Coeff is a 39-by-1000 matrix of randomly drawn coefficient vectors from the posterior. Sigma is a 3-by-3-by-1000 array of randomly drawn innovations covariance matrices.
By default, simsmooth initializes the VAR model by using the first four observations in the data.
To associate rows of Coeff to coefficients, obtain a summary of the prior distribution by using summarize. In a table, display the first set of randomly drawn coefficients with corresponding names.
Summary = summarize(PriorMdl,'off'); table(Coeff(:,1),'RowNames',Summary.CoeffMap)
ans=39×1 table
Var1
__________
AR{1}(1,1) 0.22109
AR{1}(1,2) -0.24034
AR{1}(1,3) 0.093315
AR{2}(1,1) 0.18329
AR{2}(1,2) -0.23178
AR{2}(1,3) -0.026301
AR{3}(1,1) 0.39991
AR{3}(1,2) 0.41141
AR{3}(1,3) 0.054702
AR{4}(1,1) 0.024944
AR{4}(1,2) -0.37372
AR{4}(1,3) -0.0095642
Constant(1) 0.21499
AR{1}(2,1) -0.073776
AR{1}(2,2) 0.36086
AR{1}(2,3) 0.071088
⋮
Alternatively, you can create an empirical model from the draws, and use summarize to display the model by specifying any display option.
Display a summary of the posterior draws as an equation.
EmpMdl = empiricalbvarm(numseries,numlags,'SeriesNames',seriesnames,... 'CoeffDraws',Coeff,'SigmaDraws',Sigma); summarize(EmpMdl,'equation')
VAR Equations
| INFL(-1) DUNRATE(-1) DFEDFUNDS(-1) INFL(-2) DUNRATE(-2) DFEDFUNDS(-2) INFL(-3) DUNRATE(-3) DFEDFUNDS(-3) INFL(-4) DUNRATE(-4) DFEDFUNDS(-4) Constant
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
INFL | 0.1447 -0.3685 0.1013 0.2974 -0.0959 0.0360 0.4115 0.2244 0.0474 0.0265 -0.2321 0.0030 0.1095
| (0.0744) (0.1314) (0.0370) (0.0833) (0.1509) (0.0398) (0.0833) (0.1440) (0.0403) (0.0879) (0.1301) (0.0370) (0.0744)
DUNRATE | -0.0187 0.4445 0.0314 0.0836 0.2372 0.0489 -0.0407 -0.0548 -0.0064 0.0483 -0.1753 0.0027 -0.0597
| (0.0447) (0.0808) (0.0234) (0.0514) (0.0863) (0.0230) (0.0507) (0.0906) (0.0243) (0.0514) (0.0779) (0.0225) (0.0466)
DFEDFUNDS | -0.2046 -1.1927 -0.2524 0.2864 -0.2282 -0.2657 0.2709 -0.6231 0.0289 -0.0404 0.1043 -0.1236 -0.2952
| (0.1530) (0.2931) (0.0816) (0.1832) (0.3123) (0.0857) (0.1736) (0.3105) (0.0900) (0.1866) (0.2880) (0.0758) (0.1684)
Innovations Covariance Matrix
| INFL DUNRATE DFEDFUNDS
-------------------------------------------
INFL | 0.2842 -0.0098 0.1346
| (0.0286) (0.0122) (0.0464)
DUNRATE | -0.0098 0.1062 -0.1496
| (0.0122) (0.0106) (0.0296)
DFEDFUNDS | 0.1346 -0.1496 1.3187
| (0.0464) (0.0296) (0.1422)
Consider the 3-D VAR(4) model of Simulate Parameters from Posterior Distribution in Presence of Missing Values.
Load the US macroeconomic data set. Compute the inflation rate, and stabilize the unemployment and federal funds rates.
load Data_USEconModel seriesnames = ["INFL" "UNRATE" "FEDFUNDS"]; DataTimeTable.INFL = 100*[NaN; price2ret(DataTimeTable.CPIAUCSL)]; DataTimeTable.DUNRATE = [NaN; diff(DataTimeTable.UNRATE)]; DataTimeTable.DFEDFUNDS = [NaN; diff(DataTimeTable.FEDFUNDS)]; seriesnames(2:3) = "D" + seriesnames(2:3);
Remove all rows that contain leading missing values.
rmldDataTimeTable = rmmissing(DataTimeTable(:,seriesnames));
Create a weak conjugate prior model. Specify the response series names.
numseries = numel(seriesnames);
numlags = 4;
PriorMdl = conjugatebvarm(numseries,numlags,'SeriesNames',seriesnames);
numcoeffseqn = size(PriorMdl.V,1);
PriorMdl.V = 1e4*eye(numcoeffseqn);Randomly place missing values in the data after the presample period.
rng(1) % For reproducibility T = size(rmldDataTimeTable,1); idxpre = 1:PriorMdl.P; % Presample period idxest = (PriorMdl.P + 1):T; % Estimation period nmissing = 20; % Simulate at most nmissing missing values sidx = [randsample(idxest,nmissing,true); randsample(1:numseries,nmissing,true)]; lsidx = sub2ind([T,numseries],sidx(1,:),sidx(2,:)); MissData = table2array(rmldDataTimeTable); MissData(lsidx) = NaN; MissDataTimeTable = rmldDataTimeTable; MissDataTimeTable{:,:} = MissData;
Draw 1000 parameter sets from the posterior distribution by calling simsmooth. Return the values that the simulation smoother imputes for the missing observations.
[~,~,NaNDraws] = simsmooth(PriorMdl,MissDataTimeTable.Variables);
NaNDraws is a 19-by-1000 matrix of randomly drawn response vectors from the posterior predictive distribution. Elements correspond to the missing values in the data ordered by a column-wise search. For example, NaNDraws(3,1) is the first randomly drawn imputed response of the third missing value in the data. Find the corresponding value in the data.
[idxi,idxj] = find(ismissing(MissDataTimeTable),3); responsename = seriesnames(idxj(end))
responsename = "INFL"
observationtime = MissDataTimeTable.Time(idxi(end))
observationtime = datetime
Q3-65
Plot the empirical distribution of the imputed values of the inflation rate during Q3-65.
histogram(NaNDraws(3,:))
title('Q3-65 Inflation Rate Empirical Distribution')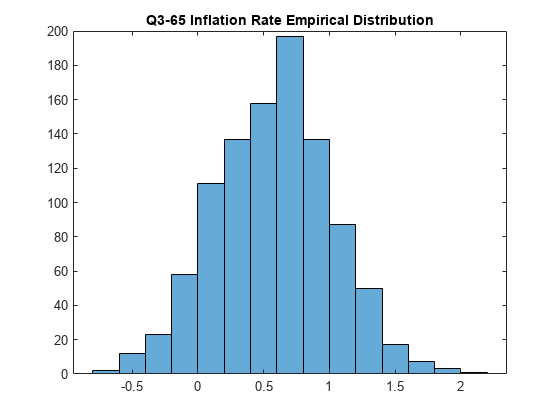
Consider the 3-D VAR(4) model of Simulate Parameters from Posterior Distribution in Presence of Missing Values.
Load the US macroeconomic data set. Compute the inflation rate, stabilize the unemployment and federal funds rates, and remove missing values (the data includes leading missing values only).
load Data_USEconModel seriesnames = ["INFL" "UNRATE" "FEDFUNDS"]; DataTimeTable.INFL = 100*[NaN; price2ret(DataTimeTable.CPIAUCSL)]; DataTimeTable.DUNRATE = [NaN; diff(DataTimeTable.UNRATE)]; DataTimeTable.DFEDFUNDS = [NaN; diff(DataTimeTable.FEDFUNDS)]; seriesnames(2:3) = "D" + seriesnames(2:3); rmDataTimeTable = rmmissing(DataTimeTable);
Create a weak conjugate prior model. Specify the response series names.
numseries = numel(seriesnames);
numlags = 4;
PriorMdl = conjugatebvarm(numseries,numlags,'SeriesNames',seriesnames);
numcoeffseqn = size(PriorMdl.V,1);
PriorMdl.V = 1e4*eye(numcoeffseqn);Simulate 5000 coefficients and innovations covariance matrices from the posterior distribution. Specify a burn-in period of 1000 and a thinning factor of 5.
rng(1); % For reproducibility [Coeff,Sigma] = simsmooth(PriorMdl,rmDataTimeTable{:,seriesnames},... 'NumDraws',5000,'BurnIn',1000,'Thin',5);
Coeff is a 39-by-5000 matrix of coefficients, and Sigma is a 3-by-3-by-5000 array of innovations covariance matrices. Both Coeff and Sigma are randomly drawn from the posterior distribution.
Consider the 3-D VAR(4) model of Simulate Parameters from Posterior Distribution in Presence of Missing Values. In this case, assume that the prior model is semiconjugate.
Load the US macroeconomic data set. Compute the inflation rate, stabilize the unemployment and federal funds rates, and remove missing values (the data includes leading missing values only).
load Data_USEconModel seriesnames = ["INFL" "UNRATE" "FEDFUNDS"]; DataTimeTable.INFL = 100*[NaN; price2ret(DataTimeTable.CPIAUCSL)]; DataTimeTable.DUNRATE = [NaN; diff(DataTimeTable.UNRATE)]; DataTimeTable.DFEDFUNDS = [NaN; diff(DataTimeTable.FEDFUNDS)]; seriesnames(2:3) = "D" + seriesnames(2:3); rmDataTimeTable = rmmissing(DataTimeTable);
Create a semiconjugate prior model. Specify the response series names.
numseries = numel(seriesnames); numlags = 4; PriorMdl = bayesvarm(numseries,numlags,'ModelType','semiconjugate',... 'SeriesNames',seriesnames);
To obtain starting values for the coefficients, consider the coefficients from a VAR model fitted to the first 30 observations.
Define index sets that partition the data into four sets:
Length p = 4 initialization period for the dynamic component of the model
= 30 observations to estimate the VAR for the coefficient initial values
Length p = 4 initialization period for the dynamic component of the Bayesian VAR model
Remaining observations to estimate the posterior
T = height(rmDataTimeTable); n0 = 30; idxpre0 = 1:PriorMdl.P; idxest0 = (idxpre0(end) + 1):(idxpre0(end) + 1 + n0); idxpre1 = (idxest0(end) + 1 - PriorMdl.P):idxest0(end); idxest1 = (idxest0(end) + 1):T; n1 = numel(idxest1);
Obtain initial coefficient values by fitting a VAR model to the first 34 observations. Use the first four observations as a presample.
Mdl0 = varm(PriorMdl.NumSeries,PriorMdl.P);
EstMdl0 = estimate(Mdl0,rmDataTimeTable{idxest0,seriesnames},'Y0',rmDataTimeTable{idxpre0,seriesnames});estimate returns a model object containing the AR coefficient estimates in matrix form and the constants in a vector. The Bayesian VAR functions require initial coefficient values in a vector. Format the initial coefficient values.
Coeff0 = [EstMdl0.AR{:} EstMdl0.Constant].';
Coeff0 = Coeff0(:);Simulate 1000 coefficients and innovations covariance matrices from the posterior distribution. Specify the remaining observations from which to estimate the posterior. Initialize the VAR model by specifying the last four observations in the previous estimation sample as a presample, and specify the initial coefficient vector to initialize the posterior sample.
rng(1) % For reproducibility [Coeff,Sigma] = simsmooth(PriorMdl,rmDataTimeTable{idxest1,seriesnames},... 'Y0',rmDataTimeTable{idxpre1,seriesnames},'Coeff0',Coeff0);
Coeff is a 39-by-1000 matrix of coefficients and Sigma is a 3-by-3-by-1000 array of innovations covariance matrices. Both Coeff and Sigma are randomly drawn from the posterior distribution.
Consider the 3-D VAR(4) model of Simulate Parameters from Posterior Distribution in Presence of Missing Values.
Load and Preprocess Data
Load the US macroeconomic data set. Compute the inflation rate, stabilize the unemployment and federal funds rates, and remove missing values (the data includes leading missing values only).
load Data_USEconModel seriesnames = ["INFL" "UNRATE" "FEDFUNDS"]; DataTimeTable.INFL = 100*[NaN; price2ret(DataTimeTable.CPIAUCSL)]; DataTimeTable.DUNRATE = [NaN; diff(DataTimeTable.UNRATE)]; DataTimeTable.DFEDFUNDS = [NaN; diff(DataTimeTable.FEDFUNDS)]; seriesnames(2:3) = "D" + seriesnames(2:3); rmDataTimeTable = rmmissing(DataTimeTable);
Create Prior Model
Create a weak conjugate prior model. Specify the response series names.
numseries = numel(seriesnames);
numlags = 4;
PriorMdl = conjugatebvarm(numseries,numlags,'SeriesNames',seriesnames);
numcoeffseqn = size(PriorMdl.V,1);
PriorMdl.V = 1e4*eye(numcoeffseqn);Forecast Responses Using forecast
Directly forecast two years (eight quarters) of observations from the posterior predictive distribution. forecast estimates the posterior distribution of the parameters, and then forms the posterior predictive distribution.
rng(1); % For reproducibility
numperiods = 8;
YF = forecast(PriorMdl,numperiods,rmDataTimeTable{:,seriesnames});YF is an 8-by-3 matrix of forecasted responses.
Plot the forecasted responses.
fh = rmDataTimeTable.Time(end) + calquarters(1:8); for j = 1:PriorMdl.NumSeries subplot(3,1,j) plot(rmDataTimeTable.Time(end - 20:end),rmDataTimeTable{end - 20:end,seriesnames(j)},'r',... [rmDataTimeTable.Time(end) fh],[rmDataTimeTable{end,seriesnames(j)}; YF(:,j)],'b'); legend("Observed","Forecasted",'Location','NorthWest') title(seriesnames(j)) end
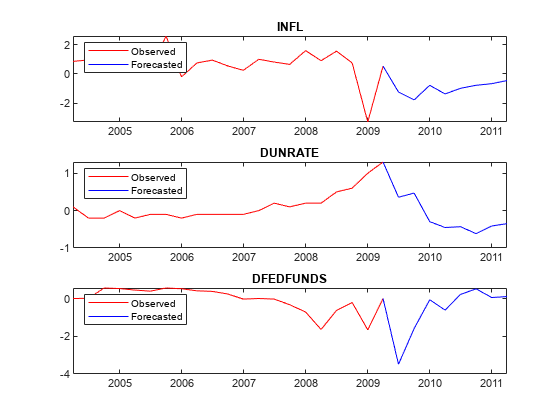
Forecast Responses Using simsmooth
Configure the data set for obtaining forecasts from simsmooth by concatenating a numperiods-by-numseries timetable of missing values to the end of the set.
fTT = array2timetable(NaN(numperiods,numseries),'RowTimes',fh,... 'VariableNames',seriesnames); frmDataTimeTable = [rmDataTimeTable(:,seriesnames); fTT]; tail(frmDataTimeTable)
Time INFL DUNRATE DFEDFUNDS
_____ ____ _______ _________
Q2-09 NaN NaN NaN
Q3-09 NaN NaN NaN
Q4-09 NaN NaN NaN
Q1-10 NaN NaN NaN
Q2-10 NaN NaN NaN
Q3-10 NaN NaN NaN
Q4-10 NaN NaN NaN
Q1-11 NaN NaN NaN
Forecast the VAR model using simsmooth. Like forecast, simsmooth estimates the posterior distribution, so it requires a prior model and data. Specify the data containing the trailing NaNs.
[~,~,~,YMean] = simsmooth(PriorMdl,frmDataTimeTable.Variables);
YMean is almost equal to frmDataTimeTable, with these exceptions:
YMeanexcludes rows corresponding to the presample periodfrmDataTimeTable(1:4,:).If
frmDataTimeTable(j,k)isNaN,YMean(j,k)is the mean of the posterior predictive distribution of responsekat timej.
Create a timetable from YMean.
YMeanTT = array2timetable(YMean,'RowTimes',frmDataTimeTable.Time((PriorMdl.P + 1):end),... 'VariableNames',seriesnames);
Plot the forecasted responses.
tiledlayout(3,1) for j = 1:PriorMdl.NumSeries nexttile plot(YMeanTT.Time((end - 20 - numperiods):(end - numperiods)),YMeanTT{(end - 20 - numperiods):(end - numperiods),j},'r',... YMeanTT.Time((end - numperiods):end),YMeanTT{(end - numperiods):end,j},'b'); legend("Observed","Forecasted",'Location','NorthWest') title(seriesnames(j)) end

Consider the 3-D VAR(4) model of Simulate Parameters from Posterior Distribution in Presence of Missing Values.
Load the US macroeconomic data set. Compute the inflation rate, stabilize the unemployment and federal funds rates, and remove missing values (the data includes leading missing values only).
load Data_USEconModel seriesnames = ["INFL" "UNRATE" "FEDFUNDS"]; DataTimeTable.INFL = 100*[NaN; price2ret(DataTimeTable.CPIAUCSL)]; DataTimeTable.DUNRATE = [NaN; diff(DataTimeTable.UNRATE)]; DataTimeTable.DFEDFUNDS = [NaN; diff(DataTimeTable.FEDFUNDS)]; seriesnames(2:3) = "D" + seriesnames(2:3); rmDataTimeTable = rmmissing(DataTimeTable);
Create a weak conjugate prior model. Specify the response series names.
numseries = numel(seriesnames);
numlags = 4;
PriorMdl = conjugatebvarm(numseries,numlags,'SeriesNames',seriesnames);
numcoeffseqn = size(PriorMdl.V,1);
PriorMdl.V = 1e4*eye(numcoeffseqn);Conditional forecasting occurs when response values are known or hypothesized in the forecast horizon, and unknown values are forecasted conditioned on the known values. Suppose that the unemployment rate change (DUNRATE) remains at one percentage point through a two-year forecast horizon.
Configure the data set for obtaining forecasts from simsmooth by concatenating a numperiods-by-numseries timetable of missing values to the end of the set. For the unemployment rate change, replace the missing values with a vector of ones.
rng(1); % For reproducibility numperiods = 8; fh = rmDataTimeTable.Time(end) + calquarters(1:8); fTT = array2timetable(NaN(numperiods,numseries),'RowTimes',fh,... 'VariableNames',seriesnames); frmDataTimeTable = [rmDataTimeTable(:,seriesnames); fTT]; frmDataTimeTable.DUNRATE((end - numperiods + 1):end) = ones(numperiods,1); tail(frmDataTimeTable)
Time INFL DUNRATE DFEDFUNDS
_____ ____ _______ _________
Q2-09 NaN 1 NaN
Q3-09 NaN 1 NaN
Q4-09 NaN 1 NaN
Q1-10 NaN 1 NaN
Q2-10 NaN 1 NaN
Q3-10 NaN 1 NaN
Q4-10 NaN 1 NaN
Q1-11 NaN 1 NaN
Obtain forecasts for the inflation rate and federal funds rate change series, given that the unemployment rate change is one for the entire horizon.
[~,~,~,YMean] = simsmooth(PriorMdl,frmDataTimeTable.Variables);
YMean is almost equal to frmDataTimeTable, with these exceptions:
YMeanexcludes rows corresponding to the presample periodfrmDataTimeTable(1:4,:).If
frmDataTimeTable(j,k)isNaN,YMean(j,k)is the mean of the posterior predictive distribution of responsekat timej.
Create a timetable from YMean.
YMeanTT = array2timetable(YMean,'RowTimes',frmDataTimeTable.Time((PriorMdl.P + 1):end),... 'VariableNames',seriesnames);
Plot the forecasted responses.
for j = 1:PriorMdl.NumSeries subplot(3,1,j) plot(YMeanTT.Time((end - 20 - numperiods):(end - numperiods)),YMeanTT{(end - 20 - numperiods):(end - numperiods),j},'r',... YMeanTT.Time((end - numperiods):end),YMeanTT{(end - numperiods):end,j},'b'); legend("Observed","Forecasted",'Location','NorthWest') title(seriesnames(j)) end
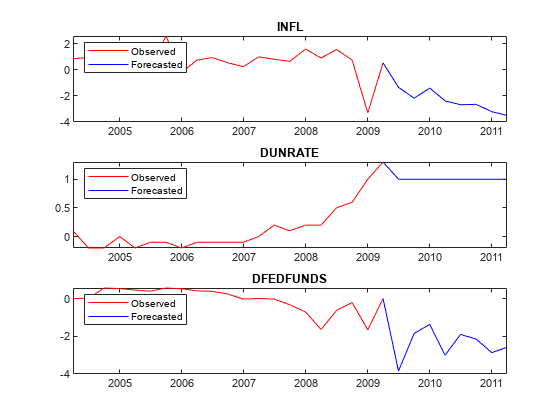
Consider the 2-D VARX(1) model for the US real GDP (RGDP) and investment (GCE) rates that treats the personal consumption (PCEC) rate as exogenous:
For all , is a series of independent 2-D normal innovations with a mean of 0 and covariance . Assume the following prior distributions:
, where M is a 4-by-2 matrix of means and is the 4-by-4 among-coefficient scale matrix. Equivalently, .
where Ω is the 2-by-2 scale matrix and is the degrees of freedom.
Load the US macroeconomic data set. Compute the real GDP, investment, and personal consumption rate series. Remove all missing values from the resulting series.
load Data_USEconModel DataTimeTable.RGDP = DataTimeTable.GDP./DataTimeTable.GDPDEF; seriesnames = ["PCEC"; "RGDP"; "GCE"]; rates = varfun(@price2ret,DataTimeTable,'InputVariables',seriesnames); rates = rmmissing(rates); rates.Properties.VariableNames = seriesnames;
Create a conjugate prior model for the 2-D VARX(1) model parameters.
numseries = 2; numlags = 1; numpredictors = 1; PriorMdl = conjugatebvarm(numseries,numlags,'NumPredictors',numpredictors,... 'SeriesNames',seriesnames(2:end));
Create index sets that partition the data into estimation and forecast samples. Specify a forecast horizon of two years.
T = size(rates,1);
numperiods = 8;
idxest = 1:(T - numperiods); % Includes presample
idxf = (T - numperiods + 1):T;
idxtot = [idxest idxf];The simulation smoother forecasts by imputing missing values. Therefore, create a data set that contains missing values for the responses in the forecast horizon.
missingrates = rates;
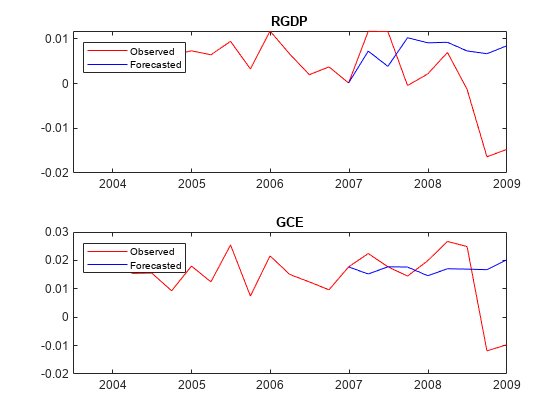
missingrates{idxf,PriorMdl.SeriesNames} = nan(numperiods,PriorMdl.NumSeries);Forecast responses in the forecast horizon. Specify presample observations and the exogenous predictor data. Return standard deviations of the posterior predictive distribution.
rng(1) % For reproducibility [~,~,~,YMean,YStd] = simsmooth(PriorMdl,missingrates{:,PriorMdl.SeriesNames},... 'X',missingrates{:,seriesnames(1)});
Create a timetable from YMean.
YMeanTT = array2timetable(YMean,'RowTimes',rates.Time((PriorMdl.P + 1):end),... 'VariableNames',PriorMdl.SeriesNames);
Plot the forecasted responses.
tiledlayout(2,1) for j = 1:PriorMdl.NumSeries nexttile plot(rates.Time((end - 20):end),rates{(end - 20):end,PriorMdl.SeriesNames(j)},'r',... YMeanTT.Time((end - numperiods):end),YMeanTT{(end - numperiods):end,PriorMdl.SeriesNames(j)},'b'); legend("Observed","Forecasted",'Location','NorthWest') title(PriorMdl.SeriesNames(j)) end
Input Arguments
Prior Bayesian VAR model, specified as a model object in this table.
| Model Object | Description |
|---|---|
conjugatebvarm | Dependent, matrix-normal-inverse-Wishart conjugate model returned by bayesvarm, conjugatebvarm, or estimate |
semiconjugatebvarm | Independent, normal-inverse-Wishart semiconjugate prior model returned by bayesvarm or semiconjugatebvarm |
diffusebvarm | Diffuse prior model returned by bayesvarm or diffusebvarm |
normalbvarm | Normal conjugate model with a fixed innovations covariance matrix, returned by bayesvarm, normalbvarm, or estimate |
Observed multivariate response series to which simsmooth fits the model, specified as a numobs-by-numseries numeric matrix.
numobs is the sample size. numseries is the number of response variables (PriorMdl.NumSeries).
Rows correspond to observations, and the last row contains the latest observation. Columns correspond to individual response variables.
NaN values in Y indicate missing observations. simsmooth replaces non-presample missing values with an imputation (see NaNDraws) as part of the sampling process.
Y represents the continuation of the presample response series Y0.
Tip
To obtain
numperiodsout-of-sample forecasts, concatenate anumperiods-by-numseriesmatrix ofNaNs to the end ofY.simsmoothreturns the forecasts and standard deviations in the corresponding elements ofYMeanandYStd, respectively. For example:numperiods = 8; Y = [Y; NaN(numperiods,PriorMdl.NumSeries)];
To obtain forecasts conditioned on observed (or hypothesized) values in a forecast horizon, concatenate a
numperiods-by-numseriesmatrix ofNaNs and observed or hypothesized values to the end ofY. For example, in a 2-D system, obtain the one-step-ahead forecast of response variable 1, given that response variable 2 is 0.5, by specifyingY = [Y; [NaN 0.5]];
Data Types: double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'Y0',Y0,'X',X specifies the presample response data Y0 to initialize the VAR model for posterior simulation, and the predictor data X for the exogenous regression component.
Presample response data to initialize the VAR model for simulation, specified as the comma-separated pair consisting of 'Y0' and a numpreobs-by-numseries numeric matrix. numpreobs is the number of presample observations.
Rows correspond to presample observations, and the last row contains the latest observation. Y0 must have at least PriorMdl.P rows. If you supply more rows than necessary, simsmooth uses the latest PriorMdl.P observations only.
Columns must correspond to the response series in Y.
By default, simsmooth uses Y(1:PriorMdl.P,:) as presample observations, and then estimates the posterior using Y((PriorMdl.P + 1):end,:). This action reduces the effective sample size. The number of rows of the outputs YMean and YStd is size(Y,1) – PriorMdl.P. If Y0 contains at least one NaN, simsmooth issues an error.
Data Types: double
Predictor data for the exogenous regression component in the model, specified as the comma-separated pair consisting of 'X' and a numobs-by-PriorMdl.NumPredictors numeric matrix.
Rows correspond to observations, and the last row contains the latest observation. simsmooth does not use the regression component in the presample period. X must have at least as many observations as the observations used after the presample period.
In either case, if you supply more rows than necessary, simsmooth uses the latest observations only.
Columns correspond to individual predictor variables. All predictor variables are present in the regression component of each response equation.
If X contains at least one NaN, simsmooth issues an error.
Data Types: double
Number of random draws from the distributions, specified as the comma-separated pair consisting of 'NumDraws' and a positive integer.
Example: 'NumDraws',1e7
Data Types: double
Number of draws to remove from the beginning of the sample to reduce transient effects, specified as the comma-separated pair consisting of 'BurnIn' and a nonnegative scalar. For details on how simsmooth reduces the full sample, see Algorithms.
Tip
To help you specify the appropriate burn-in period size:
Determine the extent of the transient behavior in the sample by specifying
'BurnIn',0.Simulate a few thousand observations by using
simsmooth.Draw trace plots.
Example: 'BurnIn',0
Data Types: double
Adjusted sample size multiplier, specified as the comma-separated pair consisting of 'Thin' and a positive integer.
The actual sample size is BurnIn + NumDraws*Thin. After discarding the burn-in, simsmooth discards every Thin – 1 draws, and then retains the next draw. For more details on how simsmooth reduces the full sample, see Algorithms.
Tip
To reduce potential large serial correlation in the sample, or to reduce the memory consumption of the draws stored in PriorMdl, specify a large value for Thin.
Example: 'Thin',5
Data Types: double
Starting value of the VAR model coefficients for the Gibbs sampler, specified as the comma-separated pair consisting of 'Coeff0' and a numeric column vector with (Mdl.NumSeries*)-by-kNumDraws elements, where k = Mdl.NumSeries*Mdl.P + Mdl.IncludeIntercept + Mdl.IncludeTrend + Mdl.NumPredictorsCoeff0, see the output CoeffDraws.
By default, Coeff0 is the multivariate least-squares estimate.
Tip
To specify
Coeff0:Set separate variables for the initial values of each coefficient matrix and vector.
Horizontally concatenate all coefficient means in this order:
Vectorize the transpose of the coefficient mean matrix.
Coeff0 = Coeff.'; Coeff0 = Coeff0(:);
A good practice is to run
simsmoothmultiple times with different parameter starting values. Verify that the estimates from each run converge to similar values.
Data Types: double
Starting value of the innovations covariance matrix for the Gibbs sampler, specified as the comma-separated pair consisting of 'Sigma0' and a PriorMdl.NumSeries-by-PriorMdl.NumSeries positive definite numeric matrix. By default, Sigma0 is the residual mean squared error from multivariate least-squares. Rows and columns correspond to innovations in the equations of the response variables ordered by Mdl.SeriesNames.
Tip
A good practice is to run simsmooth multiple times with different parameter starting values. Verify that the estimates from each run converge to similar values.
Data Types: double
Output Arguments
Simulated VAR model coefficients, returned as a (PriorMdl.NumSeries*)-by-kNumDraws numeric matrix, where k = PriorMdl.NumSeries*PriorMdl.P + PriorMdl.IncludeIntercept + PriorMdl.IncludeTrend + PriorMdl.NumPredictors
Each column is a successive draw (vector of coefficients) from the posterior distribution.
For draw jCoeffDraws(1: corresponds to all coefficients in the equation of response variable k,j)PriorMdl.SeriesNames(1), Coeff(( corresponds to all coefficients in the equation of response variable k + 1):(2*k),j)PriorMdl.SeriesNames(2), and so on. For a set of indices corresponding to an equation:
Elements
1throughPriorMdl.NumSeriescorrespond to the lag 1 AR coefficients of the response variables ordered byPriorMdl.SeriesNames.Elements
PriorMdl.NumSeries + 1through2*PriorMdl.NumSeriescorrespond to the lag 2 AR coefficients of the response variables ordered byPriorMdl.SeriesNames.In general, elements
(throughq– 1)*PriorMdl.NumSeries + 1q*PriorMdl.NumSeriesqPriorMdl.SeriesNames.If
PriorMdl.IncludeConstantistrue, elementPriorMdl.NumSeries*PriorMdl.P + 1is the model constant.If
Mdl.IncludeTrendistrue, elementPriorMdl.NumSeries*PriorMdl.P + 2is the linear time trend coefficient.If
PriorMdl.NumPredictors> 0, elementsPriorMdl.NumSeries*PriorMdl.P + 3throughk
This figure shows the structure of CoeffDraws(:, for a 2-D VAR(3) model that contains a constant vector and four exogenous predictors.j)
where
ϕq,jk is element (j,k) of the lag q AR coefficient matrix.
cj is the model constant in the equation of response variable j.
Bju is the regression coefficient of exogenous variable u in the equation of response variable j.
Simulated innovations covariance matrices, returned as a PriorMdl.NumSeries-by-PriorMdl.NumSeries-by-NumDraws array of positive definite numeric matrices.
Each page is a successive draw (covariance) from the posterior distribution. Rows and columns correspond to innovations in the equations of the response variables ordered by PriorMdl.SeriesNames.
If PriorMdl is a normalbvarm object, all covariances in SigmaDraws are equal to PriorMdl.Covariance.
Imputations for missing response data, returned as a numNaNs-by-NumDraws numeric matrix, where numNaNs = sum(isNaN(Y)), the number of NaNs in the response data.
Each column is a successive draw (vector of response imputations) from the posterior predictive distribution.
Each row corresponds to a NaN in Y. simsmooth determines the order of the rows by using a column-wise search. For example, suppose Y is the following matrix.
Y = [ 1 NaN;... NaN 2 ;... NaN 5 ;... 7 8];
NaNDraws is a 3-by-NumDraws matrix. For draw jNaNDraws(1,j) contains the imputed value of the response variable PriorMdl.SeriesNames(1) at time 2, NaNDraws(2,j) contains the imputed value of the response variable PriorMdl.SeriesNames(1) at time 3, and NaNDraws(3,j) contains the imputed value of the response variable PriorMdl.SeriesNames(2) at time 1.Augmented response data, returned as a numobs-by-PriorMdl.NumSeries numeric matrix. YMean is equal to the non-presample portion of the response data Y, but simsmooth replaces each NaN with the corresponding mean of the posterior predictive distribution (YMean contains zero missing values).
Standard deviations of the posterior predictive distribution of the imputed responses, returned as a numobs-by-PriorMdl.NumSeries numeric matrix. The dimensions of YStd and YMean correspond.
Missing values in the response data Y, which correspond to imputed values in YMean, have a nonzero standard deviation. Standard deviations corresponding to nonmissing response data are 0.
More About
A Bayesian VAR model treats all coefficients and the innovations covariance matrix as random variables in the m-dimensional, stationary VARX(p) model. The model has one of the three forms described in this table.
| Model | Equation |
|---|---|
| Reduced-form VAR(p) in difference-equation notation |
|
| Multivariate regression |
|
| Matrix regression |
|
For each time t = 1,...,T:
yt is the m-dimensional observed response vector, where m =
numseries.Φ1,…,Φp are the m-by-m AR coefficient matrices of lags 1 through p, where p =
numlags.c is the m-by-1 vector of model constants if
IncludeConstantistrue.δ is the m-by-1 vector of linear time trend coefficients if
IncludeTrendistrue.Β is the m-by-r matrix of regression coefficients of the r-by-1 vector of observed exogenous predictors xt, where r =
NumPredictors. All predictor variables appear in each equation.which is a 1-by-(mp + r + 2) vector, and Zt is the m-by-m(mp + r + 2) block diagonal matrix
where 0z is a 1-by-(mp + r + 2) vector of zeros.
, which is an (mp + r + 2)-by-m random matrix of the coefficients, and the m(mp + r + 2)-by-1 vector λ = vec(Λ).
εt is an m-by-1 vector of random, serially uncorrelated, multivariate normal innovations with the zero vector for the mean and the m-by-m matrix Σ for the covariance. This assumption implies that the data likelihood is
where f is the m-dimensional multivariate normal density with mean ztΛ and covariance Σ, evaluated at yt.
Before considering the data, you impose a joint prior distribution assumption on (Λ,Σ), which is governed by the distribution π(Λ,Σ). In a Bayesian analysis, the distribution of the parameters is updated with information about the parameters obtained from the data likelihood. The result is the joint posterior distribution π(Λ,Σ|Y,X,Y0), where:
Y is a T-by-m matrix containing the entire response series {yt}, t = 1,…,T.
X is a T-by-m matrix containing the entire exogenous series {xt}, t = 1,…,T.
Y0 is a p-by-m matrix of presample data used to initialize the VAR model for estimation.
A posterior predictive distribution of a posterior Bayesian VAR(p) model π(Yf|Y,X) is the distribution of the next τ future response variables after the final observation in the estimation sample Yf = [yT+1, yT+2,…,yT+τ] given the following, marginalized over Λ and Σ:
Presample and estimation sample response data Y
Coefficients Λ
Innovations covariance matrix Σ
Estimation and future sample exogenous data X
Symbolically,
The Gibbs sampler with Bayesian data augmentation is a Markov Chain Monte Carlo sampling method that draws from the posterior distribution of the parameters and unobserved response data given the observed data.
Consider these sets of indices:
I = {(i,j) | i = 1,…,m +τ, j = 1,…,m +τ}, the universe containing all index pairs (i,j) of non-presample data and the forecast horizon. Y(I) represents the entire non-presample response data including any placeholders (
NaNvalues) for missing observations and unobserved values in the forecast horizon.U = {(i,j) ∈ I | Y(i,j) is missing or unobserved}, the set of index pairs corresponding to missing or unobserved response data. Y(U) is a set of placeholders, and Y(Uc) is the set of observed data.
simsmooth simulates from the posterior distribution of the missing response data, coefficients, and innovations covariance matrix by following this Gibbs sampler.
Create an observation-error-free state-space model by applying the specified VAR(p) structure to the state equations. Apply the initial parameter values Λ(0) and Σ(0) (
Coeff0andSigma0). The resulting model is the conditional posterior predictive distribution π(Y(U)|Λ(0),Σ(0),Y(Uc),X).During iteration j:
Simulate missing response data Y(U)(j) from π(Y(U) | Λ(j-1),Σ(j-1),Y(Uc),X). To accomplish this action,
simsmoothuses the state-space model simulation smoother (see thesimsmoothfunction of thessmmodel object).simsmoothstores Y(U)(j) in the outputNaNDraws.Compose the augmented data set Y(I)(j) = Y(U)(j) ∪ Y(Uc).
Draw coefficients Λ(j) and an innovations covariance matrix Σ(j) from the conditional posterior Bayesian VAR model with augmented data π(Λ,Σ | Y(I)(j),X).
simsmoothstores Λ(j) and Σ(j) in the outputsCoeffDrawsandSigmaDraws, respectively.
The mean and standard deviation of the posterior predictive distribution π(Y(U) | Λ,Σ,Y(Uc),X) is the mean and standard deviation of the series of draws {Y(U)(j)}.
simsmoothstores the statistics in the outputsYMeanandYStd.
After removing the burn-in period (Burnin) and thinning the sample (Thin), simsmooth stores the remaining set of draws and computes posterior statistics from it.
Tips
Monte Carlo simulation is subject to variation. If
simsmoothuses Monte Carlo simulation, then estimates and inferences might vary when you callsimsmoothmultiple times under seemingly equivalent conditions. To reproduce estimation results, set a random number seed by usingrngbefore callingsimsmooth.
Algorithms
This figure shows how
simsmoothreduces the sample by using the values ofNumDraws,Thin, andBurnIn. Rectangles represent successive draws from the distribution.simsmoothremoves the white rectangles from the sample. The remainingNumDrawsblack rectangles compose the sample.
simsmoothdoes not return default starting values that it generates.
References
[1] Litterman, Robert B. "Forecasting with Bayesian Vector Autoregressions: Five Years of Experience." Journal of Business and Economic Statistics 4, no. 1 (January 1986): 25–38. https://doi.org/10.2307/1391384.
Version History
Introduced in R2020a
See Also
Objects
Functions
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Web サイトの選択
Web サイトを選択すると、翻訳されたコンテンツにアクセスし、地域のイベントやサービスを確認できます。現在の位置情報に基づき、次のサイトの選択を推奨します:
また、以下のリストから Web サイトを選択することもできます。
最適なサイトパフォーマンスの取得方法
中国のサイト (中国語または英語) を選択することで、最適なサイトパフォーマンスが得られます。その他の国の MathWorks のサイトは、お客様の地域からのアクセスが最適化されていません。
南北アメリカ
- América Latina (Español)
- Canada (English)
- United States (English)
ヨーロッパ
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)