LMS Filter
Libraries:
DSP HDL Toolbox /
Filtering
Description
The LMS Filter block estimates the filter weights and minimizes the error between a desired signal and an observed signal using the mean square error (MSE) criteria. The block adapts its weights until the error between the data and the desired data is minimal. The block accepts scalar and vector inputs of type real and complex.
You can use this block for various applications, such as noise cancellation, system identification, and inverse system modeling. The block provides an architecture suitable for HDL code generation and hardware deployment.
Note
You can also generate HDL code for this hardware-optimized algorithm, without creating a Simulink® model, by using the DSP HDL IP Designer app. The app provides the same interface and configuration options as the Simulink block.
Examples
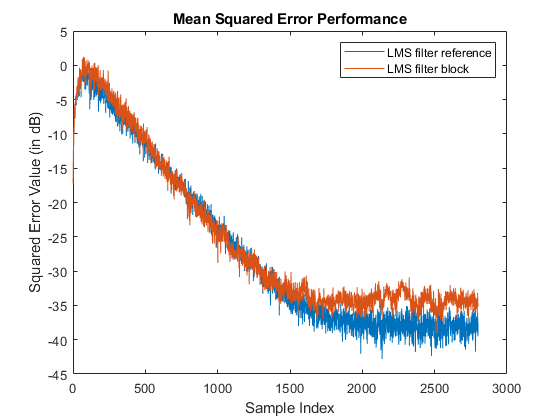
Calculate Mean Square Error Performance Using LMS Filter
How use the LMS Filter block to calculate the mean square error performance in additive white Gaussian noise (AWGN). The block supports scalar and vector inputs of type real or complex. You can generate the HDL code from the LMSFilter subsystem in this Simulink® model.
Ports
Input
Input data, specified as a scalar or column vector of real or complex values. The input vector size must be in the range [2, 64] and it must be less than the filter length. The block can only support input word lengths of up to 32 bits.
Use double and single data types for
simulation, but not for HDL code generation. For HDL code generation, the input date
type must be signed fixed point.
Data Types: single | double | fixed point
Complex Number Support: Yes
Desired input data, specified as a scalar or column vector of real or complex values. The input vector size must be in the range [2, 64] and it must be less than filter length. The desired port must have the same data type, complexity, and dimensions as the input data port.
Data Types: single | double | fixed point
Complex Number Support: Yes
Control signal that indicates if the input data is valid. When
valid is 1 (true), the
block captures the values from the input ports data and
desired. When valid is
0 (false), the block ignores the values from
the input ports data and desired.
Data Types: Boolean
Specify the step size to control convergence and stability of the filter. The recommended step size must be less than 1/(2 x Input power x Filter length).
You can use double and single data types for
simulation, but not for HDL code generation. For HDL code generation, the input date
type must be unsigned fixed point.
Dependencies
To enable this port, on the Main tab, set the
Step-size source parameter to Input
port.
Data Types: double | single | fixed point
When adapt is 1 (true)
and input valid is 1
(true), the block adapts to the new filter weights for every input
valid. When the adapt is
0 (false) and the input
valid is 1 (true) or
0 (false), the block remains at its previous
filter weights.
Dependencies
To enable this port, on the Main tab, select the Enable adapt input port parameter.
Data Types: Boolean
Control signal that clears internal states. When reset is
1 (true), the block stops the current
calculation, clears internal states, and sets to the initial values of filter weights
specified on the block mask. When the reset is
0 (false) and the input
valid is 1 (true), the
block captures data for processing.
For more reset considerations, see the Reset Signal section on the Hardware Control Signals page.
Dependencies
To enable this port, on the Control Ports tab, select the Enable reset input port parameter.
Data Types: Boolean
Output
Filtered output data, returned as a scalar or column vector of real or complex values. The dimensions of the output match the dimensions of the input.
When the input data is a floating-point type, the output data inherits the data type of the input data. When the input data is a fixed-point type, the output data is a fixed point with word length and fractional length incremented by 1.
Data Types: single | double | fixed point
Complex Number Support: Yes
Control signal that indicates if the data from the output
data port is valid. When valid is
1 (true), the block returns valid data from
the output data port. When valid is
0 (false), the values from the output
data port are not valid.
Data Types: Boolean
Outputs the result of subtracting the filtered output signal from the desired
signal when the output valid is 1
(true).
If the input data and desired is a scalar or a column vector, the error signal has the same dimension and complexity as the input data. When the input data is a floating-point type, the output data inherits the data type of the input data. When the input data is a fixed-point type, the output data is fixed point with word length incremented by 2 and fractional length incremented by 1.
Dependencies
To enable this port, on the Main tab, select the Enable filter error output port parameter.
Data Types: Boolean
For each iteration, the block outputs the current updated filter weights from this
port when the output valid is 1
(true).
For floating-point inputs, the weights data type must match the input type. For fixed-point signals, the input must match the data type set to the Weights parameter.
Dependencies
To enable this port, on the Main tab, select the Enable filter weights output port parameter.
Data Types: Boolean
Parameters
Main
Specify the length of the LMS filter as a positive integer less than or equal to 2048.
Select whether the block specifies the step size through property or input port.
Property— Specify step size by using the Step size (mu) parameter.Input port— Specify step size by using the stepSize port.
Specify the step size as a positive scalar numeric value. The recommended step size must be less than 1/(2 x Input power x Filter length).
Dependencies
To enable this parameter, set the Step-size source
parameter to Property.
Enter the initial filter weights as a scalar or row vector of size equal to filter length.
When you specify a scalar value, the block considers it as a row vector equivalent to the specified scalar value.
Select this parameter to enable the adapt input port.
Select this parameter to enable the weights output port.
For each iteration, the block outputs the current updated filter weights from this port.
Select this parameter to enable the error output port.
Data Types
Rounding mode for type-casting the output to the data type specified by the Output parameter. When the input data type is floating point, the block ignores this parameter. For more details, see Rounding Modes.
Overflow handling for type-casting the output to the data type specified by the Output parameter. When the input data type is floating point, the block ignores this parameter. For more details, see Overflow Handling.
Specify the step size data type.
Dependencies
To enable this parameter, set the Step-size source
parameter to Property.
Specify the data type for the filter weights.
Specify the step size error product.
Control Ports
Select this check box to enable the reset input port. The reset signal implements a local synchronous reset of the data path registers.
For more reset considerations, see the Reset Signal section on the Hardware Control Signals page.
Select this check box to connect the generated HDL global reset signal to the data path registers. This parameter does not change the appearance of the block or modify simulation behavior in Simulink. When you clear this check box, the generated HDL global reset clears only the control path registers. The generated HDL global reset can be synchronous or asynchronous depending on the HDL Code Generation > Global Settings > Reset type parameter in the model Configuration Parameters.
For more reset considerations, see the Reset Signal section on the Hardware Control Signals page.
Algorithms
The following figure shows the high-level architecture block diagram of the LMS Filter block for a scalar input. An observed signal is provided as input to the Input Memory block and also to the Transpose Filter block, which is configured with a Discrete FIR Filter block. The output of the Transpose Filter block is subtracted from the Desired input signal to output the Filter Error signal. The Filter Error signal is multiplied with the Step-Size input signal and the resulted step-error product is converted to the required data type. The step-error product is multiplied with the corresponding tap delay line conjugate from the Input Memory block. In the Integrator block, the multiplied output is added to the previous weight, Unit Delay, to output new filter weights. These filter weights are routed back to the Transpose Filter block for the next weight updates.

The following figure shows the high-level architecture block diagram of the LMS Filter block for vector input. The vector architecture is almost similar to the scalar architecture. In the vector architecture, step-error product vectors are multiplied with the corresponding tap delay line conjugates from the Input Memory block and then summed up in the Summation block. In the Integrator block, the summed output is added to the previous weight vector Unit Delay to output new filter weights. These filter weights are routed back to the Transpose Filter block for the next weight updates.

For hardware implementation, all these operations are pipelined, which takes around D number of delays to update the filter weights, where D is the latency of the block.
The latency of the block varies with the input size and complexity.
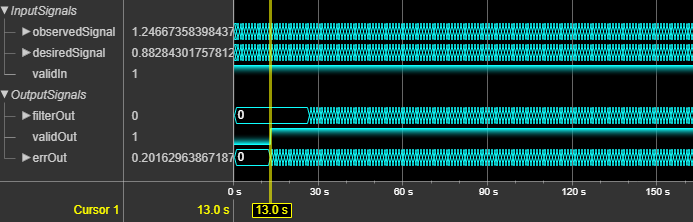
This figure shows the output of the block for a real scalar input when you set the
Filter length parameter to 64 and all
other parameters to their default values. The latency of the block is 13 clock
cycles.
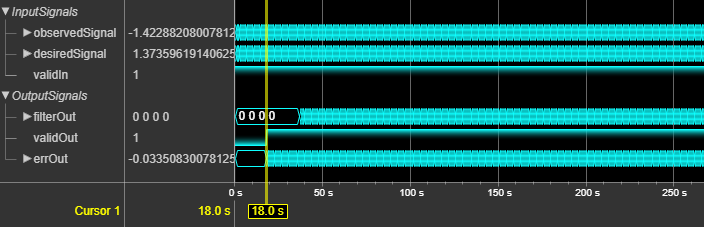
This figure shows the output of the block for a 4-by-1 real vector input when you set
the Filter length parameter to 64 and all
other parameters to their default values. The latency of the block is 18 clock
cycles.
The performance of the synthesized HDL code varies with your target and synthesis options. These resource and performance data are the place-and-route results from the generated HDL targeted to an AMD® Zynq® UltraScale+™ MPSoC evaluation board. The two examples in the following tables use this common configuration.
Filter length — 64
16-bit real input data
Step size (mu) — 0.006
Initial value of filter weights — 0
For a scalar input, the design achieves a clock frequency of 523.01 MHz. The design uses these resources.
| Resource | Number Used |
|---|---|
| LUT | 8402 |
| FFS | 18819 |
AMD LogiCORE® DSP48 | 129 |
For a 4-by-1 vector input, the design achieves a clock frequency of 512.82 MHz. The design uses these resources.
| Resource | Number Used |
|---|---|
| LUT | 27712 |
| FFS | 30322 |
AMD LogiCORE DSP48 | 516 |
Using a vector input can increase the throughput, however, doing so also increases the number of hardware resources that the block uses.
References
[1] Hayes, M.H. Statistical Digital Signal Processing and Modeling. New York: John Wiley & Sons, 1996.
Extended Capabilities
This block supports C/C++ code generation for Simulink accelerator and rapid accelerator modes and for DPI component generation.
HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic.
This block has one default HDL architecture.
| ConstrainedOutputPipeline | Number of registers to place at
the outputs by moving existing delays within your design. Distributed
pipelining does not redistribute these registers. The default is
|
| InputPipeline | Number of input pipeline stages
to insert in the generated code. Distributed pipelining and constrained
output pipelining can move these registers. The default is
|
| OutputPipeline | Number of output pipeline stages
to insert in the generated code. Distributed pipelining and constrained
output pipelining can move these registers. The default is
|
Version History
Introduced in R2023a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Web サイトの選択
Web サイトを選択すると、翻訳されたコンテンツにアクセスし、地域のイベントやサービスを確認できます。現在の位置情報に基づき、次のサイトの選択を推奨します:
また、以下のリストから Web サイトを選択することもできます。
最適なサイトパフォーマンスの取得方法
中国のサイト (中国語または英語) を選択することで、最適なサイトパフォーマンスが得られます。その他の国の MathWorks のサイトは、お客様の地域からのアクセスが最適化されていません。
南北アメリカ
- América Latina (Español)
- Canada (English)
- United States (English)
ヨーロッパ
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)