このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

ズーム FFT

この例では、ズーム FFT を紹介します。ズーム FFT は、スペクトルの高分解能な解析に使用される信号処理手法です。DSP System Toolbox™ は、MATLAB® では dsp.ZoomFFT System object™ を介して、Simulink® では DSP System Toolbox ライブラリの Zoom FFT ブロックを介してこの機能を提供します。

標準 DFT/FFT の制限

デジタル信号の長さによって、そのスペクトル分解能が決まります。次の例はこれを示しています。まず、2 つの正弦波の和である信号を作成します。

L   = 32;       % Frame size
Fs  = 128;      % Sample rate
res = Fs/L;     % Frequency resolution
f1  = 40;       % First sine wave frequency
f2  = f1 + res; % Second sine wave frequency
 
sn1 = dsp.SineWave(Frequency=f1, SampleRate=Fs, SamplesPerFrame=L);
sn2 = dsp.SineWave(Frequency=f2, SampleRate=Fs, SamplesPerFrame=L, Amplitude=2);

x = sn1() + sn2();

x の FFT を計算し、FFT の振幅をプロットしてみます。FFT の隣接するサンプルにこの 2 つの正弦波が位置しています。これは、$\frac{{\mathrm{F}}_{\mathit{s}}}{\mathit{L}}$ よりも近い範囲の周波数どうしは区別できないということを意味します。

X = fft(x);
scopeFFT = dsp.ArrayPlot(SampleIncrement=Fs/L, ...
    XOffset=-Fs/2, ...
    XLabel="Frequency (Hz)", ...
    YLabel="Magnitude", ...
    Title="Two-sided spectrum", ...
    YLimits=[-0.1 1.1]);
scopeFFT(abs(fftshift(X))/L);

ズーム FFT

ナイキスト区間のサブ帯域のみを対象とする応用事例があるとします。ズーム FFT の背景にある概念は、短い信号の小さい FFT を計算して元の信号のフル サイズの FFT から得られる分解能と同じ分解能を得ることです。短い信号は元の信号を間引きしたものです。はるかに短い FFT の計算から同じ分解能が得られれば負荷の軽減になります。間引き係数を D とすると、新しいサンプル レートは ${\mathit{F}}_{\mathrm{sd}}=\frac{{\mathrm{F}}_{\mathit{s}}}{\mathit{D}}$、新しいフレーム サイズ (および FFT 長) は ${\mathit{L}}_{\mathit{d}}=\frac{\mathit{L}}{\mathit{D}}$ となり、間引き信号の分解能は $\frac{{\mathit{F}}_{\mathrm{sd}}}{{\mathit{L}}_{\mathit{d}}}=\frac{{\mathrm{F}}_{\mathit{s}}}{\mathit{L}}$ となります。

混合器手法

混合器手法は、一般的なズーム FFT の手法です。

[16 Hz, 48 Hz] の帯域幅間隔のみを対象にすると仮定し、その間隔の中心周波数を計算します。

BWOfInterest = 48 - 16;
Fc           = (16 + 48)/2; % Center frequency of bandwidth of interest

前のセクションの例のサンプル レートを使用して、達成可能な間引き係数を計算します。

BWFactor = floor(Fs/BWOfInterest)

BWFactor = 4

混合器手法では、最初に混合器を使用して対象の帯域を DC まで下にシフトし、次にローパス フィルター処理と係数 BWFactor による間引きを行います。

関数designMultirateFIRを使用して、間引きフィルターの係数を設計します。dsp.FIRDecimator System object は、効率的なポリフェーズ FIR 間引き構造を使用してローパス演算とダウンサンプリング演算を実装します。

B = designMultirateFIR(1, BWFactor);
D = dsp.FIRDecimator(BWFactor, B);

信号を混合して DC まで下げ、FIR 間引きによってフィルター処理します。

% Run several input frames to eliminate the FIR transient response
for k = 1:10
    % Grab a frame of the input signal
    x = sn1()+sn2();

    % Downmix to DC
    indVect = (0:numel(x)-1).' + (k-1) * size(x,1);
    y = x .* exp(-2*pi*indVect*Fc*1j/Fs);

    % Filter through FIR decimator
    xd = D(y);    
end

フィルター処理された信号の FFT を計算します。同じ分解能を維持するために、混合器手法の FFT 長は、通常の FFT 変換の FFT 長と比較して、BWFactor つまり間引きの長さだけ減少します。

Xd  = fft(xd);
Ld  = L/BWFactor;
Fsd = Fs/BWFactor;

scopeMixing = dsp.ArrayPlot(SampleIncrement=Fs/L, ...
    XOffset=Fsd/2, ...
    XLabel="Frequency (Hz)", ...
    YLabel="Magnitude", ...
    Title="Zoom FFT Spectrum: Mixer Approach", ...
    YLimits=[-0.1 1.1]);

scopeMixing(abs(fftshift(Xd))/Ld);

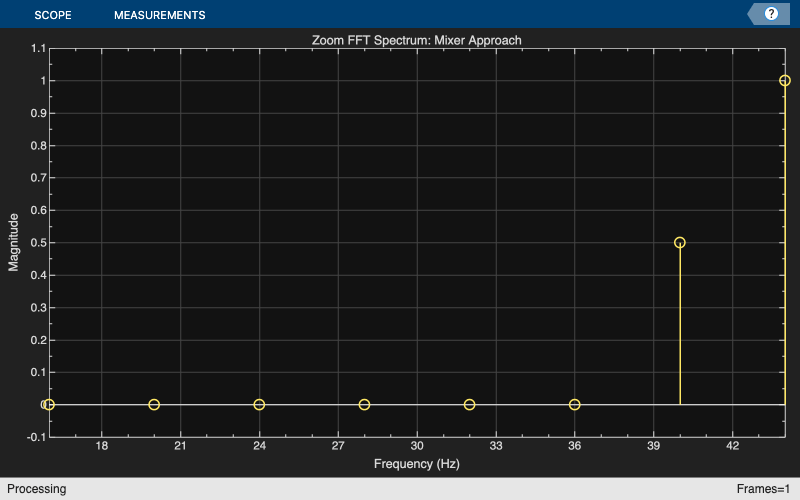
複素数値の混合器は各高レート サンプルに対して乗算演算を追加しますが、これは効率的ではありません。次の節では、より効率的な代替手段であるズーム FFT アプローチについて説明します。

バンドパスのサンプリング

代替のズーム FFT 手法はバンドパス フィルター処理の既知の結果を活用します (アンダーサンプリングと呼ばれる場合もあります)。サンプル レート ${\mathit{F}}_{\mathit{s}}$ の信号の帯域 $\left[{\mathit{F}}_1,{\mathit{F}}_2\right]$ を考えるものとします。中心が ${\mathit{F}}_{\mathit{c}}=\frac{{\mathit{F}}_1+{\mathit{F}}_2}{2}$ で帯域幅が $\mathrm{BW}={\mathit{F}}_2-{\mathit{F}}_1$ の複素 (片側) バンドパス フィルターに信号を通過させ、$D=\lfloor \frac{{\mathit{F}}_{\mathit{s}}}{\mathrm{BW}}\rfloor$ 分の 1 にダウンサンプリングすると、目的の帯域はベースバンドまで下がります。

一般的に ${\mathit{F}}_{\mathit{c}}$ が $k\frac{{\mathit{F}}_{\mathit{s}}}{\mathit{D}}$ (k は整数) の形式で表現できない場合、シフトした間引きスペクトルの中心は DC になりません。実際には中心周波数 Fc は次のように変換されます [2]。

$${\mathit{F}}_{\mathit{d}}={\mathit{F}}_{\mathit{c}}-\frac{{\mathit{F}}_{\mathit{s}}}{\mathit{D}}\lfloor \frac{\mathit{D}\cdot {\mathit{F}}_{\mathit{c}}+{\mathit{F}}_{\mathit{s}}/2}{{\mathit{F}}_{\mathit{s}}}\rfloor$$

この場合、混合器を使用して (間引き信号の低サンプル レートで実行) 目的の帯域の中心をゼロ ヘルツにできます。

前のセクションの例を使用して、設計されたローパス フィルターの係数を変調することにより、複素バンドパス フィルターの係数を取得します。

N   = length(D.Numerator);
Bbp = B .*exp(1j*(Fc / Fs)*2*pi*(0:N-1));
Dbp = dsp.FIRDecimator(BWFactor, Bbp);

フィルター処理と FFT 演算を実行します。

for k = 1:10
    % Run a few times to eliminate transient in filter
    x = sn1()+sn2();
    xd = Dbp(x);    
end
Xd = fft(xd);
scopeBandpassSampling = dsp.ArrayPlot(SampleIncrement=Fs/L, ...
    XOffset=Fsd/2, ...
    XLabel="Frequency (Hz)", ...
    YLabel="Magnitude", ...
    Title="Zoom FFT Spectrum: Bandpass Sampling Approach", ...
    YLimits=[-0.1 1.1]);
scopeBandpassSampling(abs(fftshift(Xd))/Ld);

マルチレート多段バンドパス フィルター

前のセクションの FIR 間引きは単一ステージ マルチレート フィルターです。代わりに多段設計を使用してフィルターの計算量を削減できます (実際に、これは dsp.ZoomFFT System object で利用されているアプローチです)。詳細については、Multistage Rate Conversionを参照してください。

入力サンプル レートが 48 kHz で対象の帯域幅が区間 [1500,2500] Hz である次の例について検討します。この場合、実現可能な間引き係数は $\lfloor \frac{48000}{1000}\rfloor =48$ です。

最初に単一ステージの間引きを設計します。

Fs       = 48e3;
Fc       = 2000; % Bandpass filter center frequency
BW       = 1e3;  % Bandwidth of interest
Ast      = 80;   % Stopband attenuation
P        = 12;   % Polyphase length
BWFactor = floor(Fs/BW);
B        = designMultirateFIR(1,BWFactor,P,Ast);
N        = length(B);
Bbp      = B .*exp(1j*(Fc / Fs)*2*pi*(0:N-1));
D_single_stage = dsp.FIRDecimator(BWFactor, Bbp);

次に多段設計を使用して同じ間引きを実装しますが、単一ステージの場合と同じ阻止帯域の減衰量と遷移帯域幅を維持します。遷移幅の計算方法の詳細については、kaiserordを参照してください。

tw = (Ast - 7.95) / ( N * 2.285);
D_multi_stage = designMultistageDecimator(BWFactor, Fs, tw*Fs/(2*pi), Ast);
fprintf("Number of filter stages: %d\n", getNumStages(D_multi_stage) );

Number of filter stages: 5

for ns=1:D_multi_stage.getNumStages
    stgn = D_multi_stage.("Stage" + ns);
    fprintf("Stage %i: Decimation factor = %d , FIR length = %d\n",...
            ns, stgn.DecimationFactor,...
            length(stgn.Numerator));
end

Stage 1: Decimation factor = 2 , FIR length = 7
Stage 2: Decimation factor = 2 , FIR length = 7
Stage 3: Decimation factor = 2 , FIR length = 11
Stage 4: Decimation factor = 2 , FIR length = 15
Stage 5: Decimation factor = 3 , FIR length = 75

このフィルターは 5 段のマルチレート ローパス フィルターです。これを累積間引き係数を考慮に入れながら各段の係数について周波数シフトを実行することによってバンドパス フィルターに変換します。

Mn = 1; % Cumulative decimation factor entring stage n
for ns=1:D_multi_stage.getNumStages
    stgn = D_multi_stage.("Stage" + ns);
    num  = stgn.Numerator;
    N    = length(num);
    num  = num .*exp(1j*(Fc * Mn/ Fs)*2*pi*(0:N-1));
    stgn.Numerator = num;
    Mn   = Mn*stgn.DecimationFactor;
end

単一ステージ フィルターのコストを計算します。

cost(D_single_stage)

ans = struct with fields:
                  NumCoefficients: 1129
                        NumStates: 1104
    MultiplicationsPerInputSample: 23.5208
          AdditionsPerInputSample: 23.5000

多段フィルターのコストを計算します。このフィルターでは計算効率が大幅に向上します。

cost(D_multi_stage)

ans = struct with fields:
                  NumCoefficients: 77
                        NumStates: 108
    MultiplicationsPerInputSample: 6.2500
          AdditionsPerInputSample: 5.2917

次に、2 つのフィルターの周波数応答を比較し、2 つのフィルターの通過帯域特性が同じであることを確認します。阻止帯域の相違はごくわずかです。

vis = fvtool(D_single_stage,D_multi_stage,DesignMask="off",legend="on");
legend(vis,"Single-stage","Multistage")

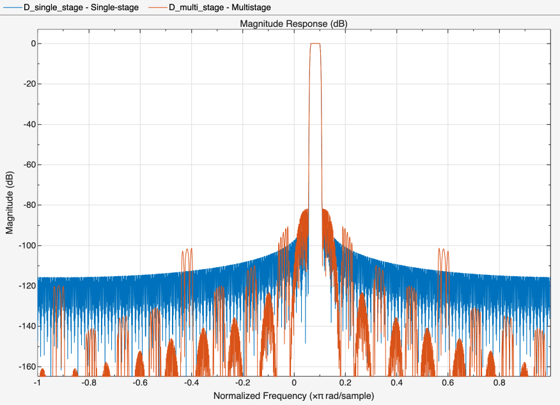
最後に、多段フィルターを使用してズーム FFT を実行します。

fftlen = 32;
L      = BWFactor * fftlen;
tones  = [1625 2000 2125]; % sine wave tones
sn     = dsp.SineWave(SampleRate=Fs, Frequency=tones, SamplesPerFrame=L);
Fsd    = Fs / BWFactor;
% Frequency points at which FFT is computed
F      = Fc + Fsd/fftlen*(0:fftlen-1)-Fsd/2;

% Step through the bandpass-decimator 
for k=1:100
    x = sum(sn(),2) +  1e-2 * randn(L,1);
    y = D_multi_stage(x);
end 

% Plot the spectral output
scopeZoomFFT = dsp.ArrayPlot(XDataMode="Custom",...
                   CustomXData=F,...
                   YLabel="Magnitude",...
                   XLabel="Frequency (Hz)",...
                   YLimits=[0 1],...
                   Title=sprintf ("Zoom FFT: Resolution = %f Hz",(Fs/BWFactor)/fftlen));

z = fft(y,fftlen,1);
z = fftshift(z);

scopeZoomFFT( abs(z)/fftlen )
release(scopeZoomFFT)

dsp.ZoomFFT の使用

dsp.ZoomFFT System object は、前のセクションで説明したマルチレート多段バンドパス フィルターに基づいてズーム FFT を実装します。目的の中心周波数と間引き係数を指定すると、dsp.ZoomFFT によってフィルターが設計され、入力信号に適用されます。

dsp.ZoomFFT を使用して、前のセクションの信号の正弦波トーンにズームインします。

zfft = dsp.ZoomFFT(BWFactor,Fc,Fs);
for k=1:100
    x = sum(sn(),2) + 1e-2 * randn(L,1);
    z = zfft(x);
end 

z = fftshift(z);
scopeZoomFFT( abs(z)/fftlen)

release(scopeZoomFFT)

参照

[1] Multirate Signal Processing - Harris (Prentice Hall).

[2] Computing Translated Frequencies in digitizing and Downsampling Analog Bandpass - Lyons (https://www.dsprelated.com/showarticle/523.php)

参考

dsp.ZoomFFT | Zoom FFT | designMultirateFIR

関連するトピック

• Analyze a Subband of Input Frequencies Using Zoom FFT
• Multistage Rate Conversion