MATLAB でのパワースペクトルの推定

時間領域信号のパワースペクトル (PS) とは、有限長のデータをベースに、信号内に含まれているパワーを周波数上に分布したものです。信号の周波数領域表現は、時間領域表現よりも解析が容易である場合が多くあります。ノイズキャンセリングやシステム同定といった多くの信号処理アプリケーションは、周波数に特化した信号修正に基づいています。パワースペクトル推定の目的は、時間サンプルのシーケンスから信号のパワースペクトルを推定することです。信号に関する既知の情報に応じて、パラメトリックアプローチまたはノンパラメトリックアプローチが推定法として使用され、時間領域解析または周波数領域解析に基づいて推定が行われます。たとえば、一般的なパラメトリック手法では、観測値を自己回帰モデルに適合させます。一般的なノンパラメトリック手法はピリオドグラムです。パワースペクトルは、ウェルチ法やフィルターバンク法といったフーリエ変換法を使用して推定されます。比較的長さが短い信号の場合、フィルターバンクアプローチによって、より高い分解能とより正確なノイズフロアをもつスペクトル推定が生成され、ウェルチ法よりも正確なピークを示します。スペクトル漏れは低いかまったくありません。こうした利点には、計算量の増加と追跡の低速化という代償が伴います。これらの方法の詳細については、Spectral Analysisを参照してください。最大エントロピー法のようなその他の手法を使用することもできます。

MATLAB^® では、dsp.SpectrumAnalyzer System object™ を使用して動的な信号のリアルタイムスペクトル解析を実行することができます。オブジェクト関数 isNewDataReady および getSpectrumData を使用して、スペクトルデータをスペクトルアナライザーに表示し、そのデータをワークスペース変数に格納することができます。あるいは、dsp.SpectrumEstimator System object を使用した後で dsp.ArrayPlot オブジェクトを使用することでスペクトルデータを表示することもできます。dsp.SpectrumEstimator オブジェクトの出力はスペクトルデータです。このデータを取得して、その後の処理で使用できます。

dsp.SpectrumAnalyzer を使用したパワースペクトルの推定

スクリプトを開く

信号のパワースペクトルを表示するには、dsp.SpectrumAnalyzer System object™ を使用できます。入力信号のダイナミクスを変更して、その変更が信号のパワースペクトルに与える影響をリアルタイムに確認することができます。

初期化

正弦波ソースを初期化して正弦波とスペクトルアナライザーを生成し、信号のパワースペクトルを表示します。入力正弦波は 2 つの周波数 (1 つは 1000 Hz、もう 1 つは 5000 Hz) をもちます。2 つの dsp.SineWave オブジェクトを作成します。1 つは 1000 Hz 正弦波を生成し、もう 1 つは 5000 Hz 正弦波を生成するオブジェクトです。

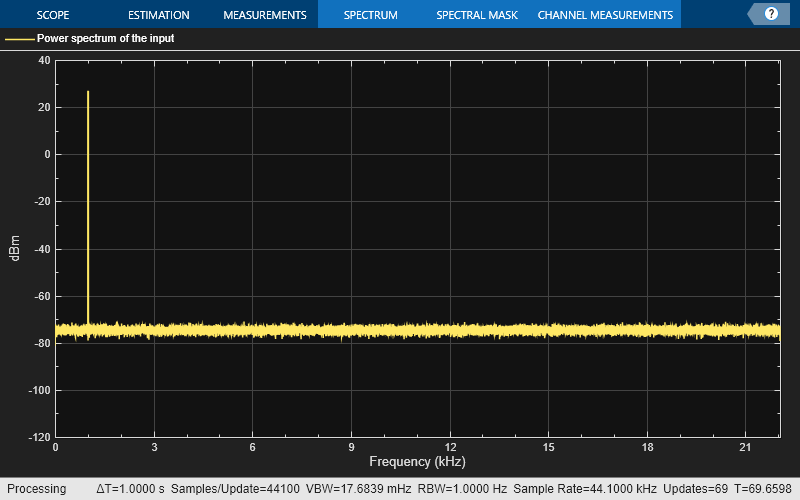
Fs = 44100;
Sineobject1 = dsp.SineWave('SamplesPerFrame',1024,'PhaseOffset',10,...
    'SampleRate',Fs,'Frequency',1000);
Sineobject2 = dsp.SineWave('SamplesPerFrame',1024,...
    'SampleRate',Fs,'Frequency',5000);
SA = dsp.SpectrumAnalyzer('SampleRate',Fs,'Method','Filter bank',...
    'SpectrumType','Power','PlotAsTwoSidedSpectrum',false,...
    'ChannelNames',{'Power spectrum of the input'},'YLimits',[-120 40],'ShowLegend',true);

スペクトルアナライザーはフィルターバンクアプローチを使用して、信号のパワースペクトルを計算します。

推定

ストリーミングを行い、信号のパワースペクトルを推定します。for ループを作成して、5000 回の反復を実行します。各反復では、各正弦波の 1024 サンプル (1 フレーム) をストリーミングして、各フレームのパワースペクトルを計算します。入力信号を生成するために、2 つの正弦波を追加します。結果として得られる信号は 2 つの周波数 (1 つは 1000 Hz、もう 1 つは 5000 Hz) をもつ正弦波です。ゼロ平均、標準偏差 0.001 のガウスノイズを付加します。その後の処理で使用するスペクトルデータを取得するには、オブジェクト関数 isNewDataReady および getSpectrumData を使用します。変数 data には、スペクトルに関する追加の統計と共にスペクトルアナライザーに表示されるスペクトルデータが含まれています。

data = [];
for Iter = 1:7000
    Sinewave1 = Sineobject1();
    Sinewave2 = Sineobject2();
    Input = Sinewave1 + Sinewave2;
    NoisyInput = Input + 0.001*randn(1024,1);
    SA(NoisyInput);
     if SA.isNewDataReady
        data = [data;getSpectrumData(SA)];
     end
end
release(SA);

スペクトルアナライザーの出力では、2 つの明確なピーク (1 つは 1000 Hz、もう 1 つは 5000 Hz) を確認できます。

分解能帯域幅 (RBW) は、スペクトルアナライザーによって分解できる最小の周波数帯域幅です。既定では、dsp.SpectrumAnalyzer オブジェクトの RBWSource プロパティは Auto に設定されます。このモードでは、RBW は周波数スパンと 1024 の比率です。両側スペクトルでは、この値は $\frac{F_{s}}{1024}$ ですが、片側スペクトルでは $\frac{\frac{F_{s}}{2}}{1024}$ です。この例のスペクトルアナライザーは片側スペクトルを示しています。そのため、RBW は (44100/2)/1024、つまり 21.53 Hz です。

のこの値を使用すると、1 つのスペクトルの更新を計算するのに必要な入力サンプル数 $N_{samples}$ は、次の式で求められます。 $N_{samples} = \frac{F_{s}}{RBW}$

この例では、 $N_{samples}$ は 44100/21.53、つまり 2048 サンプルです。

'自動' モードで計算されたは、適切な周波数分解能を提供します。

表示される 2 つの周波数を区別するには、2 つの周波数間の距離が少なくとも RBW でなければなりません。この例では、2 つのピーク間の距離はより大きい 4000 Hz です。そのため、ピークをはっきりと確認することができます。2 番目の正弦波の周波数を 1015 Hz に変更します。2 つの周波数間の差はより小さくなっています。

release(Sineobject2);
Sineobject2.Frequency = 1015;
for Iter = 1:5000
    Sinewave1 = Sineobject1();
    Sinewave2 = Sineobject2();
    Input = Sinewave1 + Sinewave2;
    NoisyInput = Input + 0.001*randn(1024,1);
    SA(NoisyInput);
end
release(SA);

ピークは区別できません。

周波数分解能を向上させるには、を 1 Hz まで減らします。

SA.RBWSource = 'property';
SA.RBW = 1;
for Iter = 1:5000
    Sinewave1 = Sineobject1();
    Sinewave2 = Sineobject2();
    Input = Sinewave1 + Sinewave2;
    NoisyInput = Input + 0.001*randn(1024,1);
    SA(NoisyInput);
end
release(SA);

ズームすると、15 Hz 離れている 2 つのピークを区別できるようになりました。

周波数分解能を向上させると、時間分解能が低下します。周波数分解能と時間分解能の適切なバランスを維持するには、RBWSource プロパティを Auto に変更します。

ストリーミング中に、入力のプロパティまたはスペクトルアナライザーのプロパティを変更して、スペクトルアナライザーの出力に与える影響を即座に確認することができます。たとえば、ループのインデックスが 1000 の倍数であるときに、2 番目の正弦波の周波数を変更します。

release(Sineobject2);
SA.RBWSource = 'Auto';
for Iter = 1:5000
    Sinewave1 = Sineobject1();
    if (mod(Iter,1000) == 0)
        release(Sineobject2);
        Sineobject2.Frequency = Iter;
        Sinewave2 = Sineobject2();
    else
        Sinewave2 = Sineobject2();
    end
    Input = Sinewave1 + Sinewave2;
    NoisyInput = Input + 0.001*randn(1024,1);
    SA(NoisyInput);
end
release(SA);

ストリーミングループの実行中、2 番目の正弦波のピークが反復値に従って変化することを確認できます。同様に、シミュレーションの実行中にスペクトルアナライザーの任意のプロパティを変更して、それに対応する出力の変化を確認できます。

単位間のパワーの変換

スペクトルアナライザーでは、パワースペクトル密度を指定するための次の 3 つの単位が提供されています。[Watts/Hz]、[dBm/Hz]、および [dBW/Hz]。対応するパワーの単位は [Watts]、[dBm]、および [dBW] です。電気工学アプリケーションでは、信号の RMS を [Vrms] または [dBV] で表示することもできます。既定のスペクトルタイプは [dBm] の [パワー] です。

ワット単位から dBW 単位および dBm 単位へのパワーの変換

[dBW] 単位のパワーは次で求められます。

$P_{dBW} = 10 \log 10 (power in watt / 1 watt)$

[dBm] 単位のパワーは次で求められます。

$P_{dBm} = 10 \log_{10} (power in watt / 1 milliwatt)$

振幅が 1 V の正弦波信号の場合、[Watts] 単位での片側スペクトルのパワーは次で求められます。

$\begin{array}{l} P_{Watts} = A^{2} / 2 \\ P_{Watts} = 1 / 2 \end{array}$

この例では、このパワーは 0.5 W に等しくなります。対応する dBm 単位のパワーは次で求められます。

$\begin{array}{l} P_{dBm} = 10 \log_{10} (power in watt / 1 milliwatt) \\ P_{dBm} = 10 \log_{10} (0.5 / 10^{- 3}) \\ P_{dBm} = 26.9897 dBm \end{array}$

ここで、パワーは 26.9897 dBm に等しくなります。ピークの検出でこの値を確認するには、[ツール] 、 [測定値] 、 [ピークの検出] をクリックします。

ホワイトノイズ信号の場合、スペクトルはすべての周波数でフラットになります。この例のスペクトルアナライザーは、[0 Fs/2] の範囲の片側スペクトルを表示します。分散 1e-4 のホワイトノイズ信号の場合、単位帯域幅あたりのパワー (P_{unitbandwidth}) は 1e-4 です。周波数範囲全体でのワット単位のホワイトノイズの合計パワーは次で求められます。

周波数ビンの数は、全帯域幅の RBW に対する比率です。片側スペクトルの場合、全帯域幅はサンプリングレートの半分です。この例の RBW は 21.53 Hz です。これらの値を使用すると、ワット単位でのホワイトノイズの合計パワーは 0.1024 W です。dBm 単位では、ホワイトノイズのパワーは 10*log10(0.1024/10^-3) を使用して計算することができ、20.103 dBm に等しくなります。

ワット単位から dBFS 単位へのパワーの変換

スペクトル単位を [dBFS] に設定し、フルスケール (FullScaleSource) を [Auto] に設定すると、[dBFS] 単位のパワーは次のように計算されます。

$P_{dBFS} = 20 \cdot \log_{10} (\sqrt{P_{watts}} / Full_Scale)$

。ここでは以下のとおりです。

P_watts はワット単位のパワー。
double および float の信号では、Full_Scale は入力信号の最大値。
固定小数点または整数の信号では、Full_Scale は表現できる最大の値。

手動のフルスケールを指定した場合 (FullScaleSource を [Property] に設定)、[dBFS] 単位のパワーは次で求められます。

$P_{FS} = 20 \cdot \log_{10} (\sqrt{P_{watts}} / FS)$

ここで、FS は FullScale プロパティで指定されたフルスケーリング係数です。

振幅が 1 V の正弦波信号の場合、[Watts] 単位での片側スペクトルのパワーは次で求められます。

$\begin{array}{l} P_{Watts} = A^{2} / 2 \\ P_{Watts} = 1 / 2 \end{array}$

この例では、このパワーは 0.5 W に等しく、正弦波の最大入力信号は 1 V です。対応する dBFS 単位のパワーは次で求められます。

$\begin{array}{l} P_{FS} = 20 \cdot \log_{10} (\sqrt{1 / 2} / 1) \\ P_{FS} = - 3.0103 dBFS \end{array}$

ここで、パワーは -3.0103 に等しくなります。この値をスペクトルアナライザーで確認するには、次のコマンドを実行します。

Fs = 1000;  % Sampling frequency
sinef = dsp.SineWave('SampleRate',Fs,'SamplesPerFrame',100);
scope = dsp.SpectrumAnalyzer('SampleRate',Fs,...
   'SpectrumUnits','dBFS','PlotAsTwoSidedSpectrum',false)
%%
for ii = 1:100000
xsine = sinef();
scope(xsine)
end

次に、[ツール] 、 [測定値] 、 [ピークの検出] をクリックします。

dBm 単位のパワーから Vrms 単位の RMS への変換

[dBm] 単位のパワーは次で求められます。

$P_{dBm} = 10 \log_{10} (power in watt / 1 milliwatt)$

RMS の電圧は次で求められます。

$V_{rms} = 10^{P_{dBm} / 20} \sqrt{10^{- 3}}$

前の例では、P_dBm は 26.9897 dBm と同等です。V_rms は次のように計算されます。

$V_{rms} = 10^{26.9897 / 20} \sqrt{0.001}$

0.7071 と等しくなります。

この値を確認するには、次を行います。

[タイプ] を [RMS] に変更します。
[ツール] 、 [測定値] 、 [ピークの検出] をクリックして、ピークの検出を開きます。

dsp.SpectrumEstimator を使用したパワースペクトルの推定

スクリプトを開く

あるいは、dsp.SpectrumEstimator System object を使用して信号のパワースペクトルを計算することもできます。スペクトル推定器の出力を取得してデータを保存し、その後の処理で使用することができます。Estimation ライブラリ内の他のオブジェクトを表示するには、MATLAB® コマンドプロンプトで help dsp と入力して Estimation をクリックします。

初期化

dsp.SpectrumAnalyzer の使用に関する前の節と同じソースを使って、パワースペクトルを推定します。入力正弦波は 2 つの周波数 (1 つは 1000 Hz、もう 1 つは 5000 Hz) をもちます。dsp.SpectrumEstimator を初期化し、フィルターバンクアプローチを使用して信号のパワースペクトルを計算します。dsp.ArrayPlot オブジェクトを使用して信号のパワースペクトルを表示します。

Fs = 44100;
Sineobject1 = dsp.SineWave('SamplesPerFrame',1024,'PhaseOffset',10,...
    'SampleRate',Fs,'Frequency',1000);
Sineobject2 = dsp.SineWave('SamplesPerFrame',1024,...
    'SampleRate',Fs,'Frequency',5000);

SpecEst = dsp.SpectrumEstimator('Method','Filter bank',...
    'PowerUnits','dBm','SampleRate',Fs,'FrequencyRange','onesided');
ArrPlot = dsp.ArrayPlot('PlotType','Line','ChannelNames',{'Power spectrum of the input'},...
    'YLimits',[-80 30],'XLabel','Number of samples per frame','YLabel',...
    'Power (dBm)','Title','One-sided power spectrum with respect to samples');

推定

ストリーミングを行い、信号のパワースペクトルを推定します。for ループを作成して、5000 回の反復を実行します。各反復では、各正弦波の 1024 サンプル (1 フレーム) をストリーミングして、各フレームのパワースペクトルを計算します。ゼロ平均、標準偏差 0.001 のガウスノイズを入力信号に付加します。

for Iter = 1:5000
    Sinewave1 = Sineobject1();
    Sinewave2 = Sineobject2();
    Input = Sinewave1 + Sinewave2;
    NoisyInput = Input + 0.001*randn(1024,1);
    PSoutput = SpecEst(NoisyInput);
    ArrPlot(PSoutput);
end

フィルターバンクアプローチを使用すると、スペクトル推定の分解能は高くなり、ピークはスペクトル漏れのない正確なものになります。

x 軸を変換して周波数を表現

既定では、配列プロットはフレームごとのサンプル数についてのパワースペクトルデータを表示します。x 軸の点の数は入力フレームの長さと等しくなります。スペクトルアナライザーは周波数に対してパワースペクトルデータをプロットします。片側スペクトルの場合、周波数は [0 Fs/2] の範囲で変化します。両側スペクトルの場合、周波数は [-Fs/2 Fs/2] の範囲で変化します。配列プロットの x 軸をサンプルベースから周波数ベースに変換するには、以下を実行します。

[コンフィギュレーションプロパティ] アイコンをクリックします。
片側スペクトルの場合 - [メイン] タブで、[Sample increment] をに設定し、[X オフセット] を 0 に設定します。
両側スペクトルの場合 - [メイン] タブで、[Sample increment] をに設定し、[X オフセット] をに設定します。

この例では、スペクトルは片側であるため、[Sample increment] と [X オフセット] はそれぞれ 44100/1024 と 0 に設定されます。周波数を kHz 単位で指定するには、[Sample increment] を 44.1/1024 に設定します。

ArrPlot.SampleIncrement = (Fs/1000)/1024;
ArrPlot.XLabel = 'Frequency (kHz)';
ArrPlot.Title = 'One-sided power spectrum with respect to frequency';

for Iter = 1:5000
    Sinewave1 = Sineobject1();
    Sinewave2 = Sineobject2();
    Input = Sinewave1 + Sinewave2;
    NoisyInput = Input + 0.001*randn(1024,1);
    PSoutput = SpecEst(NoisyInput);
    ArrPlot(PSoutput);
end

ライブ処理

dsp.SpectrumEstimator オブジェクトの出力にはスペクトルデータが含まれており、その後の処理で使用できます。このデータはリアルタイムで処理することも、ワークスペースに格納することもできます。