ローパス FIR フィルターの設計
この例では、ローパス FIR フィルターの設計法を説明します。ここで説明する多くの概念は、ハイパス、バンドパスなどの他の応答にも拡張できます。
FIR フィルターが広く使用されているのは、そのようなフィルターを設計するための強力な設計アルゴリズムが存在するためです。また、これらのフィルターは、非再帰形式で実装すると本質的に安定しており、線形位相を簡単に得ることができ、マルチレートのケースにも拡張できます。さらに、それらのフィルターをサポートするハードウェアが豊富に存在します。この例では、ローパス FIR フィルターの設計に使用できる DSP System Toolbox™ の関数とオブジェクトについて紹介します。
ローパス FIR フィルター係数の取得
MATLAB でのローパス フィルター設計の例では、ローパス フィルターの設計で一般的に使用される DSP System Toolbox のコマンドライン ツールのいくつかを紹介しています。この例では、ツールボックスでローパス フィルターの設計に使用できる設計オプションについて、より全体的な概要を示します。まず、この例では、FIR フィルター係数のベクトルを返す 2 つの関数firceqripおよびfirgrを紹介します。firceqrip は、フィルター次数 (フィルター長と同様) が既知で固定の場合に使用します。
N = 100; % FIR filter order Fp = 20e3; % 20 kHz passband-edge frequency Fs = 96e3; % 96 kHz sampling frequency Rp = 0.00057565; % Corresponds to 0.01 dB peak-to-peak ripple Rst = 1e-4; % Corresponds to 80 dB stopband attenuation eqnum = firceqrip(N,Fp/(Fs/2),[Rp Rst],'passedge'); % eqnum = vec of coeffs filterAnalyzer(eqnum,SampleRate=Fs) % Visualize filter

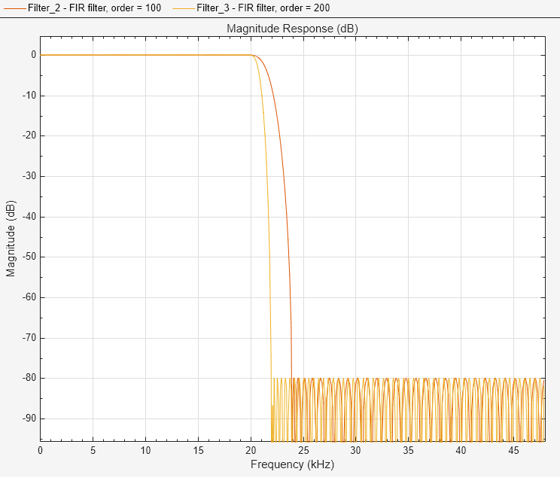
前の手順では、フィルター次数を任意に 100 と設定しました。一般に、大きい次数の方が理想のフィルターに近くなりますが、実装がコスト高になります。フィルター次数を 2 倍にすると、フィルターの遷移幅が半分に減ります (その他のすべてのパラメーターが同じままである場合)。
N2 = 200; % Change filter order from 100 to 200 eqNum200 = firceqrip(N2,Fp/(Fs/2),[Rp Rst],'passedge'); fvt = filterAnalyzer(eqnum,1,eqNum200,1,SampleRate=Fs); setLegendStrings(fvt, "FIR filter, order = "+[N N2])
最小次数ローパス フィルターの設計
フィルター次数を指定する代わりに、firgr を使用して設計仕様を満たすために最小限必要な次数を判断できます。そのためには、阻止帯域エッジ周波数を設定して遷移領域の幅を指定します。
Fst = 23e3; % Transition Width = Fst - Fp numMinOrder = firgr('minorder',[0,Fp/(Fs/2),Fst/(Fs/2),1],[1 1 0 0],... [Rp Rst]); fvt = filterAnalyzer(eqnum,1,eqNum200,1,numMinOrder,1,SampleRate=Fs); setLegendStrings(fvt,"FIR filter, order = "+[N N2 numel(numMinOrder)])
関数 firgr を使用して、偶数 ('mineven') または奇数 ('minodd') の最小次数フィルターを設計することもできます。
ローパス FIR フィルターの実装
フィルター係数を取得した後、dsp.FIRFilter System object™ を使用してフィルターを実装できます。この System object は、倍精度/単精度浮動小数点データだけでなく固定小数点データもサポートします。また、C コードおよび HDL コード生成に加え、ARM® Cortex® M および ARM Cortex A に最適化されたコード生成もサポートします。
lowpassFIR = dsp.FIRFilter(Numerator=eqnum); %or eqNum200 or numMinOrder
filterAnalyzer(lowpassFIR,SampleRate=Fs)
実際のフィルター処理を行うために、dsp.FIRFilter オブジェクトを関数と同様に直接呼び出します。このコードは、ガウス性ホワイト ノイズをフィルター処理し、結果のフィルター処理された信号を 10 秒間スペクトル アナライザーに表示します。
scope = spectrumAnalyzer(SampleRate=Fs,AveragingMethod='exponential',ForgettingFactor=0.5); show(scope); tic while toc < 10 x = randn(256,1); y = lowpassFIR(x); scope(y); end

フィルターの設計と実装を一度に実行
dsp.LowpassFilterSystem object を使用して、フィルターの設計と実装を 1 回の手順で行うこともできます。この System object は、浮動小数点、固定小数点、C コード生成および ARM Cortex M と ARM Cortex A の最適化コード生成もサポートしています。
lowpassFilt = dsp.LowpassFilter(DesignForMinimumOrder=false, ... FilterOrder=N,PassbandFrequency=Fp,SampleRate=Fs,... PassbandRipple=0.01, StopbandAttenuation=80); tic while toc < 10 x = randn(256,1); y = lowpassFilt(x); scope(y); end

System object は、フィルターの振幅を dB 単位で表します。通過帯域リップルを調べるには、フィルター アナライザーを使用します。
filterAnalyzer(lowpassFilt)

フィルター係数の取得
関数 tf を使用して、System object からフィルター係数を抽出します。
eqnum = tf(lowpassFilt);
調整可能なローパス FIR フィルター
実行時にカットオフ周波数が調整可能なローパス FIR フィルターを実装するには、dsp.VariableBandwidthFIRFilterオブジェクトを使用します。このフィルターは、フィルターの応答特性全体の制御を同じ精度で行うことはありませんが、動的周波数応答は可能です。
vbwFilter = dsp.VariableBandwidthFIRFilter(CutoffFrequency=1e3); tic told = 0; while toc < 10 t = toc; if floor(t) > told % Add 1 kHz every second vbwFilter.CutoffFrequency = vbwFilter.CutoffFrequency + 1e3; end x = randn(256,1); y = vbwFilter(x); scope(y); told = floor(t); end
詳細設計オプション: 最適な非等リップル ローパス フィルター
この例では、これまで最適な等リップル設計について説明してきました。等リップル設計は、理想的な応答からの標準偏差を均等に分散して最適化を達成します。これらの設計は最大偏差 (リップル) を最小限にするという利点があります。しかし、そのエネルギー面から測定した全体的な偏差が大きくなる傾向があり、それが常に望ましいとは限りません。信号をローパス フィルター処理する場合、阻止帯域の信号の残留エネルギーが比較的大きくなる可能性があります。これが問題になる場合に、阻止帯域のエネルギーを最小限にする最適な設計を提供するのが最小二乗法です。最小二乗フィルターやその他のローパス フィルターの設計には、designfilt の lowpassfir 応答を使用できます。最小二乗 FIR 設計を、フィルター次数と遷移幅が同じである FIR 等リップル設計と比較します。
lsFIR = designfilt("lowpassfir",FilterOrder=133,PassbandFrequency=Fp,StopBandFrequency=Fst, ... DesignMethod="ls",SampleRate=Fs,SystemObject=true); LP_MIN = dsp.FIRFilter(Numerator=numMinOrder); fvt = filterAnalyzer(LP_MIN,lsFIR.tf,SampleRate=Fs); setLegendStrings(fvt,["Equiripple design","Least-squares design"])
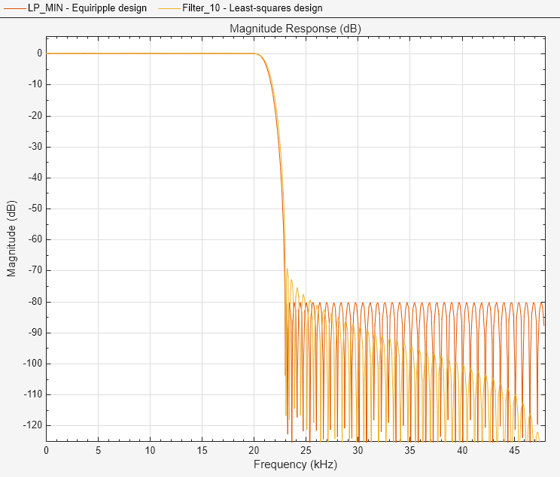
最小二乗法設計では阻止帯域の減衰量が周波数と共に増えますが、等リップル設計では一定です。最小二乗法の場合、減衰が大きくなることによって、信号をフィルター処理する帯域のエネルギーが最小化されます。
阻止帯域の減衰量が増大する等リップル設計
最小二乗法設計の望ましくない結果として、エッジ近くの通過帯域のリップルが大きくなる傾向があることです。ローパス フィルター全般では、フィルター処理する信号の通過帯域周波数への影響ができるだけ少ない方が望ましいとされています。この点で、通常は等リップル通過帯域が推奨されます。阻止帯域で減衰量を増やす必要がある場合は、等リップル設計オプションを使用してこれを達成できます。
FIR_eqrip_slope = designfilt("lowpassfir",FilterOrder=133,PassbandFrequency=Fp,StopBandFrequency=Fst, ... DesignMethod="equiripple",SampleRate=Fs,StopbandShape="1/f",StopbandDecay=4,SystemObject=true); fvt = filterAnalyzer(lsFIR,FIR_eqrip_slope); setLegendStrings(fvt,["Least-squares design",... "Equiripple design with stopband decaying as (1/f)^4"])

2 つの設計の阻止帯域はよく似ています。しかし、等リップル設計では、通過帯域エッジ周波数 20 kHz の近傍で通過帯域リップルが大幅に小さくなっています。
mls = measure(lsFIR); meq = measure(FIR_eqrip_slope); mls.Apass
ans = 0.0121
meq.Apass
ans = 0.0046
また、任意の振幅仕様を使用して 2 つの帯域 (1 つは通過帯域用、もう 1 つは阻止帯域用) を選択することで、阻止帯域の減衰量の増加を実装することもできます。次に、2 番目の帯域の重みを使用すると、帯域全体の減衰を増やせます。この設計やその他の任意振幅設計の詳細については、任意の振幅フィルター設計を参照してください。
B = 2; % Number of bands F = [0 Fp linspace(Fst,Fs/2,40)]; A = [1 1 zeros(1,length(F)-2)]; W = linspace(1,100,length(F)-2); lpfilter = designfilt("arbmagfir",FilterOrder=N,NumBands=B, ... BandFrequencies1=F(1:2),BandAmplitudes1=A(1:2), ... BandFrequencies2=F(3:end),BandAmplitudes2=A(3:end), ... BandWeights2=W,SampleRate=Fs, ... DesignMethod="equiripple",SystemObject=true); filterAnalyzer(lpfilter);
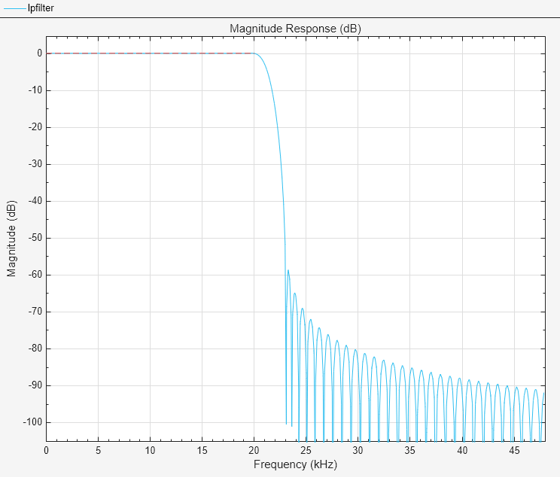
最小位相ローパス フィルターの設計
この例では、ここまで線形位相設計のみを考慮しました。線形位相は多くの用途に適しています。言うまでもなく、線形位相が必要条件でない場合は、最小位相設計の方が線形位相設計よりも大幅な改善を期待できます。しかし、最小位相設計は常に数値的信頼性が高いわけではありません。必ずフィルター アナライザーで設計をチェックしてください。
最小位相設計の利点を説明するため、同じ設計仕様を満たす線形位相設計と最小位相設計を比較します。
Fp = 20e3; Fst = 22e3; Fs = 96e3; Ap = 0.06; Ast = 80; linphaseSpec = designfilt("lowpassfir",PassbandFrequency=Fp,StopbandFrequency=Fst, ... PassbandRipple=Ap,StopbandAttenuation=Ast,SampleRate=Fs, ... DesignMethod="equiripple",SystemObject=true); eqripSpec = designfilt("lowpassfir",PassbandFrequency=Fp,StopbandFrequency=Fst, ... PassbandRipple=Ap,StopbandAttenuation=Ast,SampleRate=Fs, ... DesignMethod="equiripple",PhaseConstraint="minimum",SystemObject=true); fvt = filterAnalyzer(linphaseSpec,eqripSpec); setLegendStrings(fvt,... ["Linear-phase equiripple design",... "Minimum-phase equiripple design"])
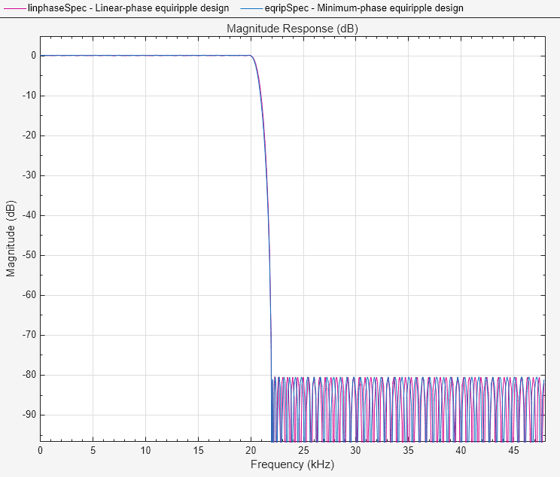
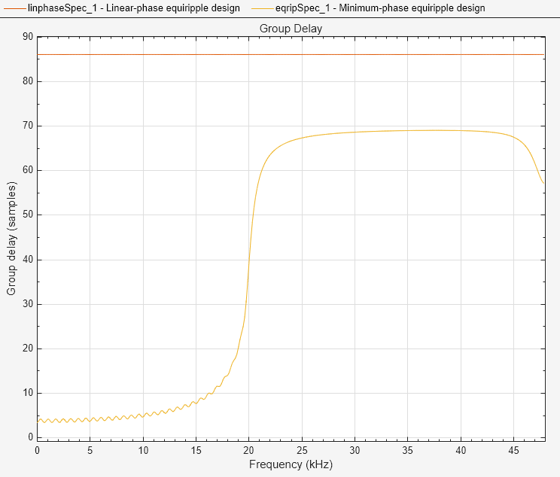
係数の数が 173 から 141 に減っています。群遅延プロットを作成し、群遅延が (特に通過帯域領域で) かなり小さくなっていることを確認します。
fvt = filterAnalyzer(linphaseSpec,eqripSpec,... Analysis='groupdelay'); setLegendStrings(fvt,... ["Linear-phase equiripple design",... "Minimum-phase equiripple design"])
多段手法を使用した最小次数ローパス フィルターの設計
最小位相設計に関連しない係数の数を最小化する別の方法に、多段手法の使用があります。この例では内挿 FIR (IFIR) 法を紹介します。このアプローチでは、設計問題をカスケード状の 2 つのフィルター設計に分割します。この例では、設計には 173 ではなく 151 の係数が必要です。多段設計法の詳細については、遷移帯域が狭い FIR フィルターの効率的な設計を参照してください。
内挿 FIR (IFIR) 設計アルゴリズムを使用してフィルターを設計します。フィルターの実装コストを計算します。
Fp = 20e3; Fst = 22e3; Fs = 96e3; Ap = 0.06; Ast = 80; interpFilter = designfilt("lowpassfir",PassbandFrequency=Fp,StopbandFrequency=Fst, ... PassbandRipple=Ap,StopbandAttenuation=Ast,SampleRate=Fs, ... DesignMethod="ifir",SystemObject=true); cost(interpFilter)
ans = struct with fields:
NumCoefficients: 151
NumStates: 238
MultiplicationsPerInputSample: 151
AdditionsPerInputSample: 149
フィルター アナライザーを使用して、IFIR 設計と線形位相設計を比較します。
fvt = filterAnalyzer(linphaseSpec,interpFilter); setLegendStrings(fvt,... ["Linear-phase equiripple design",... "Interpolated FIR equiripple design"]);

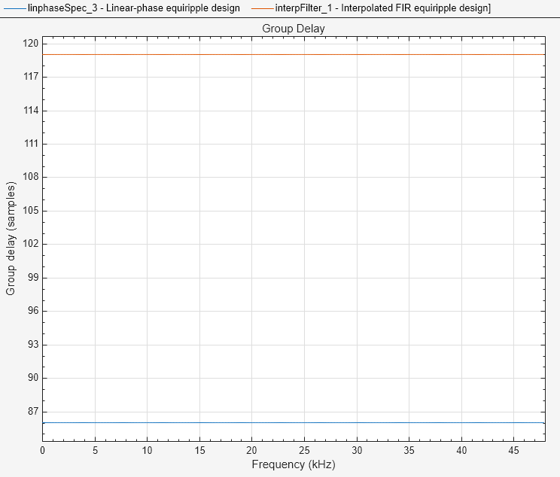
IFIR 設計の群遅延をプロットします。IFIR 設計では線形位相が提供されますが、一般的に群遅延は同等の単一ステージの設計よりも大きくなります。
fvt = filterAnalyzer(linphaseSpec,interpFilter,Analysis='groupdelay'); setLegendStrings(fvt,... ["Linear-phase equiripple design",... "Interpolated FIR equiripple design]"])
マルチレートの用途向けローパス フィルターの設計
ローパス フィルターは間引きや内挿の設計に広く用いられています。詳細については、Design of Decimators and Interpolatorsを参照してください。効率的な実装となる多段手法の詳細については、Multistage Rate Conversionを参照してください。