磁気浮上のモデル化

問題: 磁気浮上システムのモデル化

この例では、制御電流を使用する磁気浮上の動的動作を予測できるニューラル ネットワークの構築を試みます。

このシステムは、磁石の位置と制御電流によって特徴付けられます。この両方によって、直後の磁石の位置が決まります。

これは、時系列問題の例です。この例では、フィードバック時系列 (磁石の位置) と外部入力系列 (制御電流) の過去の値を使用して、フィードバック系列の将来の値を予測します。

ニューラル ネットワークを使用する理由

ニューラル ネットワークは、時系列問題に非常に適しています。十分な要素 (ニューロンと呼ばれる) が含まれるニューラル ネットワークは、任意の精度で動的システムをモデル化できます。特に、非線形動的問題への対応には非常に適しています。ニューラル ネットワークはこの問題を解くことのできる適切な候補であると言えます。

ネットワークは、制御電流に応じた浮上磁石の実際の位置の記録を使用して設計されます。

データの準備

入力時系列 X とターゲット時系列 T の 2 つの行列にデータを整理することによって、ニューラル ネットワークに関数近似問題用のデータを設定します。

入力系列 X は、各要素が制御電流の関連タイム ステップを示す行 cell 配列です。

ターゲット系列 T は、各要素が浮上磁石の位置の関連タイム ステップを示す行 cell 配列です。

ここで、このようなデータセットが読み込まれます。

[x,t] = maglev_dataset;

入力 X およびターゲット T のサイズを表示できます。

X と T の両方に 4001 の列があることに注意してください。これらは制御電流と磁石の位置の 4001 点のタイム ステップを表します。

size(x)

ans = 1×2

           1        4001

size(t)

ans = 1×2

           1        4001

ニューラル ネットワークを使用した時系列のモデル化

次の手順では、磁石の位置の変化のモデル化を学習するニューラル ネットワークを作成します。

ニューラル ネットワークはランダムな初期重みで開始するため、この例で得られる結果は実行するたびに多少異なります。このようなランダム性を回避するには、乱数シードを設定します。ただし、これはユーザー独自のアプリケーションには不要です。

setdemorandstream(491218381)

2 層 (1 つの隠れ層) の NARX ニューラル ネットワークは、隠れ層に十分なニューロンがある場合、任意の動的な入出力関係にあてはめることがきます。出力層ではない層は、隠れ層と呼ばれます。

この例では、10 個のニューロンがある 1 つの隠れ層を試します。一般的に、難しい問題ほど多くのニューロンが、そしておそらくは多くの層が必要になります。簡単な問題では、必要なニューロンが少なくなります。

さらに、外部入力 (制御電流) およびフィードバック (磁石の位置) に関する 2 つの遅延でタップ遅延を使用してみます。遅延が多いほど、より複雑な動的システムをネットワークでモデル化できます。

ネットワークはまだ入力データとターゲット データに一致するように構成されていないため、入力と出力のサイズは 0 です。ネットワークの学習時にはこのようになります。

出力 y(t) は入力でもあり、その遅延バージョンがネットワークにフィードバックされます。

net = narxnet(1:2,1:2,10);
view(net)

ネットワークの学習を行う前に、外部入力時系列とフィードバック時系列の最初の 2 つのタイム ステップを使用して、ネットワークの 2 つのタップ遅延状態を指定しなければなりません。

さらに、フィードバック系列を入力系列とターゲット系列の両方として使用する必要があります。

関数 PREPARETS は、シミュレーションおよび学習用の時系列データを準備します。Xs は、シフトした入力系列およびターゲット系列で構成され、ネットワークに提示されます。Xi は、初期の入力遅延状態です。Ai は、層の遅延状態 (この場合は層間の遅延がないので空)、Ts はシフトしたフィードバック系列です。

[Xs,Xi,Ai,Ts] = preparets(net,x,{},t);

これでネットワークの学習の準備が整いました。タイム ステップが自動的に学習セット、検証セット、およびテスト セットに分割されます。学習セットは、ネットワークに教えるために使用されます。検証セットに対してネットワークの改善が続いている限り、学習が続行されます。テスト セットを使用することで、ネットワークの精度を完全に独立して測定できます。

Neural Network Training Tool を使用すると、学習するネットワークと、学習に使用されているアルゴリズムが表示されます。さらに、学習中には学習の状態が表示され、学習を停止した条件が緑で強調表示されます。

下部にあるボタンを使用すると、便利なプロットを開くことができます。これらのプロットは、学習中および学習後に開くことができます。アルゴリズム名およびプロット ボタンの隣のリンクを使用すると、これらに関するドキュメンテーションを開くことができます。

[net,tr] = train(net,Xs,Ts,Xi,Ai);

学習中にネットワーク性能がどのように改善されているかを確認するには、学習ツールの [パフォーマンス] ボタンをクリックするか、PLOTPERFORM を呼び出します。

性能は、平均二乗誤差で測定され、対数スケールで表示されます。これは、ネットワークの学習が進むと急激に低下します。

性能は、学習セット、検証セット、およびテスト セットのそれぞれについて表示されます。

plotperform(tr)

ニューラル ネットワークのテスト

これですべてのタイム ステップについて学習済みニューラル ネットワークの平均二乗誤差を測定できるようになりました。

Y = net(Xs,Xi,Ai);

perf = mse(net,Ts,Y)

perf = 2.9245e-06

PLOTRESPONSE は、実際の磁石の位置と比較したネットワークの応答を表示します。モデルが正確な場合、'+' の点が菱形の点を追う形となり、下の軸に示す誤差が非常に小さくなります。

plotresponse(Ts,Y)

PLOTERRCORR は、時間 t の誤差 e(t) とさまざまなラグに対する誤差 e(t+lag) の相関を表示します。中心線は、平均二乗誤差を示します。ネットワークの学習が十分に行われている場合、他のすべての線が非常に短くなります。学習が十分に行われていない場合、すべての線が赤い信頼限界の範囲内になります。

誤差を計算するには、関数 GSUBTRACT を使用します。この関数は、減算を一般化して cell 配列データ間の差をサポートしています。

E = gsubtract(Ts,Y);

ploterrcorr(E)

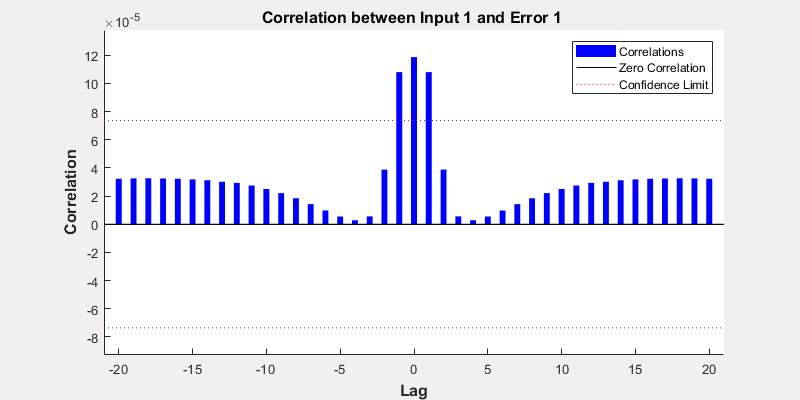
同様に、PLOTINERRCORR は、さまざまなラグで入力に対する誤差の相関を表示します。この場合、中心線を含むほとんどまたはすべての線が信頼限界の範囲内になります。

plotinerrcorr(Xs,E)

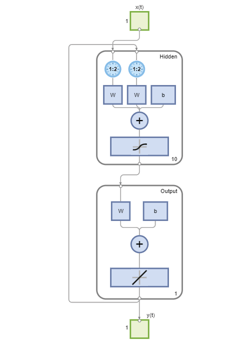
ネットワークの学習は、ターゲットがフィードバック入力として使用される開ループ形式で行いました。ネットワークを変換して、独自の予測がフィードバック入力になる閉ループ形式にすることもできます。

net2 = closeloop(net);
view(net2)

閉ループ形式でネットワークのシミュレーションを行うことができます。この場合、ネットワークには磁石の初期位置のみが指定されるため、独自の予測位置を再帰的に使用して新しい位置を予測しなければなりません。

この場合すぐに、予測した応答と実際の応答が一致しなくなります。モデルが非常に適切な場合でも、このような状況が発生します。ただし、一致していたステップ数を確認すると、興味深い点が見えてきます。

ここでも、PREPARETS によって、ネットワークの変更を考慮に入れて時系列データの準備が行われます。

[Xs,Xi,Ai,Ts] = preparets(net2,x,{},t);
Y = net2(Xs,Xi,Ai);
plotresponse(Ts,Y)

実際の発生時より 1 タイム ステップ早く磁石の予測位置にアクセスする必要がある場合は、ネットワークから遅延を削除できます。これにより、任意の時間 t で時間 t+1 の位置の推定が出力されます。

net3 = removedelay(net);
view(net3)

ここでも、関数 PREPARETS を使用して、シミュレーション用の時系列を準備します。今回も、開ループで予測が行われているためネットワークは非常に正確ですが、出力は 1 タイム ステップ分シフトします。

[Xs,Xi,Ai,Ts] = preparets(net3,x,{},t);
Y = net3(Xs,Xi,Ai);
plotresponse(Ts,Y)

この例では、動的磁気浮上システムの動作をモデル化するニューラル ネットワークを設計する方法を説明しました。

ニューラル ネットワークとそのアプリケーションの詳細は、他の例およびドキュメンテーションを参照してください。