アヤメのクラスタリング

問題: アヤメの花のクラスタリング

この例では、類似のクラスがグループとしてまとめられるように、アヤメの花を自然なクラスにクラスタリングするニューラル ネットワークの構築を試みます。アヤメはそれぞれ以下の 4 つの特徴で表されます。

このクラスタリング問題の例では、標本の類似性に基づいて標本を複数のクラスにグループ化します。既知の入力に対してクラス定義を作成するだけでなく、不明な入力も適宜分類できるニューラル ネットワークを作成します。

自己組織化マップ ニューラル ネットワークを使用する理由

自己組織化マップ (SOM) は、分類の作成に非常に適しています。さらに、他のクラスと比較して最も類似性のあるクラスはどれかを示すトポロジカルな情報が分類に保持されます。自己組織化マップは、目的に応じた詳細レベルで作成できます。これは特に、次元数が大きく、複雑な形状をした複雑に結合された特徴空間におけるデータのクラスタリングに非常に適しています。アヤメの花のクラスタリングには非常に適しています。

花の 4 つの属性が SOM への入力となり、SOM でニューロンの 2 次元の層にマッピングされます。

データの準備

入力行列 X にデータを整理することによって、SOM にクラスタリング問題用のデータを設定します。

入力行列の i 番目の列にはそれぞれ、1 つの花から得られる 4 つの測定値を表す 4 つの要素が含まれます。

ここで、このようなデータセットが読み込まれます。

x = iris_dataset;

入力 X のサイズを表示できます。

X に 150 の列があることに注意してください。これらは 150 組のアヤメの花の属性を表します。4 つの測定値に対する 4 つの行があります。

size(x)

ans = 1×2

     4   150

ニューラル ネットワークを使用したクラスタリング

次の手順では、クラスタリングを学習するニューラル ネットワークを作成します。

selforgmap は、層の各次元のニューロンの数を選択することによって必要に応じた詳細レベルで標本を分類できる、自己組織化マップを作成します。

この例では、8x8 の六角形のグリッドに配置された 64 個のニューロンがある 2 次元の層を試します。一般的に、ニューロンの数と次元数が増加して詳細レベルが高くなると、より複雑な特徴空間のトポロジのモデル化が可能になります。

ネットワークはまだ入力データに一致するように構成されていないため、入力のサイズは 0 です。ネットワークの学習時にはこのようになります。

net = selforgmap([8 8]);
view(net)

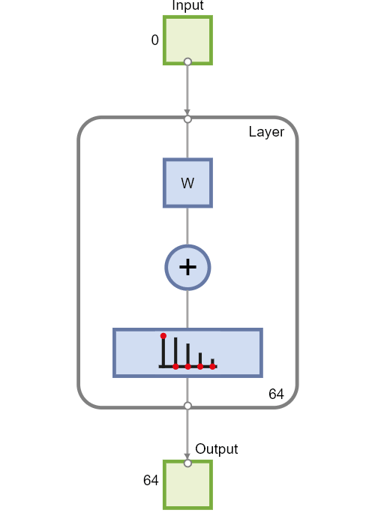
これで train を使用したネットワーク最適化の準備が整いました。

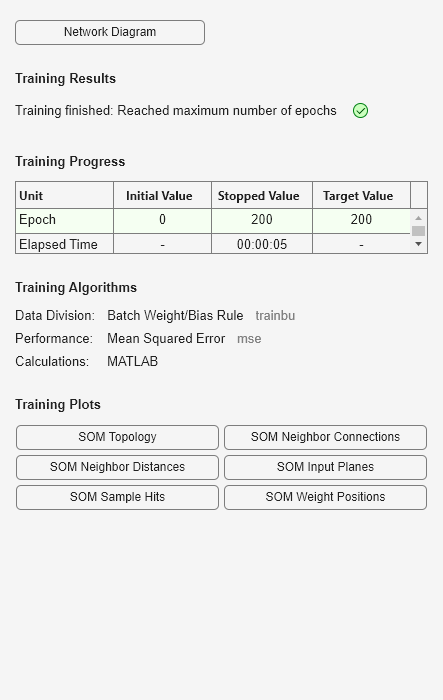
Neural Network Training Tool を使用すると、学習するネットワークと、学習に使用されているアルゴリズムが表示されます。さらに、学習中には学習の状態が表示され、学習を停止した条件が緑で強調表示されます。

下部にあるボタンを使用すると、便利なプロットを開くことができます。これらのプロットは、学習中および学習後に開くことができます。アルゴリズム名およびプロット ボタンの隣のリンクを使用すると、これらに関するドキュメンテーションを開くことができます。

[net,tr] = train(net,x);

ここで、自己組織化マップを使用して、各学習入力のクラス ベクトルが計算されます。これらの分類は既知の花によって与えられた特徴空間を対象としていますが、新しい花を適宜分類するためにも使用できます。ネットワークの出力は 64 行 150 列の行列です。i 番目の列はそれぞれ、j 番目の要素が 1 であれば i 番目の入力ベクトルが j 番目のクラスターに属することを表します。

関数 vec2ind は、各ベクトルについて、出力が 1 のニューロンのインデックスを返します。64 個のニューロンで表される 64 個のクラスターの場合、インデックスの範囲は 1 ～ 64 になります。

y = net(x);
cluster_index = vec2ind(y);

plotsomtop は、8x8 の六角形のグリッドに配置された 64 個のニューロンの自己組織化マップ トポロジをプロットします。各ニューロンは、異なるクラスの花を表すように学習済みです。一般的に隣接するニューロンは類似するクラスを表します。

plotsomtop(net)

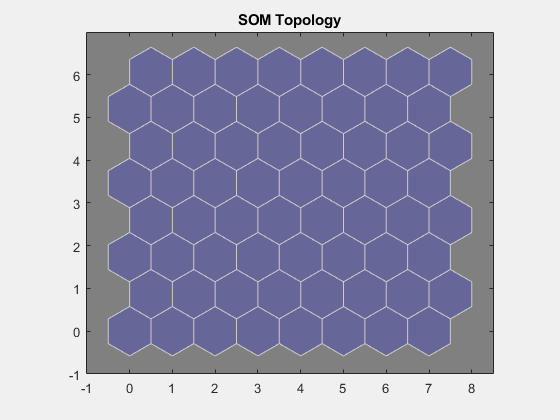
plotsomhits は、それぞれの花のクラスを計算し、各クラスの花の数を示します。ヒット数が多いニューロンの領域は、特徴空間において密度の高い類似の領域を表すクラスを示します。一方、ヒット数が少ない領域は、特徴空間において密度の低い領域を示します。

plotsomhits(net,x)

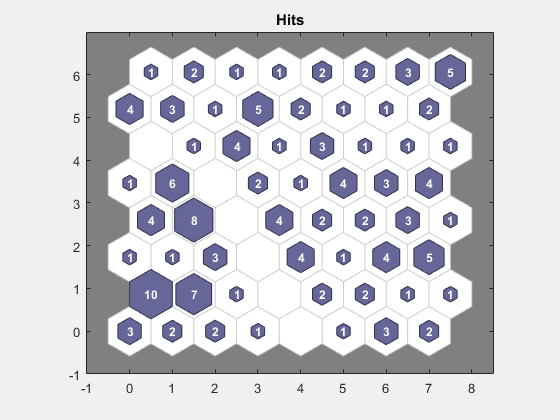
plotsomnc は、ニューロンの近傍結合を表示します。通常、近傍によって類似の標本が分類されます。

plotsomnc(net)

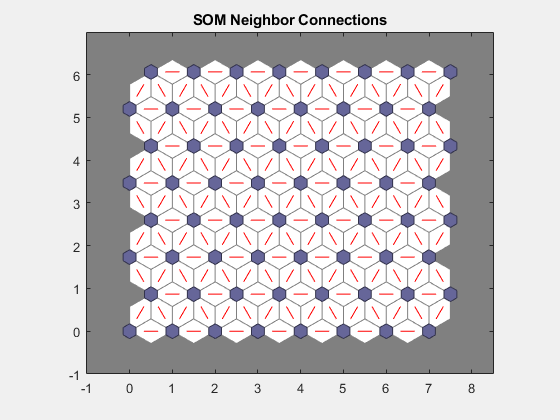
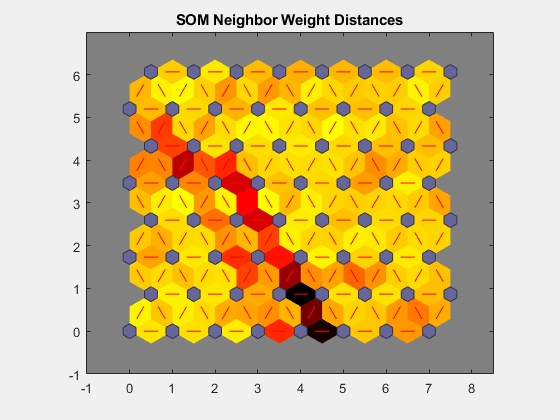
plotsomnd は、各ニューロンのクラスの近傍からの距離 (ユークリッド距離) を表示します。薄い色の結合は、密接に結合した入力空間の領域を示します。一方、濃い色の結合は、間隔が広く、間に花が少ないかまったくない特徴空間の領域を表すクラスを示します。

濃い色の結合によって長い境界線が形成され、入力空間の大きな領域が区切られている場合、境界線のそれぞれの側のクラスが大きく異なる特徴を持つ花を表していることを示します。

plotsomnd(net)

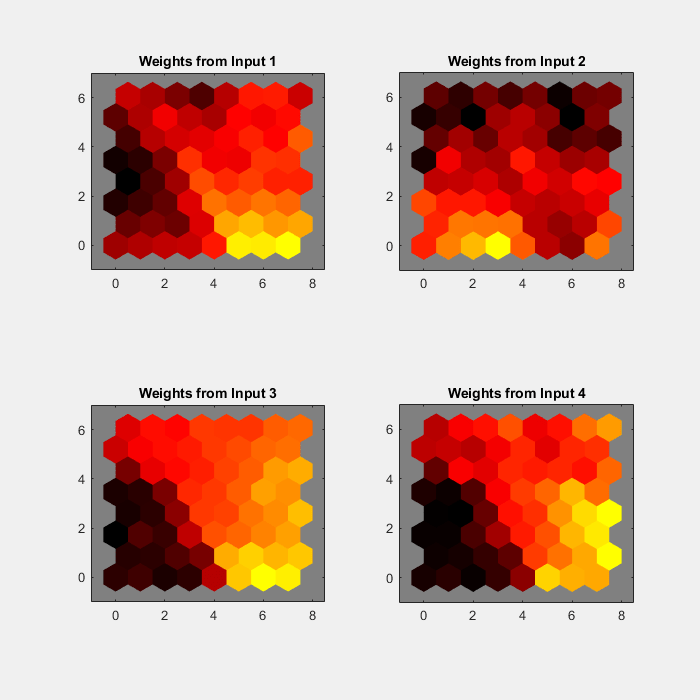
plotsomplanes は、4 つの入力特徴のそれぞれの重み平面を表示します。これらは、8x8 の六角形のグリッドに配置された 64 個のニューロンに各入力を結合する重みを可視化したものです。色が濃いほど、重みが大きいことを表します。2 つの入力の重み平面が似ている (色のグラデーションが同じか逆である) 場合、高い相関があることを示します。

plotsomplanes(net)

この例では、4 つの特性に基づいてアヤメの花をクラスタリングするニューラル ネットワークを設計する方法を説明しました。

ニューラル ネットワークとそのアプリケーションの詳細は、他の例およびドキュメンテーションを参照してください。