カニの分類

問題: カニの分類

この例では、カニの身体測定値からカニの性別を特定できる分類器の作成を試みます。カニの 6 つの身体的特性 (種、前縁、後面の幅、全長、幅、高さ) を考慮に入れます。この問題は、これらの 6 つの身体的特性の観測値が与えられた場合にカニの性別を特定するものです。

ニューラル ネットワークを使用する理由

ニューラル ネットワークは優れた分類器であることが証明されており、特に、非線形問題への対応に適しています。カニの分類のような実際の現象には非線形特性があるため、ニューラル ネットワークがこの問題を解くことのできる適切な候補であることは確実です。

6 つの身体的特性がニューラル ネットワークへの入力となり、カニの性別がターゲットとなります。カニの身体的特性に対する 6 つの観測値で構成される入力を指定したときに、ニューラル ネットワークによってカニがオスであるかメスであるかが特定される必要があります。

このために、以前に記録した入力をニューラル ネットワークに提示して、目標のターゲット出力を生成するように調整します。このプロセスは、ニューラル ネットワークの学習と呼ばれます。

データの準備

入力行列 X とターゲット行列 Y の 2 つの行列にデータを整理することによって、ニューラル ネットワークに分類問題用のデータを設定します。

入力行列の i 番目の列にはそれぞれ、カニの種、前縁、後面の幅、全長、幅、高さを表す 6 つの要素が含まれます。

ターゲット行列の対応する各列には、2 つの要素が含まれます。メスのカニは最初の要素の 1 で表され、オスのカニは 2 番目の要素の 1 で表されます (その他のすべての要素は 0 です)。

ここで、データセットが読み込まれます。

[x,t] = crab_dataset;
size(x)

ans = 1×2

     6   200

size(t)

ans = 1×2

     2   200

ニューラル ネットワーク分類器の作成

次の手順では、カニの性別の特定を学習するニューラル ネットワークを作成します。

ニューラル ネットワークはランダムな初期重みで開始するため、この例で得られる結果は実行するたびに多少異なります。このようなランダム性を回避するには、乱数シードを設定します。ただし、これはユーザー独自のアプリケーションには不要です。

setdemorandstream(491218382)

2 層 (1 つの隠れ層) のフィードフォワード ニューラル ネットワークは、隠れ層に十分なニューロンがある場合、任意の入出力関係を学習できます。出力層ではない層は、隠れ層と呼ばれます。

この例では、10 個のニューロンがある 1 つの隠れ層を試します。一般的に、難しい問題ほど多くのニューロンが、そしておそらくは多くの層が必要になります。簡単な問題では、必要なニューロンが少なくなります。

ネットワークはまだ入力データとターゲット データに一致するように構成されていないため、入力と出力のサイズは 0 です。ネットワークの学習時にはこのようになります。

net = patternnet(10);
view(net)

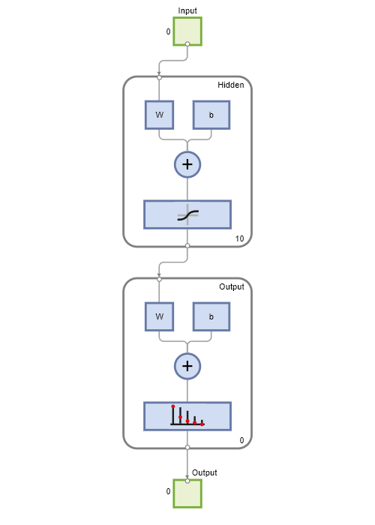
これでネットワークの学習の準備が整いました。標本が学習セット、検証セット、およびテスト セットに自動的に分割されます。学習セットは、ネットワークに教えるために使用されます。検証セットに対してネットワークの改善が続いている限り、学習が続行されます。テスト セットを使用することで、ネットワークの精度を完全に独立して測定できます。

[net,tr] = train(net,x,t);

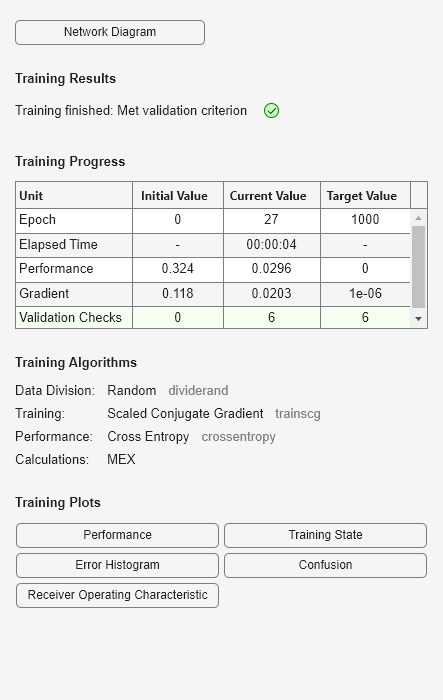
学習中にネットワーク性能がどのように改善されているかを確認するには、学習ツールの [パフォーマンス] ボタンをクリックするか、PLOTPERFORM を呼び出します。

性能は、平均二乗誤差で測定され、対数スケールで表示されます。これは、ネットワークの学習が進むと急激に低下します。

性能は、学習セット、検証セット、およびテスト セットのそれぞれについて表示されます。

plotperform(tr)

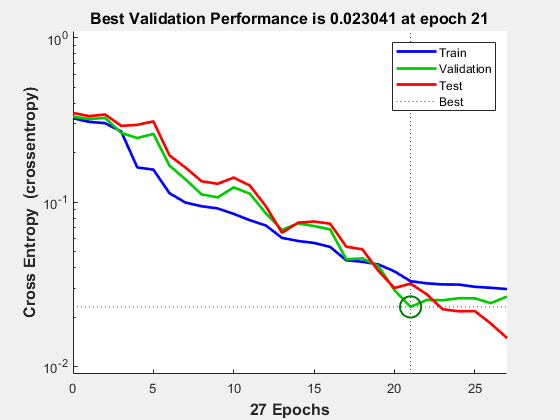
分類器のテスト

テスト標本を使用して、学習済みニューラル ネットワークをテストできるようになりました。これにより、実際のデータに適用した場合にネットワークがどの程度一致しているかを把握できます。

ネットワーク出力は 0 ～ 1 の範囲になるため、関数 vec2ind を使用して、各出力ベクトルで最大の要素の位置としてクラス インデックスを取得できます。

testX = x(:,tr.testInd);
testT = t(:,tr.testInd);

testY = net(testX);
testIndices = vec2ind(testY)

testIndices = 1×30

     2     2     2     1     2     2     2     1     2     2     2     2     1     1     2     2     2     1     2     2     1     2     1     1     1     1     1     2     2     1

ニューラル ネットワークがどの程度データに当てはまるかを測定する方法の 1 つは、混同プロットです。ここで、すべての標本に対して混同行列がプロットされます。

混同行列は、正しい分類と正しくない分類の比率を示します。正しい分類は、行列の対角部分の緑の正方形に表示されます。正しくない分類は、赤い正方形に表示されます。

ネットワークが適切な分類を学習した場合、赤い正方形の比率は非常に小さくなり、誤分類がほとんどないことを示します。

そうなっていない場合は、追加学習を行うか、隠れニューロンを増やしてネットワークの学習を行うことをお勧めします。

plotconfusion(testT,testY)

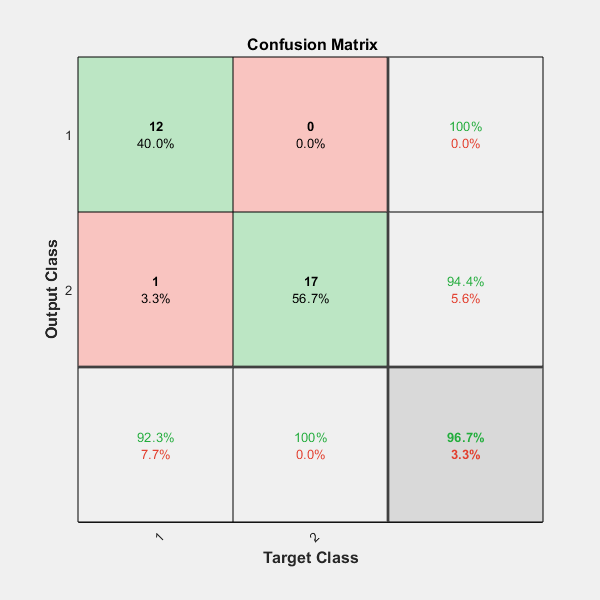
正しい分類と正しくない分類の全体的な比率を次に示します。

[c,cm] = confusion(testT,testY)

c = 0.0333

cm = 2×2

    12     1
     0    17

fprintf('Percentage Correct Classification   : %f%%\n', 100*(1-c));

Percentage Correct Classification   : 96.666667%

fprintf('Percentage Incorrect Classification : %f%%\n', 100*c);

Percentage Incorrect Classification : 3.333333%

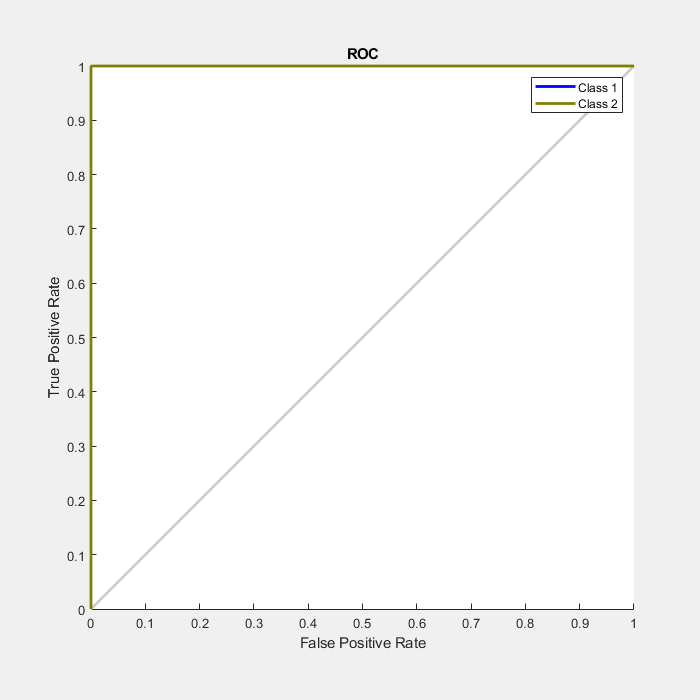
ニューラル ネットワークがどの程度データに当てはまるかを測定するもう 1 つの方法は、受信者動作特性プロットです。これは、出力のしきい値が 0 ～ 1 の範囲で変化する場合に偽陽性率と真陽性率にどのような関連があるかを示します。

線が左上にあればあるほど、高い真陽性率を得るために受け入れる必要がある偽陽性の数が減少します。最適な分類器とは、線が左下隅から左上隅、右上隅、またはその近くに向かって伸びている分類器です。

plotroc(testT,testY)

この例では、ニューラル ネットワークを使用したカニの分類について説明しました。

ニューラル ネットワークとそのアプリケーションの詳細は、他の例およびドキュメンテーションを参照してください。