B 型

B 型の紹介

一変量スプライン f は、非減少の節点シーケンス t と B スプライン係数シーケンス a によって指定されます。多変量スプラインの詳細については、多変量テンソル積スプラインを参照してください。係数は、(列) ベクトル、行列や、場合によっては N 次元配列である可能性もあります。係数が 2 ベクトルまたは 3 ベクトルの場合、f は R² または R³ 内の曲線で、係数は曲線の "制御点" と呼ばれます。

大まかに言うと、このようなスプラインは、特定の次数であり、ブレーク t(i) をもつ区分的多項式です。ただし、節点は、繰り返されることがあるという点でブレークとは異なります。つまり、t は "厳密" に増加する必要はありません。以下で説明するとおり、最終的な節点の "多重度" が、複数の節点にわたるスプラインの滑らかさを制御します。

[d,n] = size(a) および n+k = length(t) の場合、スプラインは "次数" k です。つまり、その多項式区分は次数 < k となります。たとえば、3 次多項式を指定するために 4 つの係数が必要なので、"3 次" スプラインは "4 次" のスプラインです。

B 型の定義

B 型スプライン f は、4 つの項 t、a、n、k によって構成されます。

つまり、明示すると次のようになります。

$$f={\displaystyle \sum _{i=1}^n{B}_{i,k}a\left(:,i\right)}$$

B_i,k=B(·|t(i:i+k)) は、与えられた節点シーケンス t に対する次数 k の i 番目の B スプラインです。つまり、節点 t(i),...,t(i+k) を持つ B スプラインです。この B 型の基本区間は区間 [t(1)..t(n+k)] です。これは、コマンド fnplt によって B 型のスプラインがプロットされる既定の区間です。B 型のスプラインは基本区間外では 0 ですが、fn2fm によって pp 型に変換すると通常はこれが当てはまらなくなることに注意してください。これは、基本区間外では、最初または最後の多項式区分の拡張によって区分的多項式が定義されるためです。特に、B 型の関数では、そのすべての内部節点 (つまり、t(1)<t(i)<t(n+k) である t(i)) だけでなく、両端の節点 t(1) および t(n+k) においても、値またはいずれかの微分にジャンプが含まれる場合があります。

B 型および B スプライン

B 型のスプラインの基本ブロックは B スプラインです。次数 4 の B スプラインおよびそれを構成する 4 つの 3 次多項式には、節点シーケンスが [0 1.5 2.3 4 5] で次数が 4 の B スプラインと、B スプラインを構成する区分をもつ多項式と共に示されています。図に関する情報は、次のコマンドで生成できます。

bspline([0 1.5 2.3 4 5])

次数 4 の B スプラインおよびそれを構成する 4 つの 3 次多項式

要約: 節点 t(i)≤····≤ t(i+k) をもつ B スプラインは、区間 (t(i)..t(i+k)) では正になり、この区間外では 0 になります。これは、サイト t(i),...,t(i+k) にブレークがある次数 k の区分的多項式です。これらの節点は一致する場合があります。正確な "多重度" によって、2 つの多項式区分が結合する際の平滑性が制御されます。

B スプラインの定義

省略形

$$f\in S_{k,t}$$

は、f が節点シーケンス t をもつ次数 k のスプラインである、つまり、節点シーケンス t で次数 k の "B スプラインの線形結合" であることを示すいくつかの方法の 1 つです。

注意: "B スプライン" という用語は、ここで "B 型のスプライン" と呼んでいるものを意味するために Computer-Aided Geometric Design (CAGD) コミュニティによって使用されてきました。その結果、残念ながら、数学者/近似理論家および CAGD に携わる人々の間での議論においては、今では常に、その用語がどの意味で使用されているかを確認しなければならなくなっています。

B スプラインの節点の多重度

ルールは次のとおりです。

節点の多重度 + 条件の多重度 = 次数

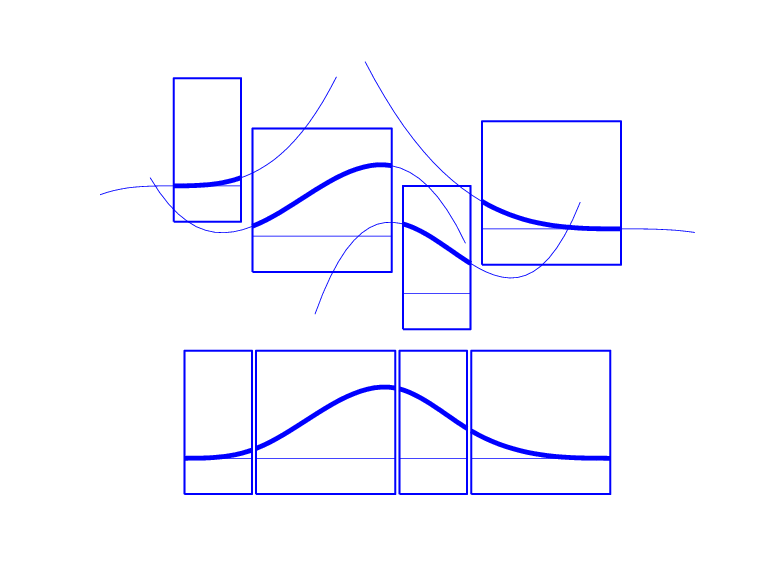
さまざまな節点の多重度をもつ特定の節点シーケンスの場合のすべての 3 次 B スプライン

たとえば、次数 3 の B スプラインの場合、簡易な節点は 2 つの平滑性条件、つまり、関数の連続性と 1 階微分を意味します。これに対して、二重節点では 1 つの平滑性条件、つまり、連続性のみが課されます。三重節点では平滑性条件が課されず、関数が不連続でも構いません。

さまざまな節点の多重度をもつ特定の節点シーケンスの場合のすべての 3 次 B スプラインは、ある未知の節点シーケンス t の場合のすべての 3 次 B スプラインの図を示しています。ブレークは垂直線で示されています。ブレークごとに、節点シーケンス (1,2,1,1,3) の多重度と、各 B スプラインの節点としての多重度の判別を試みます。たとえば、2 番目のブレークは多重度 2 ですが、3 番目の B スプラインは多重度が 1 しかないように見え、最後の 2 つの B スプラインではまったくない、つまり、多重度 0 のように見えます。示されている B スプラインの 1 つのみで、すべての節点が簡易である点に注意してください。この 1 つのみが、3 つの異なる非自明の多項式区分を持っています。また、節点の節点シーケンスの多重度は、その節点で非ゼロ部分が開始または終了する B スプラインの数によって識別できることにも注意してください。図は次の MATLAB^® ステートメントによって生成されています。ここでは、このツールボックスの spcol コマンドを使用して、細かい間隔 x でこれらの B スプラインすべての関数値を生成しています。

t=[0,1,1,3,4,6,6,6]; x=linspace(-1,7,81); 
c=spcol(t,3,x);[l,m]=size(c); 
c=c+ones(l,1)*[0:m-1]; 
axis([-1 7 0 m]); hold on 
for tt=t, plot([tt tt],[0 m],'-'), end 
plot(x,c,'linew',2), hold off, axis off

詳細な例は、例「B 型スプラインの作成と操作」に記載されています。また、GUI bspligui を使用して、B スプラインの節点への依存度を実験的に調べることもできます。

B 型向けの節点の選択

ルール "節点の多重度 + 条件の多重度 = 次数" は、B 型スプラインの近似のための節点シーケンスの選択処理において次の結果をもたらします。スプライン s は、次数が k、基本区間が [a..b] であり、内部ブレーク ξ₂< ·· ·<ξ_l をもつとします。さらに、ξ_i で、スプラインは μ_i 個の平滑性条件を満たすと仮定します。つまり、次のようになります。

$$\begin{array}{ccc}jum{p}_{{\xi }_i}{D}^{j}s:=D^{j}s\left({\xi }_{i+}\right)-D^{j}s\left({\xi }_{i-}\right)=0,& 0\le j<{\mu }_i,& i=2,\mathrm{...},l\end{array}$$

すると、適切な節点シーケンス t には、ブレーク ξ_i が正確に k – μ_i 回 (i=2,...,l) 含まれます。さらに、基本期間の 2 つの端点 a と b が正確に k 回含まれます。最後の要件は緩和できますが、基準となっています。このように選択すると、節点シーケンス t の一部の節点をもつ次数 k の B スプラインの重み付け和として説明されるプロパティを備えた各スプライン s を記述する方法は 1 つのみとなります。これが "B スプライン" の B の理由です。B スプラインは Schoenberg の用語では、"basic (基本)" スプラインだからです。

たとえば、B 型の 3 次スプラインを区間 [1 .. 3] で、1.5、1.8、2.6 という内部ブレークと 2 つの連続微分をもたせて生成する場合は、以下が適切な節点シーケンスとなります。

t = [1, 1, 1, 1, 1.5, 1.8, 2.6, 3, 3, 3, 3];

これは、augknt([1, 1.5, 1.8, 2.6, 3], 4) で提供されます。代わりに 1.8 で角を許可する、つまり、1 階微分でジャンプを可能にする場合は、節点 1.8 を三重にします。つまり、以下を使用します。

t = [1, 1, 1, 1, 1.5, 1.8, 1.8, 1.8, 2.6, 3, 3, 3, 3];

これは、次のステートメント によって与えられます。

t = augknt([1, 1.5, 1.8, 2.6, 3], 4, [1, 3, 1] );

関連するトピック

• B 型スプラインの作成と操作